Illustrative Math Alignment: Grade 6 Unit 7
Rational Numbers
Lesson 16: Common Factors
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Interactive Math Game--Factor Tree | Interactive Math Game--Factor Tree
Find the factors of the numbers in the Christmas wreath. The possible factors are on the ornaments in the tree. Click on the right factor and earn 5 points. Click on the wrong number and lose two points. Practice your factoring skills and have fun! This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions |
|
Interactive Math Game--Easter Egg (Factor) Hunt | Interactive Math Game | Easter Egg (Factor) Hunt
In this Easter Egg hunt, students find the factors of a given number from a group of eggs with numbers on them. —PRESS PREVIEW TO PLAY THE GAME— This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link.Note: The download is the teacher's guide. Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Division Expressions and Equations and Numerical Expressions |
|
|
Interactive Math Game--Easter Egg (Factor) Hunt | Interactive Math Game | Easter Egg (Factor) Hunt
In this Easter Egg hunt, students find the factors of a given number from a group of eggs with numbers on them. —PRESS PREVIEW TO PLAY THE GAME— This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link.Note: The download is the teacher's guide. Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Division Expressions and Equations and Numerical Expressions |
|
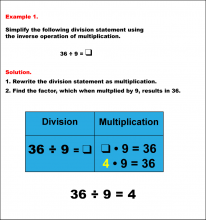
Math Example--Arithmetic--Division and Unknown Factors: Example 1 | Math Example--Arithmetic--Division and Unknown Factors: Example 1TopicArithmetic DescriptionSimplify 36 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 1 | Math Example--Arithmetic--Division and Unknown Factors: Example 1TopicArithmetic DescriptionSimplify 36 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
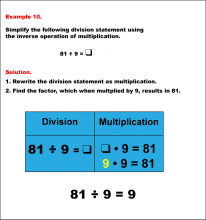
Math Example--Arithmetic--Division and Unknown Factors: Example 10 | Math Example--Arithmetic--Division and Unknown Factors: Example 10TopicArithmetic DescriptionSimplify 81 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 10 | Math Example--Arithmetic--Division and Unknown Factors: Example 10TopicArithmetic DescriptionSimplify 81 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
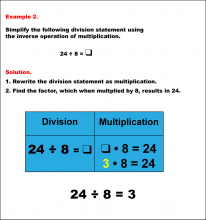
Math Example--Arithmetic--Division and Unknown Factors: Example 2 | Math Example--Arithmetic--Division and Unknown Factors: Example 2TopicArithmetic DescriptionSimplify 24 ÷ 8 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 2 | Math Example--Arithmetic--Division and Unknown Factors: Example 2TopicArithmetic DescriptionSimplify 24 ÷ 8 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
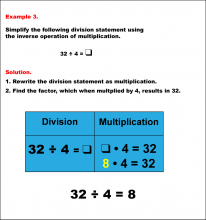
Math Example--Arithmetic--Division and Unknown Factors: Example 3 | Math Example--Arithmetic--Division and Unknown Factors: Example 3TopicArithmetic DescriptionSimplify 32 ÷ 4 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 3 | Math Example--Arithmetic--Division and Unknown Factors: Example 3TopicArithmetic DescriptionSimplify 32 ÷ 4 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
Math Example--Arithmetic--Division and Unknown Factors: Example 4 | Math Example--Arithmetic--Division and Unknown Factors: Example 4TopicArithmetic DescriptionSimplify 42 ÷ 7 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 4 | Math Example--Arithmetic--Division and Unknown Factors: Example 4TopicArithmetic DescriptionSimplify 42 ÷ 7 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
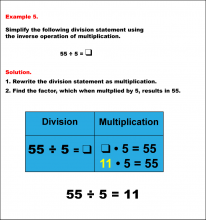
Math Example--Arithmetic--Division and Unknown Factors: Example 5 | Math Example--Arithmetic--Division and Unknown Factors: Example 5TopicArithmetic DescriptionSimplify 55 ÷ 5 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 5 | Math Example--Arithmetic--Division and Unknown Factors: Example 5TopicArithmetic DescriptionSimplify 55 ÷ 5 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
Math Example--Arithmetic--Division and Unknown Factors: Example 6 | Math Example--Arithmetic--Division and Unknown Factors: Example 6TopicArithmetic DescriptionSimplify 49 ÷ 7 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 6 | Math Example--Arithmetic--Division and Unknown Factors: Example 6TopicArithmetic DescriptionSimplify 49 ÷ 7 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
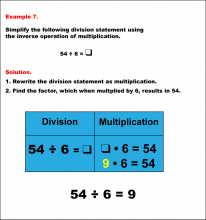
Math Example--Arithmetic--Division and Unknown Factors: Example 7 | Math Example--Arithmetic--Division and Unknown Factors: Example 7TopicArithmetic DescriptionSimplify 54 ÷ 6 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 7 | Math Example--Arithmetic--Division and Unknown Factors: Example 7TopicArithmetic DescriptionSimplify 54 ÷ 6 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
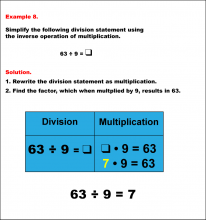
Math Example--Arithmetic--Division and Unknown Factors: Example 8 | Math Example--Arithmetic--Division and Unknown Factors: Example 8TopicArithmetic DescriptionSimplify 63 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 8 | Math Example--Arithmetic--Division and Unknown Factors: Example 8TopicArithmetic DescriptionSimplify 63 ÷ 9 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
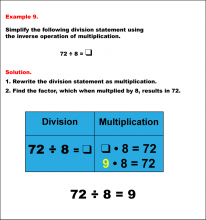
Math Example--Arithmetic--Division and Unknown Factors: Example 9 | Math Example--Arithmetic--Division and Unknown Factors: Example 9TopicArithmetic DescriptionSimplify 72 ÷ 8 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
|
Math Example--Arithmetic--Division and Unknown Factors: Example 9 | Math Example--Arithmetic--Division and Unknown Factors: Example 9TopicArithmetic DescriptionSimplify 72 ÷ 8 by using the inverse operation of multiplication. The example illustrates the method of column multiplication. The caption explains the process step-by-step, emphasizing the sequential multiplication and any necessary regrouping. In general, column multiplication is a foundational arithmetic skill that develops a student's ability to handle larger numbers systematically. Examples in this collection present varied scenarios, building confidence through exposure to different configurations of numbers. |
Division Facts and Multiplication Facts |
|
Math Example--Combinatorics--Factorial Expressions: Example 1 | Math Example--Combinatorics--Factorial Expressions: Example 1
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Data Analysis and Combinatorics |
|
|
Math Example--Combinatorics--Factorial Expressions: Example 1 | Math Example--Combinatorics--Factorial Expressions: Example 1
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Data Analysis and Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 10 | Math Example--Combinatorics--Factorial Expressions: Example 10
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 11 | Math Example--Combinatorics--Factorial Expressions: Example 11
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 12 | Math Example--Combinatorics--Factorial Expressions: Example 12
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 13 | Math Example--Combinatorics--Factorial Expressions: Example 13
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 14 | Math Example--Combinatorics--Factorial Expressions: Example 14
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 2 | Math Example--Combinatorics--Factorial Expressions: Example 2
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 3 | Math Example--Combinatorics--Factorial Expressions: Example 3
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 4 | Math Example--Combinatorics--Factorial Expressions: Example 4
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 5 | Math Example--Combinatorics--Factorial Expressions: Example 5
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 6 | Math Example--Combinatorics--Factorial Expressions: Example 6
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 7 | Math Example--Combinatorics--Factorial Expressions: Example 7
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 8 | Math Example--Combinatorics--Factorial Expressions: Example 8
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Combinatorics--Factorial Expressions: Example 9 | Math Example--Combinatorics--Factorial Expressions: Example 9
This is part of a collection of math examples that focus on combinatorics and factorial expressions. |
Combinatorics |
|
Math Example--Quadratics--Factoring Quadratics: Example 1 | Factoring Quadratics: Example 1TopicQuadratics DescriptionThis example demonstrates the factoring of a simple quadratic expression in the form x² + bx + c. The factoring process involves finding two numbers that multiply to give c and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. Factoring is often the quickest and most straightforward method for solving quadratic equations when the coefficients are integers or simple fractions. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 10 | Factoring Quadratics: Example 10TopicQuadratics DescriptionThis example showcases factoring a quadratic expression in standard form where a = 1The factoring process involves finding two numbers that multiply to give c and add up to b, considering both positive and negative factors. For instance, if the expression is x² + 5x - 24, we would look for factors of -24 that add up to 5, resulting in (x + 8)(x - 3). This method is particularly useful for solving quadratic equations and understanding the nature of the roots. It demonstrates how the signs of the factors relate to the signs of the roots, enhancing students' ability to analyze quadratic functions both algebraically and graphically. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 11 | Factoring Quadratics: Example 11TopicQuadratics DescriptionThis example illustrates factoring a quadratic expression in standard form where b = 0. The factoring process remains the same: finding two numbers that multiply to give c and add up to b, but in this case they add up to 0. For example, if the expression is x² - 13x + 36, we would look for factors of 36 that add up to -13, resulting in (x - 9)(x - 4). This type of example helps students develop their factoring skills with more challenging numbers, preparing them for more complex problem-solving scenarios. It reinforces the importance of considering both positive and negative factors and strengthens algebraic manipulation skills. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 2 | Factoring Quadratics: Example 2TopicQuadratics DescriptionThis example shows the factoring of a quadratic expression of the form x2 + bx + c, which is a modified version of the standard form. This type of factoring involves finding the factors of c that also add up to b. This skill is essential for solving more complex quadratic equations and understanding the structure of quadratic expressions. It helps in identifying the roots of quadratic functions that are not in standard form, which is crucial in many applications in physics and engineering where quadratic relationships are common. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 3 | Factoring Quadratics: Example 2TopicQuadratics DescriptionThis example shows the factoring of a quadratic expression in standard form, where a = 1. This type of factoring often involves finding the factors of a•c that add up to b. This skill is essential for solving more complex quadratic equations and understanding the structure of quadratic expressions. It helps in identifying the roots of quadratic functions that are not in standard form, which is crucial in many applications in physics and engineering where quadratic relationships are common. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 4 | Factoring Quadratics: Example 4TopicQuadratics DescriptionThis example shows the factoring of a quadratic expression in standard form (ax² + bx + c), where a = 1. The factoring process involves finding two numbers that multiply to give a•c (which is simply c in this case) and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. This type of factoring is often the first step in solving quadratic equations and is essential for understanding the structure of quadratic expressions. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 5 | Factoring Quadratics: Example 4TopicQuadratics DescriptionThis example shows the factoring of a quadratic expression in standard form (ax² + bx + c), where a = 1. The factoring process involves finding two numbers that multiply to give a•c (which is simply c in this case) and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. This type of factoring is often the first step in solving quadratic equations and is essential for understanding the structure of quadratic expressions. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 6 | Factoring Quadratics: Example 6TopicQuadratics |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 7 | Factoring Quadratics: Example 7TopicQuadratics DescriptionThis example demonstrates factoring a quadratic expression in standard form where a ≠ 1, but with a negative middle term. The process still involves finding two numbers that multiply to give a•c and add up to b, but now considering negative factors. For example, if the expression is x² - x - 12, we look for factors of -12 that add up to -1, resulting in (x - 4)(x + 3). This skill is essential for solving a wide range of quadratic equations and understanding the relationship between a quadratic's factors and its roots. It also helps in visualizing how the factored form relates to the graph of the parabola, particularly its x-intercepts. |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 8 | Factoring Quadratics: Example 8TopicQuadratics |
Factoring Quadratics |
|
Math Example--Quadratics--Factoring Quadratics: Example 9 | Factoring Quadratics: Example 9TopicQuadratics DescriptionThis example demonstrates factoring a quadratic expression where in standard form where a = 1. The process still involves finding two numbers that multiply to give c and add up to b. For example, if the expression is x² - x - 12, we look for factors of -12 that add up to -1, resulting in (x - 4)(x + 3). This skill is essential for solving a wide range of quadratic equations and understanding the relationship between a quadratic's factors and its roots. It also helps in visualizing how the factored form relates to the graph of the parabola, particularly its x-intercepts. |
Factoring Quadratics |
|
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 1 | Graphs of Quadratic Functions in Factored Form--Example 1TopicQuadratics |
Graphs of Quadratic Functions |
