
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 1: Relationships between Quantities
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Equation Concepts--Transitive Property of Equality | Transitive Property of EqualityTopicEquations DefinitionThe Transitive Property of Equality states that if a = b and b = c, then a = c. DescriptionThe Transitive Property of Equality is a fundamental principle in mathematics. It states that if one quantity equals a second quantity, and the second quantity equals a third, then the first and third quantities are equal. For example, if x = y and y = z then x = z This property is used to justify steps in solving equations and proving mathematical statements. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--True Equation | True EquationTopicEquations DefinitionA true equation is an equation that holds true for the given values of the variable(s). DescriptionA true equation is an equation that is valid for specific values of the variable(s). For example, the equation 2 + 3 = 5 is true because both sides are equal. Identifying true equations is important in verifying the correctness of mathematical statements. In real-world applications, recognizing true equations helps in ensuring the accuracy of mathematical models and solutions. Understanding true equations helps students develop critical thinking and analytical skills. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Two-Step Equation | Two-Step EquationTopicEquations DefinitionA two-step equation requires two operations to solve. DescriptionTwo-step equations involve performing two operations to isolate the variable. For example, solving 2x + 3 = 7 requires subtracting 3 from both sides and then dividing by 2 to find x = 2. These equations are common in algebra and require a systematic approach to solve. In real-world applications, two-step equations are used in problem-solving scenarios such as calculating costs or determining measurements. Understanding how to solve two-step equations helps students develop critical thinking and problem-solving skills. |
Solving Two-Step Equations |

|
Definition--Equation Concepts--Variable Expression | Variable ExpressionTopicEquations DefinitionA variable expression is a mathematical phrase involving variables, numbers, and operation symbols. DescriptionVariable expressions consist of variables, numbers, and operations such as addition, subtraction, multiplication, and division. For example, 3x + 4 is a variable expression. These expressions are used to represent quantities and relationships in algebra. |
Variable Expressions |
|
Definition--Equation Concepts--Visual Models for Equations | Visual Models for EquationsTopicEquations DefinitionVisual models for equations use graphical representations to illustrate the relationships between variables. DescriptionVisual models for equations include graphs, charts, and diagrams that represent the relationships between variables. For example, a graph of the equation y = 2x + 3 shows a straight line with a slope of 2 and a y-intercept of 3. These models help in understanding and interpreting equations. |
Applications of Equations and Inequalities |

|
INSTRUCTIONAL RESOURCE: Tutorial: Visual Models for Equations | INSTRUCTIONAL RESOURCE: Tutorial: Visual Models for Equations
An equation shows a relationship between two quantities. The download is a PDF. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Algebra Tiles--Expressions and Equations and Applications of Equations and Inequalities |

|
INSTRUCTIONAL RESOURCE: Tutorial: What Is an Equation? | INSTRUCTIONAL RESOURCE: Tutorial: What Is an Equation?
An equation shows a relationship between two quantities. Note: The download is a PDF. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Equations and Inequalities and Variables and Unknowns |

|
Interactive Math Game: Equation Sort 2 | Interactive Math Game: Equation Sort 2
Use this math game to review one-step equations. Students are shown four equations and are asked to correctly label the equation with drag-and-drop. The game provides feedback. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities and Solving One-Step Equations |

|
Interactive Math Game: Equation Sort 3 | Interactive Math Game: Equation Sort 3
Use this math game to review two-step equations. Students are shown four equations and are asked to correctly label the equation with drag-and-drop. The game provides feedback. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Solving Two-Step Equations |

|
Techniques for Solving Equations | INSTRUCTIONAL RESOURCE: Tutorial: Techniques for Solving Equations
In this tutorial, students are shown the process of solving equations. In particular, they look at the properties of equality that allow for the manipulation of equations in order to arrive at a solution. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Equations and Inequalities |

|
Video Definition 1--Equation Concepts--"Not Equal To" Sign | Video Definition 1--Equation Concepts--"Not Equal To" Sign
TopicEquations DescriptionThe Not Equal To Sign (≠) indicates two expressions are not equal, forming an inequation. For example, 2 + 1 ≠ 4 and x + 3 ≠ x are inequations. This term builds on equality concepts by introducing inequalities, critical for exploring a broader range of mathematical statements. |
Numerical and Algebraic Expressions |

|
Video Definition 10--Equation Concepts--Equation | Video Definition 10--Equation Concepts--Equation
TopicEquations DescriptionAn Equation is a mathematical statement that says two expressions are equal to each other. Equations can be true or false, as shown in examples like 1 + 1 = 2 (true) and 1 + 2 = 4 (false). This term introduces the concept of equality and sets the foundation for understanding other types of equations. |
Applications of Equations and Inequalities |

|
Video Definition 11--Equation Concepts--Equations in One Variable | Video Definition 11--Equation Concepts--Equations in One Variable
TopicEquations DescriptionAn Equation in One Variable has an unknown represented by a single variable. Examples include 2 + 3x = 5 and (x + 2)^2 = 25. This term focuses on single-variable equations, forming a basis for solving and understanding algebraic structures. |
Applications of Equations and Inequalities |

|
Video Definition 12--Equation Concepts--Equations in Two Variables | Video Definition 12--Equation Concepts--Equations in Two Variables
TopicEquations DescriptionEquations in Two Variables. A two-variable equation shows a relationship between two variables. Examples include y = 3x + 5, x2 + y2 = 25, and xy = 5, highlighting equations that can be graphed in a coordinate system. This builds on the idea of variables in equations and introduces the concept of relationships between variables, applicable in graphing and real-world modeling. |
Applications of Equations and Inequalities |

|
Video Definition 13--Equation Concepts--Equivalent Equations | Video Definition 13--Equation Concepts--Equivalent Equations
TopicEquations DescriptionEquivalent Equations result from changing an equation while maintaining equality, often by performing the same operation on both sides. For example, x - 3 = 5 becomes x = 8 after adding 3 to both sides. This term demonstrates how equations can be manipulated without altering their solution, a key concept in solving equations. |
Applications of Equations and Inequalities |

|
Video Definition 14--Equation Concepts--False Equation | Video Definition 14--Equation Concepts--False Equation
TopicEquations DescriptionA False Equation is mathematically inaccurate. For example, 2 + 1 = 4 is false, and x + 3 = x has no solution, as no value of x satisfies the equation. This term contrasts true equations and emphasizes the need to verify solutions, highlighting logical consistency in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 15--Equation Concepts--Identity Equation | Video Definition 15--Equation Concepts--Identity Equation
TopicEquations DescriptionAn Identity Equation is always true for all variable values. Examples include x = x and (x + 1)2 = x2 + 2x + 1. Identity equations often use the symbol ≡ to indicate their universal truth. This term introduces a special class of equations, linking algebraic manipulation and properties of equivalence. |
Applications of Equations and Inequalities |

|
Video Definition 16--Equation Concepts--Inequation | Video Definition 16--Equation Concepts--Inequation
TopicEquations DescriptionAn Inequation is a mathematical statement that shows two expressions are not equal, as in 2 + 1 ≠ 4 or x + 3 ≥ 0, which includes inequalities. This term broadens the discussion to include inequalities, expanding the types of relationships between expressions. |
Inequalities |

|
Video Definition 17--Equation Concepts--Isolating the Variable | Video Definition 17--Equation Concepts--Isolating the Variable
TopicEquations DescriptionIsolating the Variable refers to the process of solving an equation by focusing on and isolating the variable of interest. For example, x + 3 = 5 becomes x = 2 by subtracting 3 from both sides. This term highlights a key step in solving equations, emphasizing strategies for simplifying equations to find solutions. |
Variables and Unknowns |

|
Video Definition 18--Equation Concepts--Left Side of the Equation | Video Definition 18--Equation Concepts--Left Side of the Equation
TopicEquations DescriptionThe Left Side of the Equation is the expression on the left of the equals sign. For example, in 2x + 3 = x - 5, the left side is 2x + 3. This term provides clarity in identifying components of equations, aiding in understanding structure and solving strategies. |
Applications of Equations and Inequalities |

|
Video Definition 19--Equation Concepts--Linear Equation | Video Definition 19--Equation Concepts--Linear Equation
TopicEquations DescriptionA Linear Equation is an equation where variables have an exponent of 1. Examples include x + 2 = 7, 2x + 3y = 4, and y = -2x + 10. Graphs of two-variable linear equations are straight lines. This term introduces a fundamental class of equations with specific properties, crucial for algebra and graphing. |
Applications of Linear Functions |

|
Video Definition 2--Equation Concepts--Addition Property of Equality | Video Definition 2--Equation Concepts--Addition Property of Equality
TopicEquations DescriptionThe Addition Property of Equality allows the addition of the same quantity to each side of an equation while maintaining equality. For example, if a = b, then a + c = b + c. This concept ensures equations can be manipulated while preserving their equality, demonstrated by solving x - 2 = 3 as x = 5 after adding 2 to both sides. This term introduces the basic manipulation of equations, forming the foundation for solving linear equations and maintaining equality. |
Applications of Equations and Inequalities |

|
Video Definition 20--Equation Concepts--Literal Equation | Video Definition 20--Equation Concepts--Literal Equation
TopicEquations DescriptionA Literal Equation includes more than one variable and often represents formulas, such as A = πr2, V = l*w*h, and SA = 2πr*h + 2πr2. This term connects to real-world applications and highlights the versatility of equations in representing formulas and relationships. |
Applications of Equations and Inequalities |

|
Video Definition 21--Equation Concepts--Multi-Step Equation | Video Definition 21--Equation Concepts--Multi-Step Equation
TopicEquations DescriptionA Multi-Step Equation involves more than two mathematical operations to solve. For example, 4x + 2 = 2x + 8 simplifies to x = 3 after subtraction and division steps. This term emphasizes solving more complex equations, showing sequential steps and reinforcing logical progression in algebra. |
Solving Multistep Equations |

|
Video Definition 22--Equation Concepts--Multiplication Property of Equality | Video Definition 22--Equation Concepts--Multiplication Property of Equality
TopicEquations DescriptionThe Multiplication Property of Equality allows multiplication by the same non-zero quantity on both sides of an equation, maintaining equality. For example, if a = b, then a * c = b * c. Solving x/2 = 3 yields x = 6 by multiplying both sides by 2. This term builds on equality principles and demonstrates another method for solving equations by manipulating terms. |
Applications of Equations and Inequalities |

|
Video Definition 23--Equation Concepts--Nonlinear Equation | Video Definition 23--Equation Concepts--Nonlinear Equation
TopicEquations DescriptionA Non-Linear Equation includes non-linear terms such as polynomials of degree 2 or higher, exponential, logarithmic, or trigonometric terms. Examples include y = x2 - 4x + 5 and y = sin(x). This term expands understanding beyond linear relationships, introducing diverse mathematical models and their applications. |
Applications of Equations and Inequalities |

|
Video Definition 24--Equation Concepts--Numerical Expression | Video Definition 24--Equation Concepts--Numerical Expression
TopicEquations DescriptionA Numerical Expression consists of numbers and operations without variables. Examples include 2 + 3 = 5 and 2(4 + 3) = 14. This term highlights fundamental operations, foundational for understanding and solving equations. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Numerical Expressions |

|
Video Definition 25--Equation Concepts--One-Step Equation | Video Definition 25--Equation Concepts--One-Step Equation
TopicEquations DescriptionA One-Step Equation involves a single mathematical operation to solve. For example, x + 2 = 3 simplifies to x = 1 by subtraction. This term introduces the simplest form of equations, essential for beginners to build confidence and understanding in solving. |
Solving One-Step Equations |

|
Video Definition 26--Equation Concepts--Polynomial Equation | Video Definition 26--Equation Concepts--Polynomial Equation
TopicEquations DescriptionA Polynomial Equation consists of a polynomial expression equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. This term defines a key class of equations, critical for algebra and calculus studies. |
Polynomial Functions and Equations |

|
Video Definition 27--Equation Concepts--Quadratic Equation | Video Definition 27--Equation Concepts--Quadratic Equation
TopicEquations DescriptionA Quadratic Equation is a polynomial of degree 2. Examples include x2 - 2 = 23 and 2x2 + 3x + 2 = 0. Graphs of such equations are parabolas. This term extends understanding of polynomial equations, connecting algebra to geometry through parabolas. |
Quadratic Equations and Functions |

|
Video Definition 28--Equation Concepts--Reflexive Property of Equality | Video Definition 28--Equation Concepts--Reflexive Property of Equality
TopicEquations DescriptionThe Reflexive Property of Equality states that any quantity is equal to itself. Examples include 5 = 5 and x + 2 = x + 2. This term reinforces the foundational principle of equality, essential for logical reasoning in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 29--Equation Concepts--Right Side of the Equation | Video Definition 29--Equation Concepts--Right Side of the Equation
TopicEquations DescriptionRight Side of the Equation. The expression to the right side of the equals sign in an equation. 2x + 3 = x - 5 (right side highlighted) The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 3--Equation Concepts--Algebraic Equation | Video Definition 3--Equation Concepts--Algebraic Equation
TopicEquations DescriptionAn Algebraic Equation is another term for a polynomial equation, represented as a sum of terms equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. It highlights the structure of polynomial equations using constants, variables, and powers. This term connects to the topic by defining the types of equations learners encounter when solving or simplifying expressions. |
Applications of Equations and Inequalities |
|
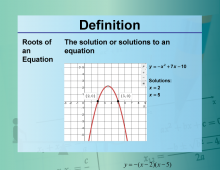
Video Definition 30--Equation Concepts--Roots of an Equation | Video Definition 30--Equation Concepts--Roots of an Equation
TopicEquations DescriptionRoots of an Equation. The solution or solutions to an equation. y = -x2 + 7x - 10; solutions: x = 2, x = 5 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 31--Equation Concepts--Solution | Video Definition 31--Equation Concepts--Solution
TopicEquations DescriptionSolution. A value for the unknown that turns a conditional equation into a true equation. For example, x = 5 is a solution to x + 2 = 7 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 32--Equation Concepts--Solving an Equation | Video Definition 32--Equation Concepts--Solving an Equation
TopicEquations DescriptionSolving an Equation. The process of finding the value(s) for a variable that result in a true equation. For example, x + 2 = 3 has a solution of x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 33--Equation Concepts--Subtraction Property of Equality | Video Definition 33--Equation Concepts--Subtraction Property of Equality
TopicEquations DescriptionSubtraction Property of Equality. The property that allows the subtraction of the same quantity from each side of an equation while maintaining the equality. For example, x + 2 = 3 becomes x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 34--Equation Concepts--Symmetric Property of Equality | Video Definition 34--Equation Concepts--Symmetric Property of Equality
TopicEquations DescriptionSymmetric Property of Equality. The property that states that an equation can be written two ways, with both sides interchanged. If a = b, then b = a. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 35--Equation Concepts--The Unknown | Video Definition 35--Equation Concepts--The Unknown
TopicEquations DescriptionThe Unknown. In a conditional equation, the variable is also referred to as the unknown. 3x = 12, where x is the unknown The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Variables and Unknowns |

|
Video Definition 36--Equation Concepts--Transitive Property of Equality | Video Definition 36--Equation Concepts--Transitive Property of Equality
TopicEquations DescriptionTransitive Property of Equality. The property that states that two quantities equal to a third quantity are equal to each other. If a = b and b = c, then a = c The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 37--Equation Concepts--True Equation | Video Definition 37--Equation Concepts--True Equation
TopicEquations DescriptionTrue Equation. A mathematically accurate equation. If variables are involved, the true equation is for the values of the variable that make the equation true. Examples: 2 + 1 = 3; (2 + 3)2 = 25; x + 3 = 9 for x = 6 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 38--Equation Concepts--Two-Step Equation | Video Definition 38--Equation Concepts--Two-Step Equation
TopicEquations DescriptionTwo-Step Equation. A two-step equation is an equation that involves two mathematical operations to solve. The example given is 2x + 2 = 8, where the first operation is subtraction, leading to 2x = 6, followed by division to solve for x = 3. This concept extends the understanding of solving equations by introducing a sequence of operations, crucial for solving more complex equations. |
Solving Two-Step Equations |

|
Video Definition 39--Equation Concepts--Variable Expression | Video Definition 39--Equation Concepts--Variable Expression
TopicEquations DescriptionVariable Expression. A variable expression is made up of numbers, operations, and variables. Examples include 2x + 3 = 5 (expression on the left), 4 = 3x + 7 (expression on the right), and 4x + 3 = x - 5 (expressions on both sides). This connects variables to equations and highlights their role in forming relationships within mathematical contexts. |
Variable Expressions |

|
Video Definition 4--Equation Concepts--Algebraic Expression | Video Definition 4--Equation Concepts--Algebraic Expression
TopicEquations DescriptionAn Algebraic Expression consists of numbers, operations, and variables. Unlike equations, expressions may not have an equality. Examples include 2x + 3, 4 = 3x + 7, and 4x + 3 = x - 5, demonstrating their versatility in representing mathematical relationships. This term distinguishes between expressions and equations, forming the basis for manipulating algebraic forms before solving equations. |
Numerical and Algebraic Expressions |

|
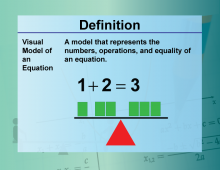
Video Definition 40--Equation Concepts--Visual Models for Equations | Video Definition 40--Equation Concepts--Visual Models for Equations
TopicEquations DescriptionVisual Model of an Equation. A visual model of an equation represents the numbers, operations, and equality using visuals. The example shows 1 + 2 = 3 with blocks illustrating the balance of the equation. This visual approach reinforces the foundational concept of equality and provides an intuitive way to understand equations, especially for visual learners. |
Applications of Equations and Inequalities |

|
Video Definition 41--Equation Concepts--Approximately Equal To | Video Definition 41--Equation Concepts--Approximately Equal To
TopicEquations DescriptionThe Approximately Equal To Sign (≈) indicates that two expressions are close in value but not equal. Examples include estimating sums (58 + 49 ≈ 100), square roots (√50 ≈ 7), and function values (f(x) ≈ 25). This term relates to the topic by introducing estimation techniques, valuable for checking solutions or simplifying problems. |
Applications of Equations and Inequalities |

|
Video Definition 42--Equation Concepts--Proportional To | Video Definition 42--Equation Concepts--Proportional To
TopicEquations DescriptionProportional To indicates a linear relationship between two variables. For example, distance (d) is proportional to time (t), written as d ∝ t. This term links linear equations to real-world relationships, reinforcing practical applications of mathematical concepts. |
Applications of Equations and Inequalities |
|
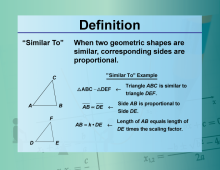
Video Definition 43--Equation Concepts--Similar To | Video Definition 43--Equation Concepts--Similar To
TopicEquations DescriptionSimilar To. When two geometric shapes are similar, corresponding sides are proportional. ΔABC ~ ΔDEF; AB ∝ DE The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 44--Equation Concepts--Congruent To | Video Definition 44--Equation Concepts--Congruent To
TopicEquations DescriptionCongruent To signifies that two geometric shapes are congruent, meaning their corresponding sides and angles are equal. For example, triangles ABC and DEF are congruent, so side AB equals side DE. This term introduces geometric equality, tying equations to geometric properties and congruence criteria. |
Applications of Equations and Inequalities |

|
Video Definition 5--Equation Concepts--Assigning Values to Variables | Video Definition 5--Equation Concepts--Assigning Values to Variables
TopicEquations DescriptionAssigning Values to Variables involves assigning a numerical value to a variable for evaluating functions. For instance, let x = 3 in f(x) = 2x + 8 yields f(3) = 14. This term supports understanding how to evaluate equations and functions by substituting values, a key step in problem-solving. |
Variable Expressions |