
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 9: Dealing with Negative Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Video Definition 27--Rationals and Radicals--Radical Equations (Spanish Audio) | Video Definition 27--Rationals and Radicals--Radical Equations (Spanish Audio)
TopicRationals and Radicals DescriptionRadical equations involve solving expressions with radicals by raising both sides to a power. An example solves √(x + 2) = x, resulting in x = 2 or x = -1. This term demonstrates how radicals can be manipulated algebraically to find solutions, integrating concepts of nth roots and square roots. This video includes Spanish audio and can be used with multilingual learners. |
Radical Functions and Equations |

|
Video Definition 28--Equation Concepts--Reflexive Property of Equality | Video Definition 28--Equation Concepts--Reflexive Property of Equality
TopicEquations DescriptionThe Reflexive Property of Equality states that any quantity is equal to itself. Examples include 5 = 5 and x + 2 = x + 2. This term reinforces the foundational principle of equality, essential for logical reasoning in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 29--Equation Concepts--Right Side of the Equation | Video Definition 29--Equation Concepts--Right Side of the Equation
TopicEquations DescriptionRight Side of the Equation. The expression to the right side of the equals sign in an equation. 2x + 3 = x - 5 (right side highlighted) The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 3--Equation Concepts--Algebraic Equation | Video Definition 3--Equation Concepts--Algebraic Equation
TopicEquations DescriptionAn Algebraic Equation is another term for a polynomial equation, represented as a sum of terms equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. It highlights the structure of polynomial equations using constants, variables, and powers. This term connects to the topic by defining the types of equations learners encounter when solving or simplifying expressions. |
Applications of Equations and Inequalities |
|
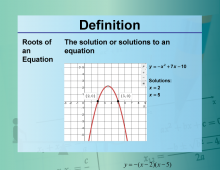
Video Definition 30--Equation Concepts--Roots of an Equation | Video Definition 30--Equation Concepts--Roots of an Equation
TopicEquations DescriptionRoots of an Equation. The solution or solutions to an equation. y = -x2 + 7x - 10; solutions: x = 2, x = 5 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 31--Equation Concepts--Solution | Video Definition 31--Equation Concepts--Solution
TopicEquations DescriptionSolution. A value for the unknown that turns a conditional equation into a true equation. For example, x = 5 is a solution to x + 2 = 7 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 32--Equation Concepts--Solving an Equation | Video Definition 32--Equation Concepts--Solving an Equation
TopicEquations DescriptionSolving an Equation. The process of finding the value(s) for a variable that result in a true equation. For example, x + 2 = 3 has a solution of x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 33--Equation Concepts--Subtraction Property of Equality | Video Definition 33--Equation Concepts--Subtraction Property of Equality
TopicEquations DescriptionSubtraction Property of Equality. The property that allows the subtraction of the same quantity from each side of an equation while maintaining the equality. For example, x + 2 = 3 becomes x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 33--Rationals and Radicals--Rational Equations | Video Definition 33--Rationals and Radicals--Rational Equations
TopicRationals and Radicals DescriptionRational Equations are equations involving fractions where both sides include variables. These often involve steps to solve for variables, like x in (2x + 6) / (x - 3) = 5. Extends the use of fractions by incorporating variables, creating a bridge between fractions and algebra. |
Rational Functions and Equations |

|
Video Definition 33--Rationals and Radicals--Rational Equations (Spanish Audio) | Video Definition 33--Rationals and Radicals--Rational Equations (Spanish Audio)
TopicRationals and Radicals DescriptionRational Equations are equations involving fractions where both sides include variables. These often involve steps to solve for variables, like x in (2x + 6) / (x - 3) = 5. Extends the use of fractions by incorporating variables, creating a bridge between fractions and algebra. This video includes Spanish audio and can be used with multilingual learners. |
Rational Functions and Equations |

|
Video Definition 34--Equation Concepts--Symmetric Property of Equality | Video Definition 34--Equation Concepts--Symmetric Property of Equality
TopicEquations DescriptionSymmetric Property of Equality. The property that states that an equation can be written two ways, with both sides interchanged. If a = b, then b = a. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 35--Equation Concepts--The Unknown | Video Definition 35--Equation Concepts--The Unknown
TopicEquations DescriptionThe Unknown. In a conditional equation, the variable is also referred to as the unknown. 3x = 12, where x is the unknown The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Variables and Unknowns |

|
Video Definition 36--Equation Concepts--Transitive Property of Equality | Video Definition 36--Equation Concepts--Transitive Property of Equality
TopicEquations DescriptionTransitive Property of Equality. The property that states that two quantities equal to a third quantity are equal to each other. If a = b and b = c, then a = c The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 37--Equation Concepts--True Equation | Video Definition 37--Equation Concepts--True Equation
TopicEquations DescriptionTrue Equation. A mathematically accurate equation. If variables are involved, the true equation is for the values of the variable that make the equation true. Examples: 2 + 1 = 3; (2 + 3)2 = 25; x + 3 = 9 for x = 6 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 38--Equation Concepts--Two-Step Equation | Video Definition 38--Equation Concepts--Two-Step Equation
TopicEquations DescriptionTwo-Step Equation. A two-step equation is an equation that involves two mathematical operations to solve. The example given is 2x + 2 = 8, where the first operation is subtraction, leading to 2x = 6, followed by division to solve for x = 3. This concept extends the understanding of solving equations by introducing a sequence of operations, crucial for solving more complex equations. |
Solving Two-Step Equations |

|
Video Definition 39--Equation Concepts--Variable Expression | Video Definition 39--Equation Concepts--Variable Expression
TopicEquations DescriptionVariable Expression. A variable expression is made up of numbers, operations, and variables. Examples include 2x + 3 = 5 (expression on the left), 4 = 3x + 7 (expression on the right), and 4x + 3 = x - 5 (expressions on both sides). This connects variables to equations and highlights their role in forming relationships within mathematical contexts. |
Variable Expressions |

|
Video Definition 4--Equation Concepts--Algebraic Expression | Video Definition 4--Equation Concepts--Algebraic Expression
TopicEquations DescriptionAn Algebraic Expression consists of numbers, operations, and variables. Unlike equations, expressions may not have an equality. Examples include 2x + 3, 4 = 3x + 7, and 4x + 3 = x - 5, demonstrating their versatility in representing mathematical relationships. This term distinguishes between expressions and equations, forming the basis for manipulating algebraic forms before solving equations. |
Numerical and Algebraic Expressions |
|
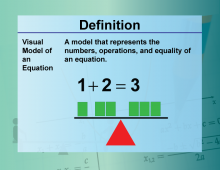
Video Definition 40--Equation Concepts--Visual Models for Equations | Video Definition 40--Equation Concepts--Visual Models for Equations
TopicEquations DescriptionVisual Model of an Equation. A visual model of an equation represents the numbers, operations, and equality using visuals. The example shows 1 + 2 = 3 with blocks illustrating the balance of the equation. This visual approach reinforces the foundational concept of equality and provides an intuitive way to understand equations, especially for visual learners. |
Applications of Equations and Inequalities |

|
Video Definition 41--Equation Concepts--Approximately Equal To | Video Definition 41--Equation Concepts--Approximately Equal To
TopicEquations DescriptionThe Approximately Equal To Sign (≈) indicates that two expressions are close in value but not equal. Examples include estimating sums (58 + 49 ≈ 100), square roots (√50 ≈ 7), and function values (f(x) ≈ 25). This term relates to the topic by introducing estimation techniques, valuable for checking solutions or simplifying problems. |
Applications of Equations and Inequalities |

|
Video Definition 42--Equation Concepts--Proportional To | Video Definition 42--Equation Concepts--Proportional To
TopicEquations DescriptionProportional To indicates a linear relationship between two variables. For example, distance (d) is proportional to time (t), written as d ∝ t. This term links linear equations to real-world relationships, reinforcing practical applications of mathematical concepts. |
Applications of Equations and Inequalities |
|
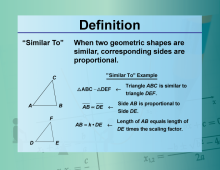
Video Definition 43--Equation Concepts--Similar To | Video Definition 43--Equation Concepts--Similar To
TopicEquations DescriptionSimilar To. When two geometric shapes are similar, corresponding sides are proportional. ΔABC ~ ΔDEF; AB ∝ DE The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 44--Equation Concepts--Congruent To | Video Definition 44--Equation Concepts--Congruent To
TopicEquations DescriptionCongruent To signifies that two geometric shapes are congruent, meaning their corresponding sides and angles are equal. For example, triangles ABC and DEF are congruent, so side AB equals side DE. This term introduces geometric equality, tying equations to geometric properties and congruence criteria. |
Applications of Equations and Inequalities |

|
Video Definition 5--Equation Concepts--Assigning Values to Variables | Video Definition 5--Equation Concepts--Assigning Values to Variables
TopicEquations DescriptionAssigning Values to Variables involves assigning a numerical value to a variable for evaluating functions. For instance, let x = 3 in f(x) = 2x + 8 yields f(3) = 14. This term supports understanding how to evaluate equations and functions by substituting values, a key step in problem-solving. |
Variable Expressions |

|
Video Definition 6--Equation Concepts--Conditional Equation | Video Definition 6--Equation Concepts--Conditional Equation
TopicEquations DescriptionA Conditional Equation is true only for specific variable values. Examples include x + 1 = 4 (x = 3), x2 - 25 = 0 (x = ±5), and 2x - 5 = x + 9 (x = 14). This term supports solving equations by emphasizing that solutions depend on satisfying the given conditions. |
Applications of Equations and Inequalities |

|
Video Definition 7--Equation Concepts--Constant Term | Video Definition 7--Equation Concepts--Constant Term
TopicEquations DescriptionA Constant Term in an algebraic equation is a number without a variable. Examples include 2 in x2 + 3x + 2 = 0, -10 in x3 - 2x2 + 4x - 10 = 0, and 5 in x4 - 2x3 + 4x2 - x + 5 = 0. This term explains the role of constants in equations, crucial for identifying and isolating terms when solving equations. |
Variables and Unknowns |
|
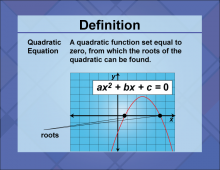
Video Definition 7--Quadratics Concepts--Quadratic Equation | Video Definition 7--Quadratics Concepts--Quadratic Equation
TopicQuadratics DescriptionQuadratic Equation: A quadratic function set equal to zero, from which the roots of the quadratic can be found. This is foundational in solving quadratic problems algebraically. Introduces the mathematical setup for finding solutions to quadratic functions. Relevance to Topic: This video series provides a deep dive into the topic of Quadratics. It explores mathematical concepts and demonstrates real-world applications to help solidify understanding. |
Quadratic Equations and Functions |

|
Video Definition 8--Equation Concepts--Division Property of Equality | Video Definition 8--Equation Concepts--Division Property of Equality
TopicEquations DescriptionThe Division Property of Equality allows division by the same non-zero quantity on both sides of an equation, maintaining equality. For example, if a = b, then a / c = b / c, where c ≠ 0. Solving 5x = 15 yields x = 3 by dividing both sides by 5. This term builds on equality principles, showing another method to isolate variables and solve equations. |
Applications of Equations and Inequalities |

|
Video Definition 9--Equation Concepts--Equality | Video Definition 9--Equation Concepts--Equality
TopicEquations DescriptionEquality refers to a mathematical statement where two expressions are equal. Examples include 1 + 2 = 3 and x + 3 = 7, where both sides represent the same value. This term defines the core concept of equations, ensuring all manipulations preserve equality to find solutions. |
Applications of Equations and Inequalities |

|
Video Definition 9--Linear Function Concepts--The Equation of a Line From Two Coordinates | Video Definition 9--Linear Function Concepts--The Equation of a Line From Two Coordinates
TopicLinear Functions DescriptionThe term is "The Equation of a Line from Two Coordinates," defined as deriving the equation of a line in slope-intercept form from two given points. The slope is calculated as m = (y2 - y1) / (x2 - x1), and the equation is written as y - y1 = m(x - x1). This term builds the connection between points on a graph and their corresponding linear equation, demonstrating practical derivations. |
Point-Slope Form |

|
Video Transcript: Algebra Applications: Systems of Equations | Video Transcript: Algebra Applications: Systems of Equations
This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, students explore various scenarios that can be explained through the use of systems of equations. Such disparate phenomena as profit and loss, secret codes, and ballistic missile shields can be explored through systems of equations. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Applications: Systems of Equations, Segment 1: Profit and Loss | Video Transcript: Algebra Applications: Systems of Equations, Segment 1: Profit and Loss
This is the transcript for the video of same title. Video contents: Profit and loss are the key measures in a business. A system of equations that includes an equation for income and one for expenses can be used to determine profit and loss. Students solve a system graphically. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Applications: Systems of Equations, Segment 2: Encryption | Video Transcript: Algebra Applications: Systems of Equations, Segment 2: Encryption
This is the transcript for the video of same title. Video contents: Secret codes and encryption are ideal examples of a system of equations. In this activity, students encrypt and decrypt a message. This is part of a collection of video transcript from the Algebra Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Applications: Systems of Equations, Segment 3: Ballistic Missiles | Video Transcript: Algebra Applications: Systems of Equations, Segment 3: Ballistic Missiles
This is the transcript for the video of same title. Video contents: A ballistic missile shield allows you to shoot incoming missiles out of the sky. Mathematically, this is an example of a linear-quadratic system. Students graph such a system and find the points of intersection between a line and a parabola. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Applications: Variables and Equations | Video Transcript: Algebra Applications: Variables and Equations
This is the transcript for the video of same title. Video contents: In this episode of Algebra Applications, two real-world explorations are developed: Biology. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder. Geology. Why do rivers meander instead of traveling in a straight line? In this segment the geological forces that account for a river??s motion are explained. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Applications: Variables and Equations, Segment 1: Introduction. | Video Transcript: Algebra Applications: Variables and Equations, Segment 1: Introduction.
This is the transcript for the video of same title. Video contents: An overview of the key topics to be covered in the video. This is part of a collection of video transcript from the Algebra Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Applications: Variables and Equations, Segment 2: Honey Production | Video Transcript: Algebra Applications: Variables and Equations, Segment 2: Honey Production
This is the transcript for the video of same title. Video contents: Honey bees not only produce a tasty treat, they also help pollinate flowering plants that provide much of the food throughout the world. So, when in 2006 bee colonies started dying out, scientists recognized a serious problem. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Applications: Variables and Equations, Segment 3: River Ratios | Video Transcript: Algebra Applications: Variables and Equations, Segment 3: River Ratios This is the transcript for the video of same title. Video contents: Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river's length to its straight-line distance tell us? In this segment the geological forces that account for a river's motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi. |
Applications of Equations and Inequalities and Applications of Ratios, Proportions, and Percents |

|
Video Transcript: Algebra Nspirations: Solving Systems of Equations | Video Transcript: Algebra Nspirations: Solving Systems of Equations
This is the transcript for the video of same title. Video contents: Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video introduces students to systems of linear equations in two or three unknowns. To solve these systems, the host illustrates a variety of methods: four involve the TI-Nspire (spreadsheet, graphs and geometry, matrices and nSolve) and two are the classic algebraic methods known as substitution and elimination, also called the linear combinations method. The video ends with a summary of the three possible types of solutions. Concepts explored: equations, linear equations, linear systems |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Nspirations: Solving Systems of Equations, 1 | Video Transcript: Algebra Nspirations: Solving Systems of Equations, Part 1
This is the transcript for the video of same title. Video contents: In this Investigation we solve a linear system. This is part of a collection of video transcript from the Algebra Nspirations video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Nspirations: Solving Systems of Equations, 2 | Video Transcript: Algebra Nspirations: Solving Systems of Equations, Part 2
This is the transcript for the video of same title. Video contents: In this Investigation we use matrices and the elimination method to solve a linear system. This is part of a collection of video transcript from the Algebra Nspirations video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Linear Systems, Matrix Operations and Solving Systems of Equations |

|
Video Transcript: Algebra Nspirations: Variables and Equations | Video Transcript: Algebra Nspirations: Variables and Equations
This is the transcript for the video of same title. Video contents: Ever since the mathematics of the Babylonians, equations have played a central role in the development of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video traces the history and evolution of equations. It explores the two principal equations encountered in an introductory algebra course -- linear and quadratic -- in an engaging way. The foundations of algebra are explored and fundamental questions about the nature of algebra are answered. In addition, problems involving linear and quadratic equations are solved using the TI-Nspire graphing calculator. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Nspirations: Variables and Equations, 1 | Video Transcript: Algebra Nspirations: Variables and Equations, Part 1
This is the transcript for the video of same title. Video contents: In this Investigation we get a historical overview of equations. This is part of a collection of video transcript from the Algebra Nspirations video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Nspirations: Variables and Equations, 2 | Video Transcript: Algebra Nspirations: Variables and Equations, Part 2
This is the transcript for the video of same title. Video contents: In this Investigation we solve linear and quadratic equations. This is part of a collection of video transcript from the Algebra Nspirations video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Equations and Inequalities |

|
Video Transcript: Algebra Tiles: Modeling Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Modeling Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Modeling Multi-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Modeling Multi-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Modeling One-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Modeling One-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Modeling Quadratic Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Modeling Quadratic Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Modeling Two-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Modeling Two-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |

|
Video Transcript: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles | Video Transcript: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles
What Are Algebra Tiles?Numerical Models |
Algebra Tiles--Expressions and Equations |