Illustrative Math Alignment: Grade 7 Unit 7

Angles, Triangles, and Prisms

Lesson 10: Drawing Triangles (Part 2)

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Definition--Triangle Concepts--Pythagorean Triples	Pythagorean Triples Topic Triangles Definition Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem: a2 + b2 = c2 Description Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Common examples include (3, 4, 5) and (5, 12, 13).	Definition of a Triangle
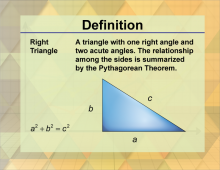
Definition--Triangle Concepts--Right Triangle	Right Triangle Topic Triangles Definition A right triangle is a triangle with one 90-degree angle. Description A right triangle is a type of triangle that has one angle measuring 90 degrees. This type of triangle is fundamental in geometry and trigonometry, as it forms the basis for the Pythagorean theorem: a2 + b2 = c2 This concept is essential in various real-world applications, such as in construction and navigation. For example, right triangles are used to create right angles and ensure accuracy in building projects. They also play a crucial role in various mathematical problems and proofs.	Definition of a Triangle
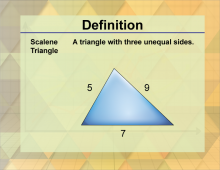
Definition--Triangle Concepts--Scalene Triangle	Scalene Triangle Topic Triangles Definition A scalene triangle is a triangle with all three sides of different lengths and all three angles of different measures. Description A scalene triangle is characterized by having all three sides of different lengths and all three angles of different measures. This type of triangle is significant in geometry as it represents a unique class of triangles with specific properties.	Definition of a Triangle
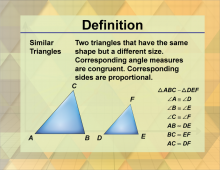
Definition--Triangle Concepts--Similar Triangles	Similar Triangles Topic Triangles Definition Similar triangles are triangles that have the same shape but not necessarily the same size, with corresponding angles equal and corresponding sides proportional. Description Similar triangles are fundamental in geometry, representing triangles that have the same shape but not necessarily the same size. This means that all corresponding angles are equal, and all corresponding sides are proportional.	Definition of a Triangle
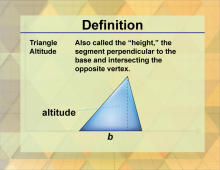
Definition--Triangle Concepts--Triangle Altitude	Triangle Altitude Topic Triangles Definition The altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side. Description The altitude of a triangle is a significant concept in geometry, representing the perpendicular distance from a vertex to the line containing the opposite side. This measurement is crucial in various geometric calculations, such as finding the area of a triangle.	Definition of a Triangle
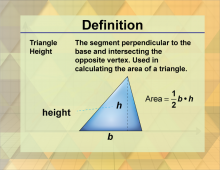
Definition--Triangle Concepts--Triangle Height	Triangle Height Topic Triangles Definition The height of a triangle is the perpendicular distance from a vertex to the line containing the opposite side, often used interchangeably with altitude. Description The height of a triangle, often used interchangeably with altitude, is a crucial concept in geometry. It represents the perpendicular distance from a vertex to the line containing the opposite side. This measurement is essential for calculating the area of a triangle, using the formula: Area= 1/2 × base × height	Definition of a Triangle
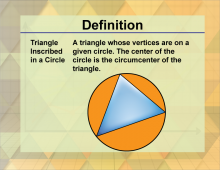
Definition--Triangle Concepts--Triangle Inscribed in a Circle	Triangle Inscribed in a Circle Topic Triangles Definition A triangle inscribed in a circle is a triangle whose vertices all lie on the circumference of the circle. Description A triangle inscribed in a circle, also known as a circumtriangle, is a triangle whose vertices all lie on the circumference of the circle. The circle is called the circumcircle, and its center is the circumcenter of the triangle.	Definition of a Triangle
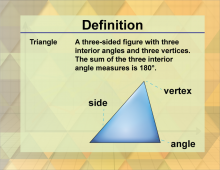
Definition--Triangle Concepts--Triangle, Definition 1	Triangle, Definition 1 Topic Triangles Definition A triangle is a polygon with three edges and three vertices. Description A triangle is one of the simplest and most fundamental shapes in geometry, characterized by having three sides and three vertices. The sum of the interior angles of a triangle is always 180 degrees, which is a key property used in various geometric proofs and constructions. In real-world applications, triangles are used extensively in engineering, architecture, and design due to their inherent stability and strength. For example, triangular structures are often used in bridges and roof trusses to distribute weight evenly and provide support.	Definition of a Triangle
Definition--Triangle Concepts--Triangle, Definition 2	Triangle, Definition 2 Topic Triangles Definition A triangle is a three-sided polygon with three vertices and three angles. Description A triangle is a three-sided polygon that is fundamental in the study of geometry. Each triangle has three vertices and three angles, and the sum of its interior angles is always 180 degrees. This property is crucial for understanding various geometric principles and solving related problems.	Definition of a Triangle
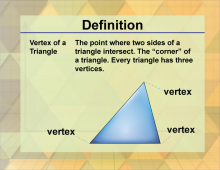
Definition--Triangle Concepts--Vertex of a Triangle	Vertex of a Triangle Topic Triangles Definition A vertex of a triangle is a point where two sides of the triangle meet. Description A vertex of a triangle is one of the three points where the sides of the triangle intersect. Each triangle has three vertices, and these points are crucial for defining the shape and properties of the triangle.	Definition of a Triangle
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Constructing an Isosceles Triangle	In this Slide Show, we show how to construct an isosceles triangle. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT.	Definition of a Triangle and Geometric Constructions with Triangles
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: The Perpendicular Bisectors of a Triangle	In this Slide Show, we show how to construct the perpendicular bisectors of the three sides of a triangle to show they intersect at a single point. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT.	Definition of a Triangle and Geometric Constructions with Triangles
INSTRUCTIONAL RESOURCE: TI-Nspire App Activity: Constructing an Isosceles Triangle	In this Slide Show, learn how to use the TI-Nspire App to construct an isosceles triangle. Note: The download is a PPT file.	Definition of a Triangle and Geometric Constructions with Triangles
Interactive Crossword Puzzle--Triangles	Interactive Crossword Puzzle--Triangles This interactive crossword puzzle tests knowledge of key terms on the topic of triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide. Related Resources To see additional resources on this topic, click on the Related Resources tab.	Definition of a Triangle
Interactive Math Game: Math Riddles--Triangles	Interactive Math Game: Math Riddles--Triangles In this Math Riddles Game, have your students review vocabulary around the topic of triangles. The Math Riddles games are useful for practicing: Math Vocabulary, Key Concepts, Critical Thinking. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide. Related Resources To see additional resources on this topic, click on the Related Resources tab.	Definition of a Triangle
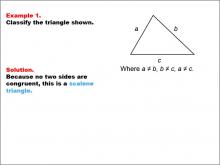
Math Example--Polygons--Triangle Classification: Example 1	Math Example--Polygons--Triangle Classification: Example 1 Topic Triangles Description This image shows a triangle with side lengths labeled as a, b, and c, where all sides are unequal. Based on the length of each side, the triangle is classified as scalene, as no two sides are congruent. Triangles are categorized based on side length (scalene, isosceles, equilateral) or angle measures (acute, obtuse, right). In this example, the scalene classification is determined by identifying that each side is a different length. The examples in this collection illustrate various classification rules based on both side and angle properties.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 10	Math Example--Polygons--Triangle Classification: Example 10 Topic Triangles Description This example presents a triangle with side lengths of 10, 10, and 8. Since two sides are congruent, the triangle is classified as isosceles. Triangle classification can be determined by side lengths or angle measures. Isosceles triangles have two equal sides or angles. Reviewing different examples assists students in identifying these types based on side or angle properties. Seeing multiple worked-out examples reinforces students’ ability to classify triangles by consistently applying classification rules.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 11	Math Example--Polygons--Triangle Classification: Example 11 Topic Triangles Description This example shows a triangle with two sides labeled as x and a third side labeled y. Because two sides are congruent, the triangle is classified as isosceles. Triangles can be classified by their side lengths or angle measures. An isosceles triangle has two equal sides or angles, as seen in this example. Reviewing a series of examples helps students understand these classifications and recognize patterns in triangles.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 12	Math Example--Polygons--Triangle Classification: Example 12 Topic Triangles Description This example shows a triangle with side lengths all equal to 9. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be classified based on side or angle properties. An equilateral triangle has all sides and angles congruent. Viewing multiple examples reinforces students’ understanding of these classifications and enhances their ability to recognize triangle properties. Seeing several worked-out examples helps students understand and apply the rules consistently for classifying triangles.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 13	Math Example--Polygons--Triangle Classification: Example 13 Topic Triangles Description This example shows a triangle with three sides labeled as x, all equal in length. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be categorized by side length or angle measures. An equilateral triangle has all congruent sides and angles. Reviewing multiple examples helps students recognize triangle classifications by observing side and angle patterns. Providing several examples reinforces students’ ability to consistently classify triangles based on the observed properties.	Definition of a Triangle
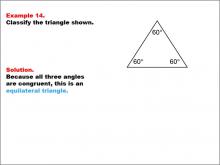
Math Example--Polygons--Triangle Classification: Example 14	Math Example--Polygons--Triangle Classification: Example 14 Topic Triangles Description This example shows a triangle with three angles, each measuring 60°. Since all angles are equal, the triangle is classified as equilateral. Triangle classification can be based on side lengths or angle measures. An equilateral triangle has all angles congruent. Reviewing examples like these helps students understand classification rules based on triangle properties. Multiple examples reinforce students' ability to identify triangle types consistently by observing angle or side characteristics.	Definition of a Triangle
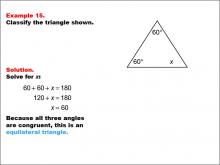
Math Example--Polygons--Triangle Classification: Example 15	Math Example--Polygons--Triangle Classification: Example 15 Topic Triangles Description This example presents a triangle with two angles labeled 60° and an unknown angle labeled x. Solving for x, we find it to be 60°, making all angles congruent and classifying the triangle as equilateral. Triangle classification can be determined by side length or angle measures. An equilateral triangle has all equal sides and angles. Observing multiple examples helps students apply these criteria consistently when classifying triangles. Seeing several worked examples helps students gain confidence in identifying triangles by recognizing congruent angles or sides.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 16	Math Example--Polygons--Triangle Classification: Example 16 Topic Triangles Description This example presents a triangle with three sides labeled as x, each equal in length. Since all three sides are congruent, the triangle is classified as equilateral. Triangles are categorized by their side lengths or angle measures. An equilateral triangle has all equal sides and angles, as seen in this example. Reviewing multiple examples reinforces students' understanding of the consistent characteristics that define each triangle type. Providing multiple worked-out examples helps students confidently apply classification rules to identify triangles by their properties.	Definition of a Triangle
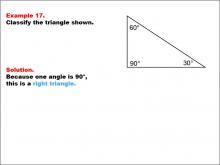
Math Example--Polygons--Triangle Classification: Example 17	Math Example--Polygons--Triangle Classification: Example 17 Topic Triangles Description This example shows a triangle with angles measuring 90°, 60°, and 30°. Since one angle is exactly 90°, the triangle is classified as a right triangle. Triangle classification often considers angle measures, with right triangles defined by having one 90° angle. Observing multiple examples allows students to consistently apply this classification rule. Reviewing various worked-out examples helps students solidify their understanding of identifying triangle types based on angle measurements.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 18	Math Example--Polygons--Triangle Classification: Example 18 Topic Triangles Description This example shows a triangle with two angles labeled 50° and 40° and an unknown angle x. Solving for x, we find it to be 90°, which classifies this as a right triangle. Triangles are classified by side lengths or angles, and a right triangle has a 90° angle. Examining examples like this helps students reinforce the criteria for identifying right triangles based on their angle properties. Seeing multiple worked-out examples enables students to apply classification rules more effectively and confidently.	Definition of a Triangle
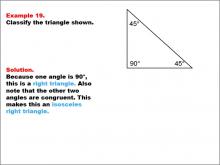
Math Example--Polygons--Triangle Classification: Example 19	Math Example--Polygons--Triangle Classification: Example 19 Topic Triangles Description This example presents a triangle with two congruent angles of 45° and one right angle of 90°. Because it has a 90° angle, the triangle is classified as a right triangle, and the two equal angles make it an isosceles right triangle. Triangle classification can involve side lengths or angles. A right triangle has a 90° angle, while isosceles triangles have two equal angles or sides. This example combines both classifications. Reviewing multiple examples helps students confidently apply the criteria to identify triangle types.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 2	Math Example--Polygons--Triangle Classification: Example 2 Topic Triangles Description This image shows a triangle with sides measuring 7, 8, and 9. The triangle is classified as scalene because each side has a different length, meaning no two sides are congruent. Triangles can be classified by examining their side lengths or angle measures. Scalene triangles, like the one shown, have no congruent sides, making them unique. This collection of examples helps students understand classification rules and visually identify different triangle types.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 20	Math Example--Polygons--Triangle Classification: Example 20 Topic Triangles Description This example shows a triangle with two known angles of 45° and an unknown angle x. Solving for x, we find it to be 90°, classifying this as a right triangle with two congruent angles, making it an isosceles right triangle. Triangle classification may be based on side lengths or angles. Right triangles have a 90° angle, while isosceles triangles have two equal sides or angles. Examples like this help students understand combined classifications.	Definition of a Triangle
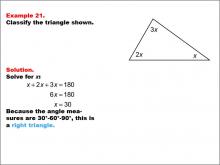
Math Example--Polygons--Triangle Classification: Example 21	Math Example--Polygons--Triangle Classification: Example 21 Topic Triangles Description This example shows a triangle with angles labeled as x, 2x, and 3x. Solving for x, we find that the angles are 30°, 60°, and 90°, classifying it as a right triangle. Triangle classification can involve angle measures or side lengths. Right triangles have one 90° angle, as seen here. Reviewing various examples supports students in consistently applying these classification rules. Observing multiple worked-out examples helps students gain confidence in identifying triangles based on the presence of specific angle measures.	Definition of a Triangle
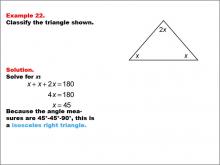
Math Example--Polygons--Triangle Classification: Example 22	Math Example--Polygons--Triangle Classification: Example 22 Topic Triangles Description This example shows a triangle with two equal angles labeled x and a third angle labeled 2x. Solving for x, we find the angles to be 45°, 45°, and 90°, classifying it as an isosceles right triangle. Triangles are classified by their angle measures or side lengths. Right triangles have a 90° angle, and isosceles triangles have two congruent angles. Reviewing examples like this one helps students understand combined classifications.	Definition of a Triangle
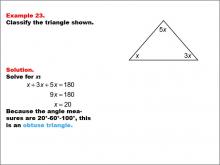
Math Example--Polygons--Triangle Classification: Example 23	Math Example--Polygons--Triangle Classification: Example 23 Topic Triangles Description This example shows a triangle with angles labeled x, 3x, and 5x. Solving for x, we find the angles to be 20°, 60°, and 100°, which classifies this triangle as obtuse because one of the angles is greater than 90°. Triangles can be classified by angle measures, with obtuse triangles defined as having one angle greater than 90°. Observing examples like this aids students in understanding how angle measures determine classifications. Providing multiple worked-out examples reinforces students' ability to consistently classify triangles based on angle properties.	Definition of a Triangle
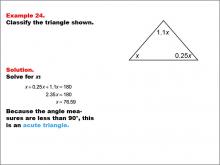
Math Example--Polygons--Triangle Classification: Example 24	Math Example--Polygons--Triangle Classification: Example 24 Topic Triangles Description This example shows a triangle with angles labeled as x, 0.25x, and 1.1x. Solving for x, we find that all angles are less than 90°, classifying the triangle as acute. Triangles are classified by their angle measures or side lengths, with acute triangles having all angles less than 90°. Reviewing examples like this helps students reinforce the criteria for classifying triangles based on angle sizes. Seeing multiple worked-out examples builds students' confidence in applying classification rules and identifying triangle types based on consistent properties.	Definition of a Triangle
Math Example--Polygons--Triangle Classification: Example 3	Math Example--Polygons--Triangle Classification: Example 3 Topic Triangles Description This example shows a triangle with side lengths of 12, 18, and x, where x is not equal to 12 or 18. The triangle is classified as scalene because all three side lengths are different. Triangles are categorized by side length or angle. Scalene triangles, with all sides unequal, demonstrate a key classification type. Multiple examples help students recognize classification patterns for triangles based on side length or angle measure. Observing various worked-out examples reinforces consistent application of classification criteria, building student confidence in identifying triangle types.	Definition of a Triangle
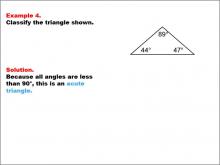
Math Example--Polygons--Triangle Classification: Example 4	Math Example--Polygons--Triangle Classification: Example 4 Topic Triangles Description This example displays a triangle with angles measuring 89°, 44°, and 47°. Since all angles are less than 90°, the triangle is classified as acute. Triangle classification can be based on side length or angle measures. Acute triangles have all angles less than 90°, as shown in this example. Reviewing multiple examples in this way helps students visually distinguish triangle types by angle. Providing varied worked-out examples solidifies students’ understanding of the criteria for each triangle type, enabling them to accurately identify triangles by their angle measures.	Definition of a Triangle
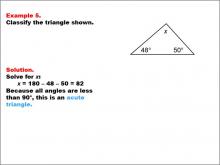
Math Example--Polygons--Triangle Classification: Example 5	Math Example--Polygons--Triangle Classification: Example 5 Topic Triangles Description This example presents a triangle with angles of 48°, 50°, and an unknown angle x. Solving for x, we find that x = 82°, meaning all angles are less than 90°, classifying it as acute. Triangles can be identified by their angles or side lengths. Acute triangles have all angles less than 90°, as seen here. Reviewing examples like this supports student understanding of angle-based classification. Seeing multiple worked examples helps students recognize patterns and confidently classify triangles based on established criteria.	Definition of a Triangle
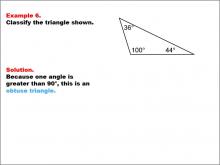
Math Example--Polygons--Triangle Classification: Example 6	Math Example--Polygons--Triangle Classification: Example 6 Topic Triangles Description This example shows a triangle with angles of 36°, 100°, and 44°. Because one of the angles is greater than 90°, this triangle is classified as obtuse. Triangles are classified by side lengths or angles. An obtuse triangle has one angle greater than 90°, as seen here. This collection of examples supports students in identifying and classifying triangles based on distinct angle measures. Seeing multiple worked-out examples reinforces students' understanding of classification rules, making it easier to recognize triangle types based on angle or side length.	Definition of a Triangle
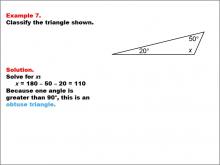
Math Example--Polygons--Triangle Classification: Example 7	Math Example--Polygons--Triangle Classification: Example 7 Topic Triangles Description This example presents a triangle with two known angles, 20° and 50°, and an unknown angle x. Solving for x, we find it to be 110°. Since one angle is greater than 90°, the triangle is classified as obtuse. Triangles can be classified by their angles, where obtuse triangles have one angle over 90°. Reviewing examples like this aids students in understanding classification based on angle measures. Seeing multiple examples reinforces the rules and helps students apply classification consistently and accurately.	Definition of a Triangle
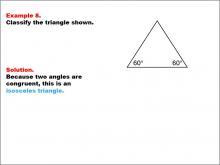
Math Example--Polygons--Triangle Classification: Example 8	Math Example--Polygons--Triangle Classification: Example 8 Topic Triangles Description This example shows a triangle with two angles, each measuring 60°. Since two angles are congruent, this triangle is classified as isosceles. Triangles can be categorized by side or angle properties. Isosceles triangles have two equal sides or two equal angles, as illustrated here. This collection of examples allows students to observe classifications and understand patterns in triangle properties. Examining multiple examples helps students confidently identify triangle types based on consistent characteristics.	Definition of a Triangle
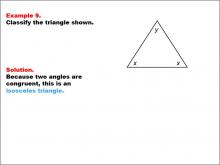
Math Example--Polygons--Triangle Classification: Example 9	Math Example--Polygons--Triangle Classification: Example 9 Topic Triangles Description This example shows a triangle with two angles labeled x and one angle labeled y. Since two angles are congruent, the triangle is classified as isosceles. Triangles can be classified by side lengths or angle measures. Isosceles triangles, with two equal sides or angles, are common. Observing various examples helps students understand these classification criteria. Providing multiple examples allows students to identify patterns in side and angle relationships, reinforcing accurate triangle classification.	Definition of a Triangle
MATH EXAMPLES--Teacher's Guide: Triangle Classification	MATH EXAMPLES--Teacher's Guide: Triangle Classification This set of tutorials provides 24 examples that show how to identify different types of triangles and how to solve for x using the properties of triangles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Definition of a Triangle

Illustrative Math Alignment: Grade 7 Unit 7

Angles, Triangles, and Prisms

Lesson 10: Drawing Triangles (Part 2)

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Topic

Definition

Description

Related Resources

Related Resources

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic