Illustrative Math Alignment: Grade 7 Unit 9

Overview

Overview

Overview

Overview

Overview

The Fractions definitions collection from Media4Math is an invaluable resource for students and educators aiming to master or teach the fundamental concepts of fractions. This comprehensive set includes 20 essential terms, each presented as a downloadable PNG image card, making it easy to integrate into classroom presentations or study materials.

Overview

Overview

Overview

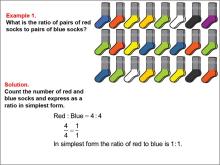
Overview

This collection of math examples on Ratios and Rates from Media4Math offers a comprehensive resource for students to develop essential mathematical skills. Comprising 32 carefully curated examples, the collection increases in complexity, allowing learners to progress from basic concepts to more challenging applications. 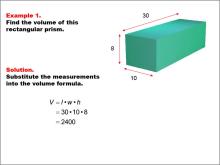Each example utilizes visual models, which serve to simplify the understanding of ratios and rates, making abstract ideas more tangible.

Overview

Overview

This collection of math examples on the topic of Volume provides students with an in-depth exploration of volume concepts through a variety of visual models. Covering a range of skills and increasing in complexity, this collection helps students master foundational and advanced topics in volume. From calculating the volume of basic geometric shapes to applying volume formulas to complex objects, these examples build confidence and enhance comprehension by breaking down challenging concepts visually.

Overview

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Data Analysis

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

In this video students learn the basics of antiprisms, in the context of New York’s Freedom Tower, which has an antiprism design. They learn the properties of antiprisms, with the focus on those with a square base.

In this video students learn the basics of antiprisms, in the context of New York’s Freedom Tower, which has an antiprism design. They learn the properties of antiprisms, with the focus on those with a square base.

In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms.

In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms.

In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms.

In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms.

In this video students study a real-world application of triangular prisms: The Flat Iron Building in New York City. This building is an ideal example of a real-world prism and also provides a tie-in to right triangle geometry. This video describes the geometry of the Flat Iron Building, as well as its architecture. It includes animations that demonstrate the key features of triangular prisms.

In this video students study a real-world application of triangular prisms: The Flat Iron Building in New York City. This building is an ideal example of a real-world prism and also provides a tie-in to right triangle geometry. This video describes the geometry of the Flat Iron Building, as well as its architecture. It includes animations that demonstrate the key features of triangular prisms.