
Illustrative Math Alignment: Grade 8 Unit 2
Dilations, Similarity, and Introducing Slope
Lesson 5: More Dilations
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
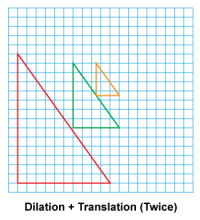
Math Clip Art--Geometry Concepts--Similarity with Transformations--08 | Math Clip Art--Similarity with Transformations--08TopicGeometry Concepts DescriptionThis image shows a triangle undergoing a combination of dilation and translation performed twice. The dilation changes the size of the triangle while maintaining its shape, and the translations move it to new positions. This complex transformation demonstrates how multiple transformations can be applied repeatedly. The resulting triangles are similar to the original but differ in size and position. |
Proportions |
|
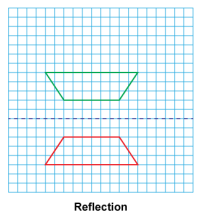
Math Clip Art--Geometry Concepts--Similarity with Transformations--09 | Math Clip Art--Similarity with Transformations--09TopicGeometry Concepts DescriptionThis image depicts a trapezoid reflected across a horizontal line. Reflection creates a mirror image of the original figure across a line of reflection. This transformation demonstrates how a figure can be flipped over a line to create its mirror image. The resulting trapezoid is congruent to the original but inverted vertically. Teacher's Script: "Observe how the trapezoid is reflected across the horizontal line. What properties of the trapezoid remain unchanged? How does the orientation of the trapezoid change after reflection? Can you identify the line of reflection?" |
Proportions |
|
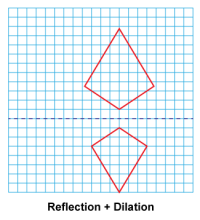
Math Clip Art--Geometry Concepts--Similarity with Transformations--10 | Math Clip Art--Similarity with Transformations--10TopicGeometry Concepts DescriptionThis image shows a kite reflected across a horizontal line, followed by a dilation. Reflection creates a mirror image of the original figure across a line of reflection. Dilation changes the size of the original figure but keeps it proportional. This transformation demonstrates how a figure can be flipped over a line to create its mirror image. The resulting kite is similar to the original but inverted vertically. |
Proportions |
|
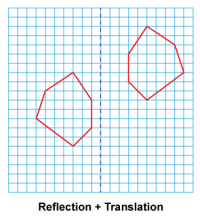
Math Clip Art--Geometry Concepts--Similarity with Transformations--11 | Math Clip Art--Similarity with Transformations--11TopicGeometry Concepts DescriptionThis image illustrates an irregular hexagon reflected across a vertical line. Reflection creates a mirror image of the original figure across a line of reflection. This transformation demonstrates how a complex figure can be flipped over a vertical line to create its mirror image. The resulting hexagon is congruent to the original but reversed horizontally. |
Proportions |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art: Comparing Right Triangles | Math Clip Art: Comparing Right Triangles Use these clip art images and the background grid to test if the right triangles are similar. |
Right Triangles |
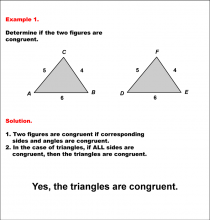
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
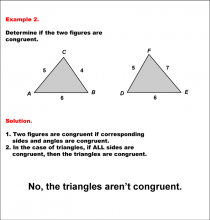
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
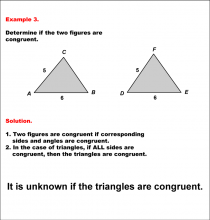
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
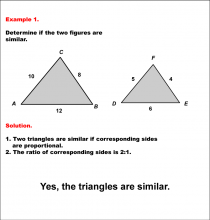
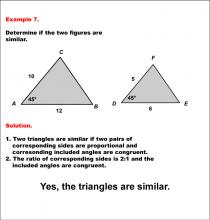
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 4, and 6. Triangles are similar if corresponding sides are proportional. Here, the ratio of corresponding sides is 2:1 (10:5, 8:4, 12:6). Thus, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has angle 40°, and the other triangle has a 60° angle. For similarity, all corresponding angles must be congruent. The angles in each triangle do not match, so the triangles aren't similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
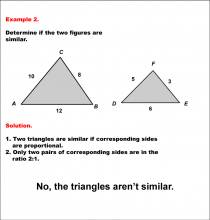
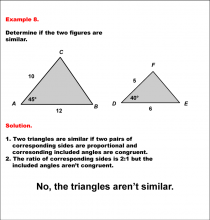
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 3, and 6. Triangles are similar if all corresponding sides are proportional. Only two pairs of sides here have a 2:1 ratio, so the triangles are not similar. Therefore, the answer is No, the triangles arenÕt similar. |
Definition of a Triangle |
|
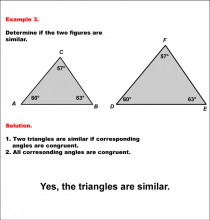
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Both triangles have angles 60°, 57°, and 63°. Triangles are similar if corresponding angles are equal. Since all corresponding angles match, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has angles 75°, 42°, and an unknown angle, and triangle DEF has angles 75° and 63° and an unknown angles. Triangles are similar if all corresponding angles are congruent. Solving for the unknown angles confirms angle congruency, so the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two right triangles, ABC and DEF, are similar. Triangle ABC has angles 90° and 40°, and triangle DEF has angles 90° and 50°. Triangles are similar if all corresponding angles are congruent. Solving reveals congruent corresponding angles. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has a right angle and an angle of 40°, and triangle DEF has a right angle and 45°. Not all corresponding angles are congruent, so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |
|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 45° angle. Triangles are similar if two pairs of sides are proportional, and the included angle is congruent. The side ratio is 2:1, and both included angles are 45°. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |
|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 40° angle. Triangles are similar if two pairs of sides are proportional, and the included angles are congruent. Here, the included angles differ (45° vs. 40°), so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
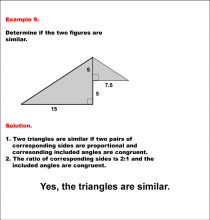
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has sides 10 and 15 and an included right angle, while the other triangle has sides 5 and 7.5 and an included right angle. Triangles are similar if two pairs of corresponding sides are proportional, and corresponding included angles are congruent. The side ratio is 2:1, and the included right angles are congruent. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |
|
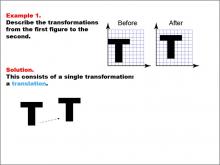
Math Example--Geometric Transformation--Transformations: Example 1 | Math Example--Geometric Transformation--Transformations: Example 1TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two "T" shapes are shown on a grid, labeled "Before" and "After". The "Before" shape on the left is translated to become the "After" shape on the right, illustrating how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
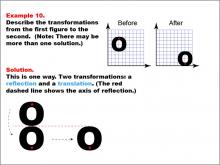
Math Example--Geometric Transformation--Transformations: Example 10 | Math Example--Geometric Transformation--Transformations: Example 10TopicTransformations DescriptionThis example showcases a combination of reflection and translation in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". A red dashed line indicates the axis of reflection. The transformation involves first reflecting the shape across this axis and then translating it to a new position. This demonstrates how multiple transformations can be applied in sequence to create more complex movements. |
Definition of Transformations |
|
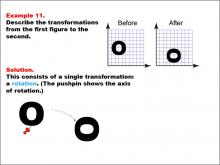
Math Example--Geometric Transformation--Transformations: Example 11 | Math Example--Geometric Transformation--Transformations: Example 11TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. Two circular "O" shapes are shown on a grid, one labeled "Before" and the other "After". The shape undergoes a rotation around a point indicated by a pushpin, which serves as the axis of rotation. This illustrates how an object can change its orientation without altering its size or position relative to the rotation point. |
Definition of Transformations |
|
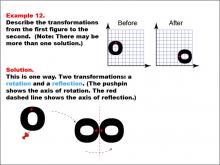
Math Example--Geometric Transformation--Transformations: Example 12 | Math Example--Geometric Transformation--Transformations: Example 12TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". The transformation involves two steps: first, a rotation around a point indicated by a pushpin, which serves as the axis of rotation, followed by a reflection across a red dashed line representing the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
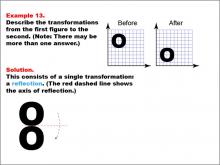
Math Example--Geometric Transformation--Transformations: Example 13 | Math Example--Geometric Transformation--Transformations: Example 13TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. Two grids are shown with the letter "O" before and after a transformation. The "Before" grid has the "O" on the left side, while the "After" grid has it on the right side. A red dashed line indicates the axis of reflection in the middle of the two "O"s. Below, there is a diagram showing the reflection transformation along this axis, illustrating how the shape is flipped across the line while maintaining its size and shape. |
Definition of Transformations |
|
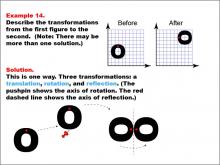
Math Example--Geometric Transformation--Transformations: Example 14 | Math Example--Geometric Transformation--Transformations: Example 14TopicTransformations DescriptionThis example illustrates a complex combination of transformations: translation, rotation, and reflection. Two grids are shown with an "O" shape before and after transformations. The "Before" grid has an "O" with a red dot at its center, while the "After" grid shows the same "O" but rotated and reflected. Below, a step-by-step diagram illustrates three sequential transformations: first, a translation moves the shape, then a rotation turns it around a pushpin (indicating the axis of rotation), and finally, a reflection flips it across a red dashed line. |
Definition of Transformations |
|
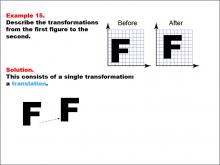
Math Example--Geometric Transformation--Transformations: Example 15 | Math Example--Geometric Transformation--Transformations: Example 15TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two grids are displayed with the letter "F" before and after a transformation. The "Before" grid shows an "F" on the left side, and the "After" grid shows it on the right side. Below, there is an arrow indicating that only a translation occurred between the two positions of the letter, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
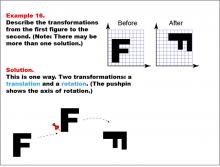
Math Example--Geometric Transformation--Transformations: Example 16 | Math Example--Geometric Transformation--Transformations: Example 16TopicTransformations DescriptionThis example demonstrates a combination of translation and rotation in geometric transformations. Two grids are shown with the letter "F" before and after transformations. The "Before" grid has an upright "F", while the "After" grid shows it rotated 90 degrees clockwise. Below, there is a diagram illustrating two steps: first, a translation moves the shape, then a rotation turns it around a pushpin axis. |
Definition of Transformations |

|
Math Example--Geometric Transformation--Transformations: Example 17 | Math Example--Geometric Transformation--Transformations: Example 17TopicTransformations DescriptionThis example illustrates a combination of reflection and translation in geometric transformations. The image shows a large letter "F" on a grid transforming into a letter "L". The transformation involves two steps: first, a reflection across an axis represented by a red dashed line, and then a translation to a new position. |
Definition of Transformations |
|
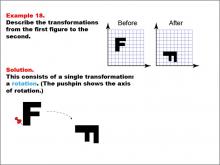
Math Example--Geometric Transformation--Transformations: Example 18 | Math Example--Geometric Transformation--Transformations: Example 18TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows the letter "F" on a grid being rotated to form the same letter in a different orientation. A pushpin indicates the axis of rotation, and an arrow shows the direction of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
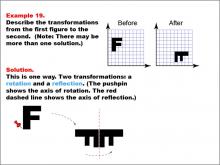
Math Example--Geometric Transformation--Transformations: Example 19 | Math Example--Geometric Transformation--Transformations: Example 19TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows the letter "F" being transformed into an upside-down version of itself. This transformation involves two steps: first, a rotation around an axis indicated by a pushpin, followed by a reflection across a line represented by a red dashed line. |
Definition of Transformations |
|
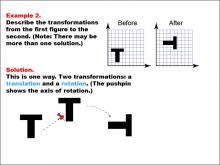
Math Example--Geometric Transformation--Transformations: Example 2 | Math Example--Geometric Transformation--Transformations: Example 2TopicTransformations DescriptionThis example illustrates a combination of transformations: translation and rotation. Two "T" shapes are shown on a grid, labeled "Before" and "After". The shape undergoes a translation (movement) and a rotation, with a pushpin indicating the axis of rotation. This demonstrates how multiple transformations can be applied sequentially to a shape. |
Definition of Transformations |
|
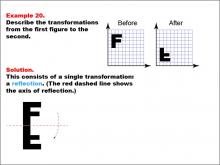
Math Example--Geometric Transformation--Transformations: Example 20 | Math Example--Geometric Transformation--Transformations: Example 20TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows the letter "F" being reflected to form the letter "L". A red dashed line indicates the axis of reflection, illustrating how the letter changes its orientation through this single transformation. This showcases how an object can be flipped over a line while changing its shape and orientation. |
Definition of Transformations |
|
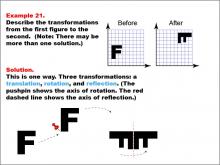
Math Example--Geometric Transformation--Transformations: Example 21 | Math Example--Geometric Transformation--Transformations: Example 21TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows an uppercase letter "F" on a grid labeled "Before" and a transformed version of the letter "F" upside down on another grid labeled "After." Below, there are illustrations showing the three steps of the transformation process. |
Definition of Transformations |
|
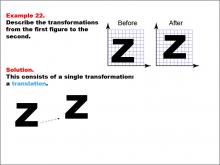
Math Example--Geometric Transformation--Transformations: Example 22 | Math Example--Geometric Transformation--Transformations: Example 22TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a horizontally shifted version of the same letter on another grid labeled "After." Below, there is an illustration showing just a translation, indicating that the letter "Z" is moved horizontally without any rotation or reflection. |
Definition of Transformations |
|
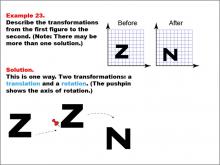
Math Example--Geometric Transformation--Transformations: Example 23 | Math Example--Geometric Transformation--Transformations: Example 23TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and an uppercase letter "N" on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first a translation (moving the figure) followed by a rotation (turning the figure). A pushpin indicates the axis of rotation. |
Definition of Transformations |
|
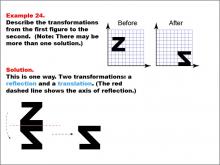
Math Example--Geometric Transformation--Transformations: Example 24 | Math Example--Geometric Transformation--Transformations: Example 24TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a rotated and translated version of the same letter in another position on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first, a reflection (flipping the figure across an axis shown by the red dashed line) and then a translation (moving the figure). |
Definition of Transformations |
|
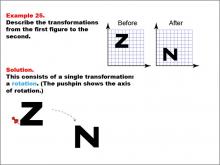
Math Example--Geometric Transformation--Transformations: Example 25 | Math Example--Geometric Transformation--Transformations: Example 25TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a transformation of the letter "Z" from an upright position to a rotated position resembling "N". The grid background helps visualize the transformation, and a pushpin icon indicates the axis of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |