Illustrative Math-Media4Math Alignment

Illustrative Math Alignment: Grade 8 Unit 2

Dilations, Similarity, and Introducing Slope

Lesson 6: Similarity

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image	Title	Body	Curriculum Topic
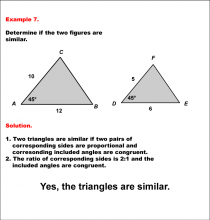
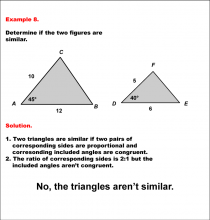
	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 40° angle. Triangles are similar if two pairs of sides are proportional, and the included angles are congruent. Here, the included angles differ (45° vs. 40°), so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar.	Definition of a Triangle
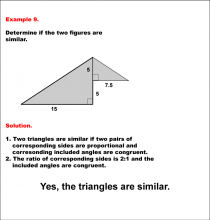
	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9 Topic Geometric Shapes Description Determine if two right triangles are similar. The triangle on the left has sides 10 and 15 and an included right angle, while the other triangle has sides 5 and 7.5 and an included right angle. Triangles are similar if two pairs of corresponding sides are proportional, and corresponding included angles are congruent. The side ratio is 2:1, and the included right angles are congruent. Therefore, the answer is Yes, the triangles are similar.	Definition of a Triangle
	Video Transcript: Geometry Applications: Triangles	Video Transcript: Geometry Applications: Triangles This is the transcript for the video of same title. Video contents: In this program we explore the properties of triangle. We do this in the context of two real-world applications. In the first, we explore the triangular trusses in the Eiffel Tower and in the process learn about key properties of triangles. In the second application, we look at right-triangle-shaped sails on sail boat and why these are the ideal shape for efficient sailing.	Applications of Triangles
	Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction	Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction This is the transcript for the video of same title. Video contents: The Bank of China building in Hong Kong is a dramatic example of triangular support. The notion of triangular trusses is introduced, along with the key concepts developed in the rest of the program. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript Library To see the complete collection of video transcriptsy, click on this link.	Applications of Triangles
	Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles	Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles This is the transcript for the video of same title. Video contents: The Eiffel Tower includes quite a number of exposed triangular trusses. The properties of triangles are used to explore and explain the frequent use of triangular trusses in many building. In particular, isosceles and equilateral triangular trusses are explored. In addition triangle postulates and similarity are explored and analyzed.	Applications of Triangles
	Video Tutorial: Slope and Similar Triangles	Video Tutorial: Slope and Similar Triangles In this video explore the relationship between slope and similar triangles.	Slope
	VIDEO: Geometry Applications: Triangles, 2	VIDEO: Geometry Applications: Triangles, 2 Topic Triangles	Applications of Triangles