
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 5: Introduction to Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 10 | Math Example--Linear Function Concepts--Linear Function Machines--Example 10TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x + 1. This involves creating a table of values for x and f(x) using f(x) = 3x + 1. The output for each x is calculated by tripling x and then adding 1. The results are f(x) = -5, -2, 1, 4, and 7 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 10 | Math Example--Linear Function Concepts--Linear Function Machines--Example 10TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x + 1. This involves creating a table of values for x and f(x) using f(x) = 3x + 1. The output for each x is calculated by tripling x and then adding 1. The results are f(x) = -5, -2, 1, 4, and 7 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 11 | Math Example--Linear Function Concepts--Linear Function Machines--Example 11TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 4 * x + 1. This involves a table created for x and f(x) values. By substituting each x value into f(x) = 4 * x + 1, the outputs are calculated as follows: -2 gives -7, -1 gives -3, 0 gives 1, 1 gives 5, and 2 gives 9. The common difference between successive outputs is +4, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 11 | Math Example--Linear Function Concepts--Linear Function Machines--Example 11TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 4 * x + 1. This involves a table created for x and f(x) values. By substituting each x value into f(x) = 4 * x + 1, the outputs are calculated as follows: -2 gives -7, -1 gives -3, 0 gives 1, 1 gives 5, and 2 gives 9. The common difference between successive outputs is +4, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 11 | Math Example--Linear Function Concepts--Linear Function Machines--Example 11TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 4 * x + 1. This involves a table created for x and f(x) values. By substituting each x value into f(x) = 4 * x + 1, the outputs are calculated as follows: -2 gives -7, -1 gives -3, 0 gives 1, 1 gives 5, and 2 gives 9. The common difference between successive outputs is +4, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 12 | Math Example--Linear Function Concepts--Linear Function Machines--Example 12TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 5 * x + 1. This involves a table created for x and f(x) values. substituting each x into f(x) = 5 * x + 1, the outputs are calculated: -2 gives -9, -1 gives -4, 0 gives 1, 1 gives 6, and 2 gives 11. the common difference between outputs is +5, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 12 | Math Example--Linear Function Concepts--Linear Function Machines--Example 12TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 5 * x + 1. This involves a table created for x and f(x) values. substituting each x into f(x) = 5 * x + 1, the outputs are calculated: -2 gives -9, -1 gives -4, 0 gives 1, 1 gives 6, and 2 gives 11. the common difference between outputs is +5, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 12 | Math Example--Linear Function Concepts--Linear Function Machines--Example 12TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 5 * x + 1. This involves a table created for x and f(x) values. substituting each x into f(x) = 5 * x + 1, the outputs are calculated: -2 gives -9, -1 gives -4, 0 gives 1, 1 gives 6, and 2 gives 11. the common difference between outputs is +5, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
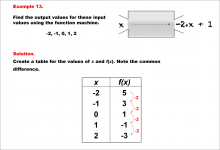
Math Example--Linear Function Concepts--Linear Function Machines--Example 13 | Math Example--Linear Function Concepts--Linear Function Machines--Example 13TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -2 * x + 1. This involves a table created for x and f(x) values. Substituting each x into f(x) = -2 * x + 1, the outputs are: -2 gives 5, -1 gives 3, 0 gives 1, 1 gives -1, and 2 gives -3. The common difference is -2, indicating a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 13 | Math Example--Linear Function Concepts--Linear Function Machines--Example 13TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -2 * x + 1. This involves a table created for x and f(x) values. Substituting each x into f(x) = -2 * x + 1, the outputs are: -2 gives 5, -1 gives 3, 0 gives 1, 1 gives -1, and 2 gives -3. The common difference is -2, indicating a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 13 | Math Example--Linear Function Concepts--Linear Function Machines--Example 13TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -2 * x + 1. This involves a table created for x and f(x) values. Substituting each x into f(x) = -2 * x + 1, the outputs are: -2 gives 5, -1 gives 3, 0 gives 1, 1 gives -1, and 2 gives -3. The common difference is -2, indicating a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
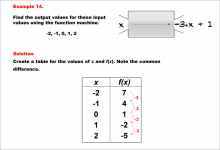
Math Example--Linear Function Concepts--Linear Function Machines--Example 14 | Math Example--Linear Function Concepts--Linear Function Machines--Example 14TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -3 * x + 1. This involves a table created for x and f(x) values. Each x substituted into f(x) = -3 * x + 1 yields: -2 gives 7, -1 gives 4, 0 gives 1, 1 gives -2, and 2 gives -5. The common difference is -3, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 14 | Math Example--Linear Function Concepts--Linear Function Machines--Example 14TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -3 * x + 1. This involves a table created for x and f(x) values. Each x substituted into f(x) = -3 * x + 1 yields: -2 gives 7, -1 gives 4, 0 gives 1, 1 gives -2, and 2 gives -5. The common difference is -3, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 14 | Math Example--Linear Function Concepts--Linear Function Machines--Example 14TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -3 * x + 1. This involves a table created for x and f(x) values. Each x substituted into f(x) = -3 * x + 1 yields: -2 gives 7, -1 gives 4, 0 gives 1, 1 gives -2, and 2 gives -5. The common difference is -3, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |
|
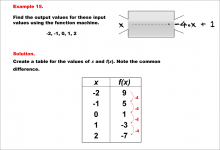
Math Example--Linear Function Concepts--Linear Function Machines--Example 15 | Math Example--Linear Function Concepts--Linear Function Machines--Example 15TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -4 * x + 1. This involves a table is created for x and f(x) values. Calculating for each x: -2 gives 9, -1 gives 5, 0 gives 1, 1 gives -3, and 2 gives -7. The common difference is -4, indicating linearity. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 15 | Math Example--Linear Function Concepts--Linear Function Machines--Example 15TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -4 * x + 1. This involves a table is created for x and f(x) values. Calculating for each x: -2 gives 9, -1 gives 5, 0 gives 1, 1 gives -3, and 2 gives -7. The common difference is -4, indicating linearity. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 15 | Math Example--Linear Function Concepts--Linear Function Machines--Example 15TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -4 * x + 1. This involves a table is created for x and f(x) values. Calculating for each x: -2 gives 9, -1 gives 5, 0 gives 1, 1 gives -3, and 2 gives -7. The common difference is -4, indicating linearity. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |
|
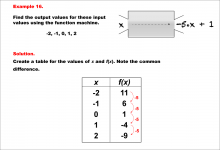
Math Example--Linear Function Concepts--Linear Function Machines--Example 16 | Math Example--Linear Function Concepts--Linear Function Machines--Example 16TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -5 * x + 1. This involves a table created for x and f(x) values. Substituting into f(x) = -5 * x + 1, the outputs are: -2 gives 11, -1 gives 6, 0 gives 1, 1 gives -4, and 2 gives -9. The common difference is -5, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 16 | Math Example--Linear Function Concepts--Linear Function Machines--Example 16TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -5 * x + 1. This involves a table created for x and f(x) values. Substituting into f(x) = -5 * x + 1, the outputs are: -2 gives 11, -1 gives 6, 0 gives 1, 1 gives -4, and 2 gives -9. The common difference is -5, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 16 | Math Example--Linear Function Concepts--Linear Function Machines--Example 16TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -5 * x + 1. This involves a table created for x and f(x) values. Substituting into f(x) = -5 * x + 1, the outputs are: -2 gives 11, -1 gives 6, 0 gives 1, 1 gives -4, and 2 gives -9. The common difference is -5, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 17 | Math Example--Linear Function Concepts--Linear Function Machines--Example 17TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 2. This involves a table created for x and f(x) values, where f(x) = 2 for all x values, resulting in outputs of 2, 2, 2, 2, and 2. The common difference is 0, indicating a constant function: y = 2. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 17 | Math Example--Linear Function Concepts--Linear Function Machines--Example 17TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 2. This involves a table created for x and f(x) values, where f(x) = 2 for all x values, resulting in outputs of 2, 2, 2, 2, and 2. The common difference is 0, indicating a constant function: y = 2. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 17 | Math Example--Linear Function Concepts--Linear Function Machines--Example 17TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 2. This involves a table created for x and f(x) values, where f(x) = 2 for all x values, resulting in outputs of 2, 2, 2, 2, and 2. The common difference is 0, indicating a constant function: y = 2. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 18 | Math Example--Linear Function Concepts--Linear Function Machines--Example 18TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 0. This involves a table created for x and f(x) values, where f(x) = 0 for all x values, giving outputs of 0, 0, 0, 0, and 0. The common difference is 0, indicating a constant function: y = 0. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 18 | Math Example--Linear Function Concepts--Linear Function Machines--Example 18TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 0. This involves a table created for x and f(x) values, where f(x) = 0 for all x values, giving outputs of 0, 0, 0, 0, and 0. The common difference is 0, indicating a constant function: y = 0. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 18 | Math Example--Linear Function Concepts--Linear Function Machines--Example 18TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 0. This involves a table created for x and f(x) values, where f(x) = 0 for all x values, giving outputs of 0, 0, 0, 0, and 0. The common difference is 0, indicating a constant function: y = 0. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 19 | Math Example--Linear Function Concepts--Linear Function Machines--Example 19TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = -1. This involves a table created for x and f(x) values, where f(x) = -1 for all x values, resulting in outputs of -1, -1, -1, -1, and -1. The common difference is 0, indicating a constant function: y = -1. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 19 | Math Example--Linear Function Concepts--Linear Function Machines--Example 19TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = -1. This involves a table created for x and f(x) values, where f(x) = -1 for all x values, resulting in outputs of -1, -1, -1, -1, and -1. The common difference is 0, indicating a constant function: y = -1. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 19 | Math Example--Linear Function Concepts--Linear Function Machines--Example 19TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = -1. This involves a table created for x and f(x) values, where f(x) = -1 for all x values, resulting in outputs of -1, -1, -1, -1, and -1. The common difference is 0, indicating a constant function: y = -1. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 2 | Math Example--Linear Function Concepts--Linear Function Machines--Example 2TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x. This involves creating a table of values for x and f(x) using f(x) = 3x. The output for each x is calculated by multiplying x by 3. the results are f(x) = -6, -3, 0, 3, and 6 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 2 | Math Example--Linear Function Concepts--Linear Function Machines--Example 2TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x. This involves creating a table of values for x and f(x) using f(x) = 3x. The output for each x is calculated by multiplying x by 3. the results are f(x) = -6, -3, 0, 3, and 6 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 2 | Math Example--Linear Function Concepts--Linear Function Machines--Example 2TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x. This involves creating a table of values for x and f(x) using f(x) = 3x. The output for each x is calculated by multiplying x by 3. the results are f(x) = -6, -3, 0, 3, and 6 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 3 | Math Example--Linear Function Concepts--Linear Function Machines--Example 3TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 4x. This involves creating a table of values for x and f(x) using f(x) = 4x. The output for each x is calculated by multiplying x by 4. The results are f(x) = -8, -4, 0, 4, and 8 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 3 | Math Example--Linear Function Concepts--Linear Function Machines--Example 3TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 4x. This involves creating a table of values for x and f(x) using f(x) = 4x. The output for each x is calculated by multiplying x by 4. The results are f(x) = -8, -4, 0, 4, and 8 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 3 | Math Example--Linear Function Concepts--Linear Function Machines--Example 3TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 4x. This involves creating a table of values for x and f(x) using f(x) = 4x. The output for each x is calculated by multiplying x by 4. The results are f(x) = -8, -4, 0, 4, and 8 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 4 | Math Example--Linear Function Concepts--Linear Function Machines--Example 4TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 5x. This involves creating a table of values for x and f(x) using f(x) = 5x. The output for each x is calculated by multiplying x by 5. The results are f(x) = -10, -5, 0, 5, and 10 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 4 | Math Example--Linear Function Concepts--Linear Function Machines--Example 4TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 5x. This involves creating a table of values for x and f(x) using f(x) = 5x. The output for each x is calculated by multiplying x by 5. The results are f(x) = -10, -5, 0, 5, and 10 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 4 | Math Example--Linear Function Concepts--Linear Function Machines--Example 4TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 5x. This involves creating a table of values for x and f(x) using f(x) = 5x. The output for each x is calculated by multiplying x by 5. The results are f(x) = -10, -5, 0, 5, and 10 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 5 | Math Example--Linear Function Concepts--Linear Function Machines--Example 5TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -2x. This involves creating a table of values for x and f(x) using f(x) = -2x. The output for each x is calculated by multiplying x by -2. The results are f(x) = 4, 2, 0, -2, and -4 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 5 | Math Example--Linear Function Concepts--Linear Function Machines--Example 5TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -2x. This involves creating a table of values for x and f(x) using f(x) = -2x. The output for each x is calculated by multiplying x by -2. The results are f(x) = 4, 2, 0, -2, and -4 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 5 | Math Example--Linear Function Concepts--Linear Function Machines--Example 5TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -2x. This involves creating a table of values for x and f(x) using f(x) = -2x. The output for each x is calculated by multiplying x by -2. The results are f(x) = 4, 2, 0, -2, and -4 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 6 | Math Example--Linear Function Concepts--Linear Function Machines--Example 6TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -3x. This involves creating a table of values for x and f(x) using f(x) = -3x. The output for each x is calculated by multiplying x by -3. The results are f(x) = 6, 3, 0, -3, and -6 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 6 | Math Example--Linear Function Concepts--Linear Function Machines--Example 6TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -3x. This involves creating a table of values for x and f(x) using f(x) = -3x. The output for each x is calculated by multiplying x by -3. The results are f(x) = 6, 3, 0, -3, and -6 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 6 | Math Example--Linear Function Concepts--Linear Function Machines--Example 6TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -3x. This involves creating a table of values for x and f(x) using f(x) = -3x. The output for each x is calculated by multiplying x by -3. The results are f(x) = 6, 3, 0, -3, and -6 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 7 | Math Example--Linear Function Concepts--Linear Function Machines--Example 7TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -4x. This involves creating a table of values for x and f(x) using f(x) = -4x. The output for each x is calculated by multiplying x by -4. The results are f(x) = 8, 4, 0, -4, and -8 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 7 | Math Example--Linear Function Concepts--Linear Function Machines--Example 7TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -4x. This involves creating a table of values for x and f(x) using f(x) = -4x. The output for each x is calculated by multiplying x by -4. The results are f(x) = 8, 4, 0, -4, and -8 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 7 | Math Example--Linear Function Concepts--Linear Function Machines--Example 7TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -4x. This involves creating a table of values for x and f(x) using f(x) = -4x. The output for each x is calculated by multiplying x by -4. The results are f(x) = 8, 4, 0, -4, and -8 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 8 | Math Example--Linear Function Concepts--Linear Function Machines--Example 8TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -5x. This involves creating a table of values for x and f(x) using f(x) = -5x. The output for each x is calculated by multiplying x by -5. The results are f(x) = 10, 5, 0, -5, and -10 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 8 | Math Example--Linear Function Concepts--Linear Function Machines--Example 8TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -5x. This involves creating a table of values for x and f(x) using f(x) = -5x. The output for each x is calculated by multiplying x by -5. The results are f(x) = 10, 5, 0, -5, and -10 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 8 | Math Example--Linear Function Concepts--Linear Function Machines--Example 8TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -5x. This involves creating a table of values for x and f(x) using f(x) = -5x. The output for each x is calculated by multiplying x by -5. The results are f(x) = 10, 5, 0, -5, and -10 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |