
Illustrative Math Alignment: Grade 8 Unit 7
Exponents and Scientific Notation
Lesson 11: Representing Small Numbers on the Number Line
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Worksheet Collection: Scientific Notation |
OverviewThis collection aggregates all the math worksheets around the topic of Scientific Notation. There are a total of 40 worksheets. Each worksheet includes an answer key. This collection of resources is made up of downloadable PDF files that you can easily incorporate into your instruction.To download the full set of these resources, click on this link.
|
Numerical Expressions |

|
Math Quiz Collection: The Laws of Exponents |
OverviewThis collection aggregates all the math quizzes on this topic: The Laws of Exponents. There are a total of 3 resources. This collection of quizzes is made up of downloadable PDFs. To download the full set of these resources, click on this link.
|
Laws of Exponents |

|
Math Examples Collection: Integer and Rational Exponents | OverviewThis collection from Media4Math on Integer and Rational Exponents offers a comprehensive set of examples on the topic of exponents. These examples gradually increase in complexity, covering a range of skills including integer and rational exponents, simplifying expressions, and applying exponent rules. Each example is supported by visual models to help simplify concepts, making it easier for students to understand the various properties of exponents. |
Numerical Expressions |

|
Math Definitions Collection: Exponential and Logarithmic Vocabulary | OverviewThis collection aggregates all the definition image cards around the topic of Exponential and Logarithmic vocabulary. There are a total of 11 terms. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.
|
Applications of Exponential and Logarithmic Functions |

|
Math in the News Collection: Applications of Numerical and Algebraic Expressions |
OverviewThis is a collection of Math in the News stories that focus on the topic of Numerical and Algebraic Expressions.
|
Numerical Expressions and Variable Expressions |

|
Math Examples Collection: The Laws of Exponents | OverviewThis comprehensive collection of 24 Math Examples focuses on the Laws of Exponents, providing educators with a rich resource to enhance their lesson plans. This set of downloadable images covers a wide range of skills related to exponent manipulation. |
Laws of Exponents |

|
Closed Captioned Video: Algebra Nspirations: Exponents | Closed Captioned Video: Algebra Nspirations: Exponents and Exponential Functions
Almost everyone has an intuitive understanding that exponential growth means rapid growth. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video builds on students’ intuitive notions, explores exponential notation, and analyzes properties of exponential function graphs, with the help of TI-Nspire features such as sliders and graph transformations. Using exponential functions to model finance applications and a Newton’s law of cooling problem further help students build a solid foundation for these fundamental algebraic concepts. Concepts explored: functions, exponents, exponential functions. |
Applications of Exponential and Logarithmic Functions, Exponential and Logarithmic Functions and Equations and Graphs of Exponential and Logarithmic Functions |

|
Closed Captioned Video: Algebra Nspirations: Exponents, 3 | Closed Captioned Video: Algebra Nspirations: Exponents and Exponential Functions, Segment 3
In this Investigation we look at exponential growth and decay models. This video is Segment 3 of a 4 segment series related to Exponents and Exponential Functions. Segments 3 and 4 are grouped together. In this episode of Algebra Applications, students explore earthquakes using exponential models. In particular, students analyze the earthquake that struck the Sichuan Province in China in 2008, months before the Beijing Olympics. This dramatic, real-world example allows students to apply their understanding of exponential functions and their inverses, along with data analysis and periodic function analysis. —PRESS PREVIEW TO SEE THE VIDEO—This is part of a collection of videos from the Algebra Applications video series on the topic of Exponential Functions. |
Applications of Exponential and Logarithmic Functions, Exponential and Logarithmic Functions and Equations and Graphs of Exponential and Logarithmic Functions |

|
Closed Captioned Video: Algebra Nspirations: Exponents, 1 | Closed Captioned Video: Algebra Nspirations: Exponents and Exponential Functions, Segment 1
In this Investigation we explore the properties of exponents and exponential graphs. This video is Segment 1 of a 4 segment series related to Exponents and Exponential Functions. Segments 1 and 2 are grouped together. In this episode of Algebra Applications, students explore earthquakes using exponential models. In particular, students analyze the earthquake that struck the Sichuan Province in China in 2008, months before the Beijing Olympics. This dramatic, real-world example allows students to apply their understanding of exponential functions and their inverses, along with data analysis and periodic function analysis. —PRESS PREVIEW TO SEE THE VIDEO—This is part of a collection of videos from the Algebra Applications video series on the topic of Exponential Functions. |
Applications of Exponential and Logarithmic Functions, Exponential and Logarithmic Functions and Equations and Graphs of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Compound Interest 1 | Definition--Exponential Concepts--Compound Interest 1
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Compound Interest 2 | Definition--Exponential Concepts--Compound Interest 2
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Exponent | Definition--Exponential Concepts--Exponent
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |
|
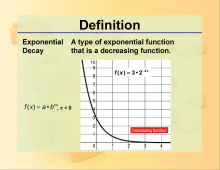
Definition--Exponential Concepts--Exponential Decay | Definition--Exponential Concepts--Exponential Decay
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Exponential Equation | Definition--Exponential Concepts--Exponential Equation
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Exponential Function | Definition--Exponential Concepts--Exponential Function
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |
|
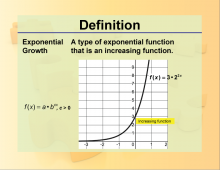
Definition--Exponential Concepts--Exponential Growth | Definition--Exponential Concepts--Exponential Growth
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Exponential Models | Definition--Exponential Concepts--Exponential Models
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |
|
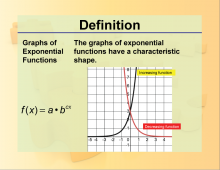
Definition--Exponential Concepts--Graphs of Exponential Functions | Definition--Exponential Concepts--Graphs of Exponential Functions
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |
|
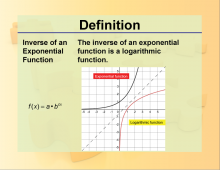
Definition--Exponential Concepts--Inverse of an Exponential Function | Definition--Exponential Concepts--Inverse of an Exponential Function
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Laws of Exponents | Definition--Exponential Concepts--Laws of Exponents
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Exponential Concepts--Laws of Exponents | Definition--Exponential Concepts--Laws of Exponents
This is a collection of definitions related to exponential concepts. This includes exponential functions, equations, and properties of exponents. |
Applications of Exponential and Logarithmic Functions |

|
Definition--Scientific Notation | Definition--Scientific Notation
This is part of a collection of definitions on various math topics. |
Numerical Expressions and Variable Expressions |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous? | INSTRUCTIONAL RESOURCE: Algebra Application: Why Are Wildfires So Dangerous?
In this Algebra Application, students learn about wildfires and the measurement of air quality. The math topics covered include: Scientific notation, Rates, Density, Data Analysis. The specific focus of this investigation is the health hazards from wildfire smoke. This includes a discussion of air density, measurement in microns, and measurement of air quality. Links to various web sites, including the EPA's site, provide relevant background information and data. The culminating activity is a case study of the wildfires in the Lake Tahoe area. Students analyze historical data and make a recommendation on the air quality. This is a great back-to-school activity for middle school or high school students. A relevant real-world application allows them to review math concepts. |
Laws of Exponents and Applications of Ratios, Proportions, and Percents |

|
INSTRUCTIONAL RESOURCE: Math Examples 24 | INSTRUCTIONAL RESOURCE: Math Examples--Laws of Exponents
The complete set of 24 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Laws of Exponents |

|
INSTRUCTIONAL RESOURCE: Tutorial: The Laws of Exponents | INSTRUCTIONAL RESOURCE: Tutorial: The Laws of Exponents
In this tutorial we walk students through the Laws of Exponents. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 1TopicExponents DescriptionShows Example 1 with the expression 32. The solution explains how to simplify by multiplying 3 by itself according to the exponent. Example 1: Simplify 32. Multiply 3 by itself two times: 3•3 = 9. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 10TopicExponents DescriptionShows Example 10 with the expression (-3)3•54. The solution uses order of operations to evaluate each term before multiplying. Example 10: Simplify (-3)3•54. Evaluate each exponential term separately, then multiply: -27•625= -16,875. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 11TopicExponents DescriptionExample 11 shows how to simplify (1/2)2. The image illustrates multiplying 1/2 by itself due to the exponent of 2. Example 11: Simplify (1/2)2. Multiply one-half two times. Solution: (1/2) * (1/2) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 12TopicExponents DescriptionExample 12 shows how to simplify (1/3)4. The image illustrates multiplying 1/3 four times due to the exponent of 4. Example 12: Simplify (1/3)4. Multiply one-third four times. Solution: (1/3) * (1/3) * (1/3) * (1/3) = 1/81. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 13TopicExponents DescriptionExample 13 shows how to simplify (-1/3)3. The image illustrates multiplying -1/3 three times due to the exponent of 3. Example 13: Simplify (-1/3)3. Multiply negative one-third three times. Solution: (-1/3) * (-1/3) * (-1/3) = -1/27. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 14TopicExponents DescriptionExample 14 shows how to simplify 2-1. The image illustrates rewriting 2-1 as the reciprocal of 2 raised to the first power. Example 14: Simplify 2-1. Negative exponents are written as reciprocals. Solution: 2-1 = 1/2. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 15TopicExponents DescriptionExample 15 shows how to simplify 2-2. The image illustrates rewriting 2-2 as the reciprocal of 2 raised to the second power. Example 15: Simplify 2-2. Negative exponents are written as reciprocals. Solution: 2-2 = 1/(22) = 1/4. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 2TopicExponents DescriptionShows Example 2 with the expression 43. The solution explains the simplification by multiplying 4 three times. Example 2: Simplify 43. Multiply 4 by itself three times: 4•4•4 = 64. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 3TopicExponents DescriptionShows Example 3 with the expression 54. The solution details multiplying 5 four times. Example 3: Simplify 54. Multiply 5 by itself four times: 5•5•5•5 = 625. In general, the topic of exponents involves understanding how repeated multiplication can be expressed more compactly. The examples provided in this collection allow students to see the step-by-step breakdown of how to simplify various exponential expressions, which can include positive and negative bases, fractional bases, and negative exponents. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 4TopicExponents DescriptionShows Example 4 with the expression 106. The solution simplifies by multiplying 10 six times. Example 4: Simplify 106. Multiply 10 by itself six times: 10•10•10•10•10•10 = 1,000,000. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 5 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 5TopicExponents DescriptionShows Example 5 with the expression (-1)2. The solution explains the result by multiplying -1 by itself. Example 5: Simplify (-1)2. Multiply -1 by itself two times: (-1)•(-1) = 1. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 6 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 6TopicExponents DescriptionShows Example 6 with the expression (-5)3. The solution demonstrates multiplying -5 three times. Example 6: Simplify (_5)3. Multiply -5 by itself three times: (-5)•(-5)•(-5) = -125. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 7 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 7TopicExponents DescriptionShows Example 7 with the expression (-6)4. The solution explains multiplying -6 by itself four times. Example 7: Simplify (-6)4. Multiply -6 by itself four times: (-6)•(-6)•(-6)•(-6) = 1296. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 8 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 8TopicExponents DescriptionShows Example 8 with the expression 23•32. The solution demonstrates using order of operations to simplify each term separately, then multiply. Example 8: Simplify 23•32. Evaluate each exponential term separately, then multiply: 8•9 = 72. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Integer and Rational Exponents--Example 9 | Math Example--Exponential Concepts--Integer and Rational Exponents--Example 9TopicExponents DescriptionShows Example 9 with the expression (-1)2•43. The solution explains simplifying each term individually before multiplying. Example 9: Simplify (-1)2•43. Evaluate each exponential term separately, then multiply: 1•64 = 64. |
Numerical Expressions |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 1 | Math Example--Exponential Concepts--Laws of Exponents: Example 1TopicExponents DescriptionThis example demonstrates the simplification of an expression using the laws of exponents. The problem involves simplifying x2 * x3, which results in x5 by applying the law of exponents for multiplication. This step-by-step solution helps students understand how to combine like terms with exponents. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 10 | Math Example--Exponential Concepts--Laws of Exponents: Example 10TopicExponents DescriptionThis example focuses on simplifying an expression with both positive and negative exponents. The problem involves simplifying x3 * x(-5) * x(-3), which results in x(-5) or 1/x5. This demonstrates how positive and negative exponents interact when multiplying terms with the same base, and how the result can be expressed as a fraction. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 11 | Math Example--Exponential Concepts--Laws of Exponents: Example 11TopicExponents DescriptionThis example demonstrates the simplification of an expression with both positive and negative exponents, including a zero exponent. The problem involves simplifying x(-10) * x10 * x(-2), which results in x(-2) or 1/x2. This showcases how positive and negative exponents interact when multiplying terms with the same base, and how zero exponents affect the result. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 12 | Math Example--Exponential Concepts--Laws of Exponents: Example 12TopicExponents DescriptionThis example focuses on simplifying an expression with multiple negative exponents. The problem involves simplifying x(-1) * x(-5) * x(-3), which results in x(-9) or 1/x9. This demonstrates how negative exponents interact when multiplying terms with the same base, and how the result can be expressed as a fraction with a positive exponent in the denominator. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 13 | Math Example--Exponential Concepts--Laws of Exponents: Example 13TopicExponents DescriptionThis example demonstrates the simplification of an expression involving division with exponents. The problem involves simplifying x3 / x2, which results in x. This showcases how exponents behave when dividing terms with the same base, illustrating the subtraction of exponents in division. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 14 | Math Example--Exponential Concepts--Laws of Exponents: Example 14TopicExponents DescriptionThis example demonstrates the simplification of an expression involving division with negative exponents. The problem involves simplifying x(-5) / x6, which results in x(-11) or 1/x11. This showcases how negative and positive exponents interact when dividing terms with the same base, and how the result can be expressed as a fraction. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 15 | Math Example--Exponential Concepts--Laws of Exponents: Example 15TopicExponents DescriptionThis example illustrates the simplification of an expression involving division with both positive and negative exponents. The problem involves simplifying x8 / x(-4), which results in x12. This demonstrates how positive and negative exponents interact when dividing terms with the same base, and how the result can yield a larger positive exponent. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 16 | Math Example--Exponential Concepts--Laws of Exponents: Example 16TopicExponents DescriptionThis example focuses on simplifying an expression with negative exponents in both the numerator and denominator. The problem involves simplifying x(-7) / x(-5), which results in x(-2) or 1/x2. This demonstrates how negative exponents interact when dividing terms with the same base, and how the result can be expressed as a fraction. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 17 | Math Example--Exponential Concepts--Laws of Exponents: Example 17TopicExponents DescriptionThis example demonstrates the simplification of an expression involving multiplication and division with exponents. The problem involves simplifying (x2 * x3) / x4, which results in x. This showcases how exponents behave when multiplying and dividing terms with the same base, illustrating the addition and subtraction of exponents in a single expression. |
Laws of Exponents |

|
Math Example--Exponential Concepts--Laws of Exponents: Example 18 | Math Example--Exponential Concepts--Laws of Exponents: Example 18TopicExponents DescriptionThis example focuses on simplifying an expression involving multiplication and division with both positive and negative exponents. The problem involves simplifying (x-3 * x5) / x6, which results in x-4 or 1/x4. This demonstrates how positive and negative exponents interact when multiplying and dividing terms with the same base, and how the result can be expressed as a fraction. |
Laws of Exponents |