
Illustrative Math Alignment: Grade 8 Unit 8
Pythagorean Theorem and Irrational Numbers
Lesson 6: Finding Side Lengths of Triangles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
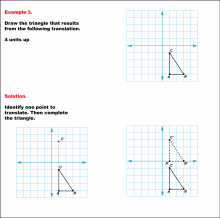
Math Example--Geometric Transformation--Translating Triangles--Example 3 | Math Example--Geometric Transformation--Translating Triangles--Example 3TopicTransformations DescriptionA triangle on a grid is translated 4 units up. The figure displays both the original and translated triangles ABC and A'B'C'.. Example 3: "Draw the triangle that results from the following translation: 4 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
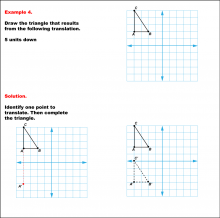
Math Example--Geometric Transformation--Translating Triangles--Example 4 | Math Example--Geometric Transformation--Translating Triangles--Example 4TopicTransformations DescriptionA triangle on a grid is translated 5 units down. It shows the original triangle and its new position after translation, labeled A'B'C'. Example 4: "Draw the triangle that results from the following translation: 5 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
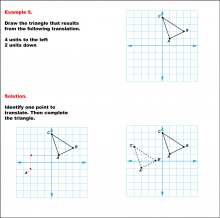
Math Example--Geometric Transformation--Translating Triangles--Example 5 | Math Example--Geometric Transformation--Translating Triangles--Example 5TopicTransformations DescriptionA triangle is translated 4 units to the left and 2 units down. Both the original and the new triangles, ABC and A'B'C', are illustrated. Example 5: "Draw the triangle that results from the following translation: 4 units to the left, 2 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
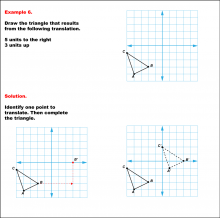
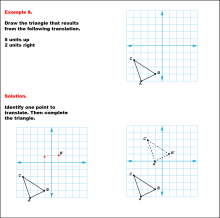
Math Example--Geometric Transformation--Translating Triangles--Example 6 | Math Example--Geometric Transformation--Translating Triangles--Example 6TopicTransformations DescriptionThe triangle is translated 5 units to the right and 3 units up. The image includes both original and translated triangles, labeled ABC and A'B'C'. Example 6: "Draw the triangle that results from the following translation: 5 units to the right, 3 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
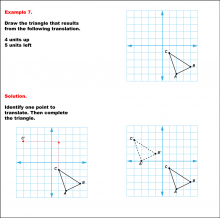
Math Example--Geometric Transformation--Translating Triangles--Example 7 | Math Example--Geometric Transformation--Translating Triangles--Example 7TopicTransformations DescriptionA triangle is translated 4 units up and 5 units left, showing the original ABC and translated A'B'C' triangles. Example 7: "Draw the triangle that results from the following translation: 4 units up, 5 units left." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
Math Example--Geometric Transformation--Translating Triangles--Example 8 | Math Example--Geometric Transformation--Translating Triangles--Example 8TopicTransformations Description
The triangle is translated 5 units up and 2 units right. The image shows both the original and translated positions of the triangle. Example 8: "Draw the triangle that results from the following translation: 5 units up, 2 units rogjt." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
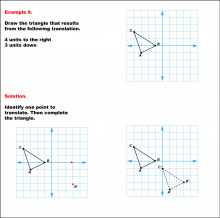
Math Example--Geometric Transformation--Translating Triangles--Example 9 | Math Example--Geometric Transformation--Translating Triangles--Example 9TopicTransformations DescriptionA triangle is translated 4 units to the right and 3 units down. The image shows both the original and the new triangle positions. Example 9: "Draw the triangle that results from the following translation: 4 units to the right, 3 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |

|
Math Example--Polygons--Quadrilateral Classification: Example 1 | Math Example--Polygons--Quadrilateral Classification: Example 1TopicGeometry DescriptionThis example presents a quadrilateral with labeled sides: AB = 5, BC = 4, CD = 3, and DA = 6. The task is to classify the quadrilateral based on these measurements. Since none of the sides are congruent and no specific relationships among the sides can be determined, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 10 | Math Example--Polygons--Quadrilateral Classification: Example 10TopicGeometry DescriptionThis example showcases a quadrilateral with right angles labeled with variable x at two corners, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This means all angles are 90 degrees. Since opposite sides are parallel and congruent, we can classify this shape as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 11 | Math Example--Polygons--Quadrilateral Classification: Example 11TopicGeometry DescriptionThis example presents a square with all sides congruent and right angles, labeled as A, B, C, and D. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and all sides are congruent, this shape is confirmed to be a square. |
Definition of a Quadrilateral |
|
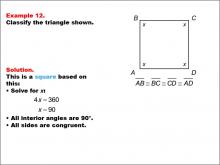
Math Example--Polygons--Quadrilateral Classification: Example 12 | Math Example--Polygons--Quadrilateral Classification: Example 12TopicGeometry DescriptionThis example features a quadrilateral with all sides labeled x and marked congruent, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 4x = 360, which gives us x = 90. This means all angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 13 | Math Example--Polygons--Quadrilateral Classification: Example 13TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. To classify this shape, we solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This confirms that all interior angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 14 | Math Example--Polygons--Quadrilateral Classification: Example 14TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. Each side is labeled with a length of 1. Based on these characteristics, we can classify this shape as a square. All sides are congruent, which means opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 15 | Math Example--Polygons--Quadrilateral Classification: Example 15TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. Based on these characteristics, we can classify this shape as a square. Because all sides are congruent, opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 16 | Math Example--Polygons--Quadrilateral Classification: Example 16TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with two sides labeled with lengths of 5 and x, and angles marked as right angles. The diagram shows perpendicular lines and parallel lines. Based on these characteristics, we can classify this shape as a square. Because angle ABC and angle BAD are supplementary, BC and AD are parallel. Since AB and CD are congruent, angle BAD and angle ADC are supplementary. Therefore, all interior angles are 90 degrees, and all sides are congruent. |
Definition of a Quadrilateral |
|
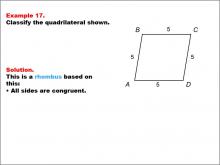
Math Example--Polygons--Quadrilateral Classification: Example 17 | Math Example--Polygons--Quadrilateral Classification: Example 17TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with all sides marked as 5 units, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The key property that defines a rhombus is that all sides are congruent, which is clearly demonstrated in this example. |
Definition of a Quadrilateral |
|
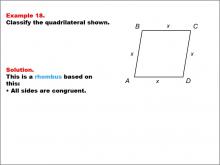
Math Example--Polygons--Quadrilateral Classification: Example 18 | Math Example--Polygons--Quadrilateral Classification: Example 18TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with all sides marked as x, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The defining property of a rhombus is that all sides are congruent, which is clearly demonstrated in this example by using the variable x for all side lengths. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 19 | Math Example--Polygons--Quadrilateral Classification: Example 19TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides AB and CD marked as x, and BC and AD marked as 5. Opposite sides are noted to be parallel. Based on these characteristics, we can classify this shape as a rhombus. The key properties that define this as a rhombus are: opposite sides are parallel, and opposite sides are congruent. Since x = 5, all sides are congruent, which is a defining property of a rhombus. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 2 | Math Example--Polygons--Quadrilateral Classification: Example 2TopicGeometry DescriptionThis example showcases a quadrilateral with sides labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the sides are given, and no sides are stated to be congruent, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |
|
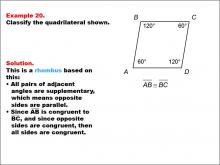
Math Example--Polygons--Quadrilateral Classification: Example 20 | Math Example--Polygons--Quadrilateral Classification: Example 20TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles B and D marked as 120 degrees, and angles A and C as 60 degrees. Sides AB and BC are marked as congruent. Based on these characteristics, we can classify this shape as a rhombus. All pairs of adjacent angles are supplementary (120° + 60° = 180°), which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |
|
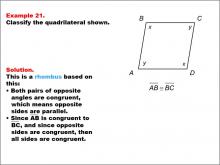
Math Example--Polygons--Quadrilateral Classification: Example 21 | Math Example--Polygons--Quadrilateral Classification: Example 21TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 22 | Math Example--Polygons--Quadrilateral Classification: Example 22TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles marked as 70° and sides marked as x. Opposite angles are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus. |
Definition of a Quadrilateral |
|
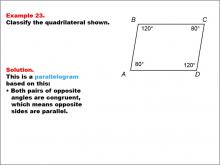
Math Example--Polygons--Quadrilateral Classification: Example 23 | Math Example--Polygons--Quadrilateral Classification: Example 23TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles marked as 120° and 80°. Opposite angles are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
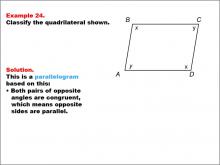
Math Example--Polygons--Quadrilateral Classification: Example 24 | Math Example--Polygons--Quadrilateral Classification: Example 24TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite sides are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
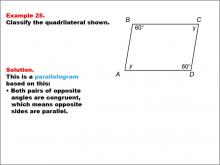
Math Example--Polygons--Quadrilateral Classification: Example 25 | Math Example--Polygons--Quadrilateral Classification: Example 25TopicGeometry DescriptionThis example showcases a quadrilateral labeled ABCD with angles at B and D marked as 60 degrees. Sides AD and BC are labeled y. The shape is identified as a parallelogram. This classification is based on the fact that both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
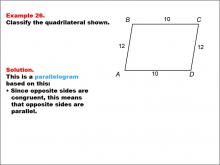
Math Example--Polygons--Quadrilateral Classification: Example 26 | Math Example--Polygons--Quadrilateral Classification: Example 26TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides AB and CD measuring 10, and sides BC and AD measuring 12. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |
|
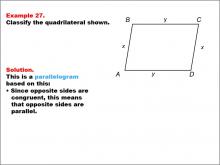
Math Example--Polygons--Quadrilateral Classification: Example 27 | Math Example--Polygons--Quadrilateral Classification: Example 27TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with sides AB and CD labeled y, and sides AD and BC labeled x. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 28 | Math Example--Polygons--Quadrilateral Classification: Example 28TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with sides BC and AD parallel, and AB and CD parallel. Side BC is marked as 5, and side AD is marked as x. Based on these characteristics, we can classify this shape as a parallelogram. Opposite sides are parallel (BC // AD, AB // CD), which is the defining property of a parallelogram. However, adjacent sides are not necessarily congruent, as BC is 5 and AD is x. |
Definition of a Quadrilateral |
|
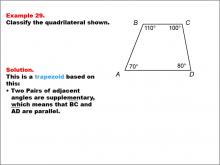
Math Example--Polygons--Quadrilateral Classification: Example 29 | Math Example--Polygons--Quadrilateral Classification: Example 29TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles marked as 110°, 100°, 70°, and 80°. Two pairs of adjacent angles are supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
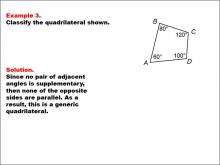
Math Example--Polygons--Quadrilateral Classification: Example 3 | Math Example--Polygons--Quadrilateral Classification: Example 3TopicGeometry DescriptionThis example presents a quadrilateral with labeled angles: A = 60°, B = 80°, C = 120°, and D = 100°. The task is to classify the quadrilateral based on these angle measurements. Since no pair of adjacent angles is supplementary (adds up to 180°), none of the opposite sides are parallel. As a result, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |
|
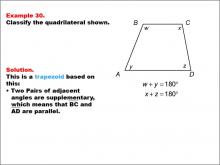
Math Example--Polygons--Quadrilateral Classification: Example 30 | Math Example--Polygons--Quadrilateral Classification: Example 30TopicGeometry DescriptionThis example features a quadrilateral labeled ABCD with angles marked as w, x, y, and z. It states that w + y = 180° and x + z = 180°. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
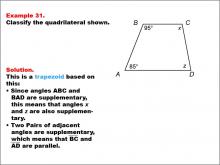
Math Example--Polygons--Quadrilateral Classification: Example 31 | Math Example--Polygons--Quadrilateral Classification: Example 31TopicGeometry DescriptionThis example presents a quadrilateral labeled ABCD with angles ABC = 95° and BAD = 85°. It states that angles x and z are also supplementary due to two pairs of adjacent angles being supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel. |
Definition of a Quadrilateral |
|
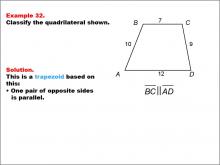
Math Example--Polygons--Quadrilateral Classification: Example 32 | Math Example--Polygons--Quadrilateral Classification: Example 32TopicGeometry DescriptionThis example showcases a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 10, BC = 7, CD = 9, and AD = 12. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |
|
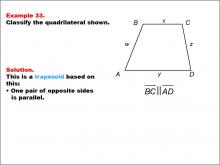
Math Example--Polygons--Quadrilateral Classification: Example 33 | Math Example--Polygons--Quadrilateral Classification: Example 33TopicGeometry DescriptionThis example presents a trapezoid with vertices labeled A, B, C, D. The sides are labeled as w, x, y, and z. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |
|
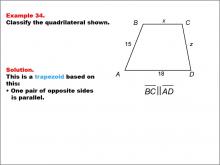
Math Example--Polygons--Quadrilateral Classification: Example 34 | Math Example--Polygons--Quadrilateral Classification: Example 34TopicGeometry DescriptionThis example features a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 15, BC = x, CD = z, and AD = 18. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 4 | Math Example--Polygons--Quadrilateral Classification: Example 4TopicGeometry DescriptionThis example features a quadrilateral with angles labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the angles are given, and no angles are stated to be congruent or supplementary, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 5 | Math Example--Polygons--Quadrilateral Classification: Example 5TopicGeometry DescriptionThis example presents a quadrilateral with no right angles or congruent sides, labeled with angles and side lengths. The task is to classify the quadrilateral based on these characteristics. Since no adjacent angles are supplementary and no sides are parallel, this shape is classified as a generic quadrilateral. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 6 | Math Example--Polygons--Quadrilateral Classification: Example 6TopicGeometry DescriptionThis example showcases a rectangle with opposite sides labeled as 3 and 1, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As the shape has opposite sides that are congruent and all interior angles are 90 degrees, it is identified as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 7 | Math Example--Polygons--Quadrilateral Classification: Example 7TopicGeometry DescriptionThis example presents a rectangle with opposite sides labeled x and y, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. Due to the congruent opposite sides and all interior angles being 90 degrees, this shape is identified as a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 8 | Math Example--Polygons--Quadrilateral Classification: Example 8TopicGeometry DescriptionThis example features a rectangle with sides labeled 7 and 5, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and opposite sides are parallel and congruent, this shape is confirmed to be a rectangle. |
Definition of a Quadrilateral |

|
Math Example--Polygons--Quadrilateral Classification: Example 9 | Math Example--Polygons--Quadrilateral Classification: Example 9TopicGeometry DescriptionThis example presents a quadrilateral with all right angles, labeled as A, B, C, and D. The opposite sides are parallel and congruent. Based on these characteristics, the shape is classified as a rectangle. All interior angles are 90 degrees, and the opposite sides are both parallel and congruent, which are defining properties of a rectangle. |
Definition of a Quadrilateral |
|
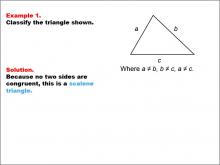
Math Example--Polygons--Triangle Classification: Example 1 | Math Example--Polygons--Triangle Classification: Example 1TopicTriangles DescriptionThis image shows a triangle with side lengths labeled as a, b, and c, where all sides are unequal. Based on the length of each side, the triangle is classified as scalene, as no two sides are congruent. Triangles are categorized based on side length (scalene, isosceles, equilateral) or angle measures (acute, obtuse, right). In this example, the scalene classification is determined by identifying that each side is a different length. The examples in this collection illustrate various classification rules based on both side and angle properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 10 | Math Example--Polygons--Triangle Classification: Example 10TopicTriangles DescriptionThis example presents a triangle with side lengths of 10, 10, and 8. Since two sides are congruent, the triangle is classified as isosceles. Triangle classification can be determined by side lengths or angle measures. Isosceles triangles have two equal sides or angles. Reviewing different examples assists students in identifying these types based on side or angle properties. Seeing multiple worked-out examples reinforces students’ ability to classify triangles by consistently applying classification rules. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 11 | Math Example--Polygons--Triangle Classification: Example 11TopicTriangles DescriptionThis example shows a triangle with two sides labeled as x and a third side labeled y. Because two sides are congruent, the triangle is classified as isosceles. Triangles can be classified by their side lengths or angle measures. An isosceles triangle has two equal sides or angles, as seen in this example. Reviewing a series of examples helps students understand these classifications and recognize patterns in triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 12 | Math Example--Polygons--Triangle Classification: Example 12TopicTriangles DescriptionThis example shows a triangle with side lengths all equal to 9. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be classified based on side or angle properties. An equilateral triangle has all sides and angles congruent. Viewing multiple examples reinforces students’ understanding of these classifications and enhances their ability to recognize triangle properties. Seeing several worked-out examples helps students understand and apply the rules consistently for classifying triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 13 | Math Example--Polygons--Triangle Classification: Example 13TopicTriangles DescriptionThis example shows a triangle with three sides labeled as x, all equal in length. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be categorized by side length or angle measures. An equilateral triangle has all congruent sides and angles. Reviewing multiple examples helps students recognize triangle classifications by observing side and angle patterns. Providing several examples reinforces students’ ability to consistently classify triangles based on the observed properties. |
Definition of a Triangle |
|
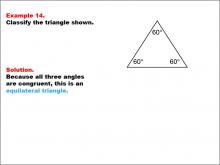
Math Example--Polygons--Triangle Classification: Example 14 | Math Example--Polygons--Triangle Classification: Example 14TopicTriangles DescriptionThis example shows a triangle with three angles, each measuring 60°. Since all angles are equal, the triangle is classified as equilateral. Triangle classification can be based on side lengths or angle measures. An equilateral triangle has all angles congruent. Reviewing examples like these helps students understand classification rules based on triangle properties. Multiple examples reinforce students' ability to identify triangle types consistently by observing angle or side characteristics. |
Definition of a Triangle |
|
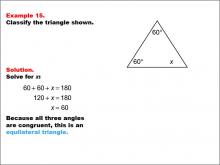
Math Example--Polygons--Triangle Classification: Example 15 | Math Example--Polygons--Triangle Classification: Example 15TopicTriangles DescriptionThis example presents a triangle with two angles labeled 60° and an unknown angle labeled x. Solving for x, we find it to be 60°, making all angles congruent and classifying the triangle as equilateral. Triangle classification can be determined by side length or angle measures. An equilateral triangle has all equal sides and angles. Observing multiple examples helps students apply these criteria consistently when classifying triangles. Seeing several worked examples helps students gain confidence in identifying triangles by recognizing congruent angles or sides. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 16 | Math Example--Polygons--Triangle Classification: Example 16TopicTriangles DescriptionThis example presents a triangle with three sides labeled as x, each equal in length. Since all three sides are congruent, the triangle is classified as equilateral. Triangles are categorized by their side lengths or angle measures. An equilateral triangle has all equal sides and angles, as seen in this example. Reviewing multiple examples reinforces students' understanding of the consistent characteristics that define each triangle type. Providing multiple worked-out examples helps students confidently apply classification rules to identify triangles by their properties. |
Definition of a Triangle |
|
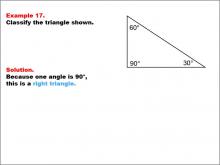
Math Example--Polygons--Triangle Classification: Example 17 | Math Example--Polygons--Triangle Classification: Example 17TopicTriangles DescriptionThis example shows a triangle with angles measuring 90°, 60°, and 30°. Since one angle is exactly 90°, the triangle is classified as a right triangle. Triangle classification often considers angle measures, with right triangles defined by having one 90° angle. Observing multiple examples allows students to consistently apply this classification rule. Reviewing various worked-out examples helps students solidify their understanding of identifying triangle types based on angle measurements. |
Definition of a Triangle |