
Illustrative Math Alignment: Grade 8 Unit 9
Putting It All Together
Lesson 3: Tessellating Polygons
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Clip Art--Geometry Concepts--Kite Shape 16 | Math Clip Art--Kite Shape 16TopicGeometry Concepts DescriptionThis image illustrates a triangular-shaped kite. Geometrically, a kite is a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. Teacher's Script: "Observe this kite. How is this a kite in the everyday sense? Is this a kite in the geometric sense?" |
Definition of a Polygon and Definition of a Triangle |
|
Math Clip Art--Geometry Concepts--Kite Shape 2 | Math Clip Art--Kite Shape 2TopicGeometry Concepts DescriptionThis image depicts another variation of a kite shape, in this case a circular shape. Geometrically, a kite is characterized by two pairs of adjacent equal-length sides and diagonals that intersect at right angles. This geometric configuration is symmetrical and unique. Kite shapes are used to explore geometric properties such as symmetry, area, and perimeter. They are applicable in various fields, including mathematics, design, and architecture. Teacher's Script: "Look at this kite. How is it a kite in the everyday sense? Is it a kite in a geometric sense?" |
Definition of a Circle, Definition of a Polygon and Definition of a Triangle |
|
Math Clip Art--Geometry Concepts--Kite Shape 3 | Math Clip Art--Kite Shape 3TopicGeometry Concepts DescriptionThis image illustrates a circular kite shape. Geometrically, a kite is a a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. Teacher's Script: "Observe this kite. How is a kite in the everyday sense of the word? Is it a kite in the geometric sense?" |
Definition of a Circle, Definition of a Polygon and Definition of a Triangle |
|
Math Clip Art--Geometry Concepts--Kite Shape 4 | Math Clip Art--Kite Shape 4TopicGeometry Concepts DescriptionThis image features a hexagonal kite shape. Geometrically, a kite is a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. Teacher's Script: "Examine this kite. How is it a kite in the everyday sense? Is it a kite in a geometric sense?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 5 | Math Clip Art--Kite Shape 5TopicGeometry Concepts DescriptionThis image depicts a hexagonal kite shape. Geometrically, a kite is characterized by two pairs of adjacent equal-length sides and diagonals that intersect at right angles. This geometric configuration is symmetrical and unique. Kite shapes are used to explore geometric properties such as symmetry, area, and perimeter. They are applicable in various fields, including mathematics, design, and architecture. Teacher's Script: "Look at this kite. How is this a kite in the everydays sense of the word? Is it a kite in the geometric sense?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 6 | Math Clip Art--Kite Shape 6TopicGeometry Concepts DescriptionThis image illustrates a hexagonal kite shape. Geometrically, a kite is a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. Teacher's Script: "Observe this kite. How is it a kite in the everyday sense? Is it a kite in the geometric sense?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 7 | Math Clip Art--Kite Shape 7TopicGeometry Concepts DescriptionThis image features a kite shape, a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. |
Definition of a Polygon and Definition of a Triangle |
|
Math Clip Art--Geometry Concepts--Kite Shape 8 | Math Clip Art--Kite Shape 8TopicGeometry Concepts DescriptionThis image depicts a kite shape, characterized by two pairs of adjacent equal-length sides and diagonals that intersect at right angles. This geometric configuration is symmetrical and unique. Kite shapes are used to explore geometric properties such as symmetry, area, and perimeter. They are applicable in various fields, including mathematics, design, and architecture. Teacher's Script: "Look at this kite shape. How do its symmetrical properties and intersecting diagonals help us understand its geometry? What are some mathematical concepts you can explore using kite shapes?" |
Definition of a Polygon and Definition of a Triangle |

|
Math Clip Art--Geometry Concepts--Kite Shape 9 | Math Clip Art--Kite Shape 9TopicGeometry Concepts DescriptionThis image illustrates a kite shape, a quadrilateral with two pairs of adjacent equal-length sides and diagonals that intersect at right angles. The symmetry and unique properties of kite shapes make them interesting geometric figures. Kite shapes are used to explore properties such as symmetry, area, and perimeter. They are applicable in various mathematical contexts, including geometry and design. |
Definition of a Polygon and Definition of a Triangle |
|
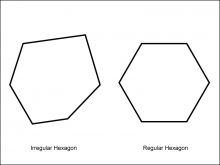
Math Clip Art--Geometry Concepts--Polygons--Hexagon | Math Clip Art--Polygons--HexagonTopicGeometry Concepts DescriptionThis image illustrates two hexagons: one regular and one irregular. A hexagon is a six-sided polygon. In a regular hexagon, all sides and angles are equal, with each interior angle measuring 120 degrees. This symmetry gives it a balanced and uniform appearance. An irregular hexagon, by contrast, has sides and angles that are not all equal. This lack of uniformity means that the hexagon can take on a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
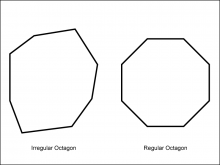
Math Clip Art--Geometry Concepts--Polygons--Octagon | Math Clip Art--Polygons--OctagonTopicGeometry Concepts DescriptionThis image shows two octagons: one regular and one irregular. An octagon is an eight-sided polygon. In a regular octagon, all sides and angles are equal, with each interior angle measuring 135 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular octagon, on the other hand, has sides and angles that are not all equal. This asymmetry means that the octagon can have a variety of shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
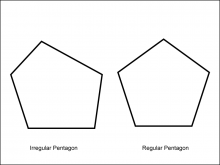
Math Clip Art--Geometry Concepts--Polygons--Pentagon | Math Clip Art--Polygons--PentagonTopicGeometry Concepts DescriptionThis image depicts two pentagons: one regular and one irregular. A pentagon is a five-sided polygon. In a regular pentagon, all sides and angles are equal, with each interior angle measuring 108 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular pentagon, however, has sides and angles that are not all equal. This asymmetry allows the pentagon to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
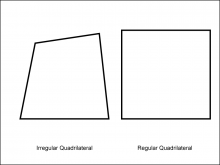
Math Clip Art--Geometry Concepts--Polygons--Quadrilateral | Math Clip Art--Polygons--QuadrilateralTopicGeometry Concepts DescriptionThis image illustrates two quadrilaterals: one regular and one irregular. A quadrilateral is a four-sided polygon. In a regular quadrilateral, such as a square, all sides and angles are equal, with each interior angle measuring 90 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular quadrilateral, however, has sides and angles that are not all equal. This asymmetry allows the quadrilateral to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |
|
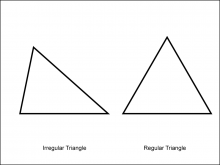
Math Clip Art--Geometry Concepts--Polygons--Triangle | Math Clip Art--Polygons--TriangleTopicGeometry Concepts DescriptionThis image shows two triangles: one regular and one irregular. A triangle is a three-sided polygon. In a regular triangle, also known as an equilateral triangle, all sides and angles are equal, with each interior angle measuring 60 degrees. This regularity gives it a symmetrical and balanced appearance. An irregular triangle, however, has sides and angles that are not all equal. This asymmetry allows the triangle to take on various shapes, depending on the specific lengths and angles of its sides. |
Definition of a Polygon |

|
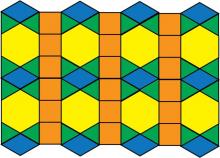
Math Clip Art--Geometry Concepts--Tessellation Pattern 2 | Math Clip Art--Tessellation Pattern 2TopicGeometry Concepts DescriptionThis image presents another tessellation pattern using basic shapes from pattern blocks. The basic pattern block shapes include equilateral triangles, squares, rhombuses, trapezoids, hexagons, and parallelograms. They are arranged to cover a plane without gaps or overlaps, demonstrating the principles of tessellation. Tessellations with pattern blocks help students explore geometric concepts such as symmetry, transformations, and tiling. They provide a visual and interactive way to understand how shapes can be combined to create complex patterns. |
Geometric Constructions with Polygons |
|
Math Clip Art--Geometry Concepts--Tessellation Pattern 3 | Math Clip Art--Tessellation Pattern 3TopicGeometry Concepts DescriptionThis image displays a tessellation pattern created with basic shapes from pattern blocks. The basic pattern block set includes equilateral triangles, squares, rhombuses, trapezoids, hexagons, and parallelograms. These shapes are arranged to tile a plane without gaps or overlaps. Using pattern blocks for tessellations allows students to explore geometric concepts such as symmetry, transformations, and spatial reasoning. They provide a hands-on approach to understanding how different shapes can be combined to form intricate patterns. |
Geometric Constructions with Polygons |
|
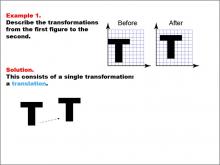
Math Example--Geometric Transformation--Transformations: Example 1 | Math Example--Geometric Transformation--Transformations: Example 1TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two "T" shapes are shown on a grid, labeled "Before" and "After". The "Before" shape on the left is translated to become the "After" shape on the right, illustrating how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
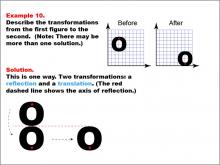
Math Example--Geometric Transformation--Transformations: Example 10 | Math Example--Geometric Transformation--Transformations: Example 10TopicTransformations DescriptionThis example showcases a combination of reflection and translation in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". A red dashed line indicates the axis of reflection. The transformation involves first reflecting the shape across this axis and then translating it to a new position. This demonstrates how multiple transformations can be applied in sequence to create more complex movements. |
Definition of Transformations |
|
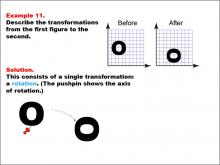
Math Example--Geometric Transformation--Transformations: Example 11 | Math Example--Geometric Transformation--Transformations: Example 11TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. Two circular "O" shapes are shown on a grid, one labeled "Before" and the other "After". The shape undergoes a rotation around a point indicated by a pushpin, which serves as the axis of rotation. This illustrates how an object can change its orientation without altering its size or position relative to the rotation point. |
Definition of Transformations |
|
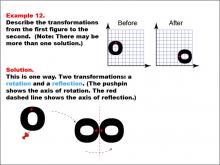
Math Example--Geometric Transformation--Transformations: Example 12 | Math Example--Geometric Transformation--Transformations: Example 12TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". The transformation involves two steps: first, a rotation around a point indicated by a pushpin, which serves as the axis of rotation, followed by a reflection across a red dashed line representing the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
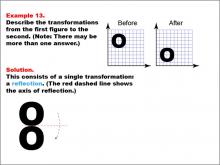
Math Example--Geometric Transformation--Transformations: Example 13 | Math Example--Geometric Transformation--Transformations: Example 13TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. Two grids are shown with the letter "O" before and after a transformation. The "Before" grid has the "O" on the left side, while the "After" grid has it on the right side. A red dashed line indicates the axis of reflection in the middle of the two "O"s. Below, there is a diagram showing the reflection transformation along this axis, illustrating how the shape is flipped across the line while maintaining its size and shape. |
Definition of Transformations |
|
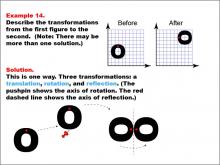
Math Example--Geometric Transformation--Transformations: Example 14 | Math Example--Geometric Transformation--Transformations: Example 14TopicTransformations DescriptionThis example illustrates a complex combination of transformations: translation, rotation, and reflection. Two grids are shown with an "O" shape before and after transformations. The "Before" grid has an "O" with a red dot at its center, while the "After" grid shows the same "O" but rotated and reflected. Below, a step-by-step diagram illustrates three sequential transformations: first, a translation moves the shape, then a rotation turns it around a pushpin (indicating the axis of rotation), and finally, a reflection flips it across a red dashed line. |
Definition of Transformations |
|
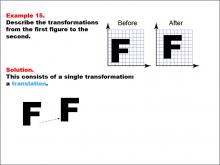
Math Example--Geometric Transformation--Transformations: Example 15 | Math Example--Geometric Transformation--Transformations: Example 15TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two grids are displayed with the letter "F" before and after a transformation. The "Before" grid shows an "F" on the left side, and the "After" grid shows it on the right side. Below, there is an arrow indicating that only a translation occurred between the two positions of the letter, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
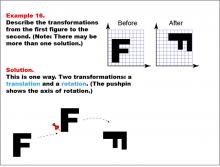
Math Example--Geometric Transformation--Transformations: Example 16 | Math Example--Geometric Transformation--Transformations: Example 16TopicTransformations DescriptionThis example demonstrates a combination of translation and rotation in geometric transformations. Two grids are shown with the letter "F" before and after transformations. The "Before" grid has an upright "F", while the "After" grid shows it rotated 90 degrees clockwise. Below, there is a diagram illustrating two steps: first, a translation moves the shape, then a rotation turns it around a pushpin axis. |
Definition of Transformations |

|
Math Example--Geometric Transformation--Transformations: Example 17 | Math Example--Geometric Transformation--Transformations: Example 17TopicTransformations DescriptionThis example illustrates a combination of reflection and translation in geometric transformations. The image shows a large letter "F" on a grid transforming into a letter "L". The transformation involves two steps: first, a reflection across an axis represented by a red dashed line, and then a translation to a new position. |
Definition of Transformations |
|
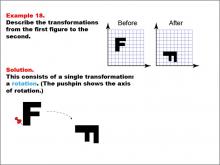
Math Example--Geometric Transformation--Transformations: Example 18 | Math Example--Geometric Transformation--Transformations: Example 18TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows the letter "F" on a grid being rotated to form the same letter in a different orientation. A pushpin indicates the axis of rotation, and an arrow shows the direction of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
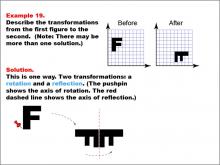
Math Example--Geometric Transformation--Transformations: Example 19 | Math Example--Geometric Transformation--Transformations: Example 19TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows the letter "F" being transformed into an upside-down version of itself. This transformation involves two steps: first, a rotation around an axis indicated by a pushpin, followed by a reflection across a line represented by a red dashed line. |
Definition of Transformations |
|
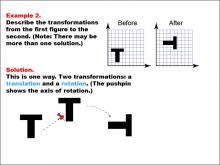
Math Example--Geometric Transformation--Transformations: Example 2 | Math Example--Geometric Transformation--Transformations: Example 2TopicTransformations DescriptionThis example illustrates a combination of transformations: translation and rotation. Two "T" shapes are shown on a grid, labeled "Before" and "After". The shape undergoes a translation (movement) and a rotation, with a pushpin indicating the axis of rotation. This demonstrates how multiple transformations can be applied sequentially to a shape. |
Definition of Transformations |
|
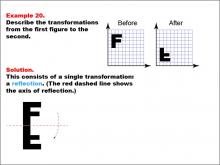
Math Example--Geometric Transformation--Transformations: Example 20 | Math Example--Geometric Transformation--Transformations: Example 20TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows the letter "F" being reflected to form the letter "L". A red dashed line indicates the axis of reflection, illustrating how the letter changes its orientation through this single transformation. This showcases how an object can be flipped over a line while changing its shape and orientation. |
Definition of Transformations |
|
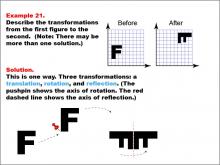
Math Example--Geometric Transformation--Transformations: Example 21 | Math Example--Geometric Transformation--Transformations: Example 21TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows an uppercase letter "F" on a grid labeled "Before" and a transformed version of the letter "F" upside down on another grid labeled "After." Below, there are illustrations showing the three steps of the transformation process. |
Definition of Transformations |
|
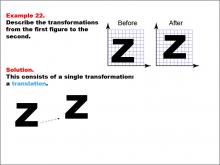
Math Example--Geometric Transformation--Transformations: Example 22 | Math Example--Geometric Transformation--Transformations: Example 22TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a horizontally shifted version of the same letter on another grid labeled "After." Below, there is an illustration showing just a translation, indicating that the letter "Z" is moved horizontally without any rotation or reflection. |
Definition of Transformations |
|
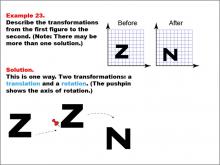
Math Example--Geometric Transformation--Transformations: Example 23 | Math Example--Geometric Transformation--Transformations: Example 23TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and an uppercase letter "N" on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first a translation (moving the figure) followed by a rotation (turning the figure). A pushpin indicates the axis of rotation. |
Definition of Transformations |
|
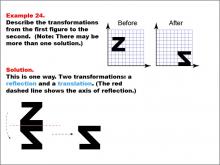
Math Example--Geometric Transformation--Transformations: Example 24 | Math Example--Geometric Transformation--Transformations: Example 24TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a rotated and translated version of the same letter in another position on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first, a reflection (flipping the figure across an axis shown by the red dashed line) and then a translation (moving the figure). |
Definition of Transformations |
|
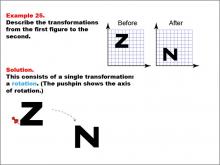
Math Example--Geometric Transformation--Transformations: Example 25 | Math Example--Geometric Transformation--Transformations: Example 25TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a transformation of the letter "Z" from an upright position to a rotated position resembling "N". The grid background helps visualize the transformation, and a pushpin icon indicates the axis of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
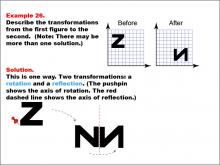
|
Math Example--Geometric Transformation--Transformations: Example 26 | Math Example--Geometric Transformation--Transformations: Example 26TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows a transformation of the letter "Z" into an upside-down "N". A pushpin indicates the axis of rotation, and a red dashed line represents the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
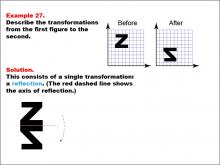
Math Example--Geometric Transformation--Transformations: Example 27 | Math Example--Geometric Transformation--Transformations: Example 27TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows a reflection of the letter "Z" across a horizontal red dashed line, resulting in a backward "Z". The grid background helps visualize the reflection, illustrating how an object can be flipped over a line while maintaining its size and shape but changing its orientation. |
Definition of Transformations |
|
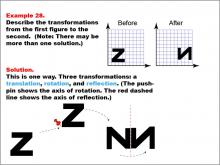
Math Example--Geometric Transformation--Transformations: Example 28 | Math Example--Geometric Transformation--Transformations: Example 28TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows a transformation of the letter "Z" into an upside-down "N". This transformation involves three steps: first, a translation moves the shape, then a rotation turns it (indicated by a pushpin showing the axis of rotation), and finally, a reflection flips it across a red dashed line representing the axis of reflection. |
Definition of Transformations |
|
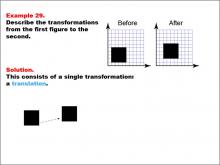
Math Example--Geometric Transformation--Transformations: Example 29 | Math Example--Geometric Transformation--Transformations: Example 29TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows a "Before" and "After" transformation of a black square on a grid. The square moves horizontally to the right, and a dotted arrow indicates the direction of movement. This showcases how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
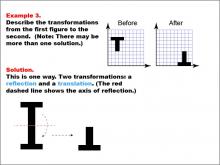
Math Example--Geometric Transformation--Transformations: Example 3 | Math Example--Geometric Transformation--Transformations: Example 3TopicTransformations DescriptionThis example showcases a combination of reflection and translation in geometric transformations. Two "T" shapes are displayed on a grid, labeled "Before" and "After". The shape is first reflected across a red dashed line (the axis of reflection) and then translated to a new position. This demonstrates how multiple transformations can be applied in sequence to create more complex movements. |
Definition of Transformations |
|
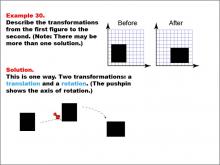
Math Example--Geometric Transformation--Transformations: Example 30 | Math Example--Geometric Transformation--Transformations: Example 30TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image depicts a "Before" and "After" transformation of a black square on a grid. The square moves down and rotates 90 degrees clockwise. A pushpin marks the axis of rotation, and dotted arrows indicate the movement and rotation. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
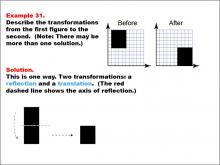
Math Example--Geometric Transformation--Transformations: Example 31 | Math Example--Geometric Transformation--Transformations: Example 31TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows a "Before" and "After" transformation of a black rectangle on a grid. The rectangle first reflects across a horizontal axis, marked by a red dashed line, and then translates horizontally to the right. This illustrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
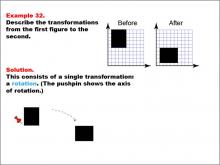
Math Example--Geometric Transformation--Transformations: Example 32 | Math Example--Geometric Transformation--Transformations: Example 32TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a "Before" and "After" transformation of a black rectangle on a grid. The rectangle rotates 90 degrees clockwise around an axis marked by a pushpin. This illustrates how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
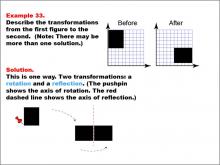
Math Example--Geometric Transformation--Transformations: Example 33 | Math Example--Geometric Transformation--Transformations: Example 33TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows a transformation of a black L-shaped figure on a grid. The "Before" figure is at the top left, and the "After" figure is at the top right. Below, there is a sequence of two transformations: first, a rotation (indicated by a pushpin showing the axis of rotation), followed by a reflection (shown by a red dashed line representing the axis of reflection). |
Definition of Transformations |
|
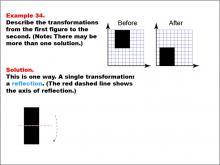
Math Example--Geometric Transformation--Transformations: Example 34 | Math Example--Geometric Transformation--Transformations: Example 34TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows a black L-shaped figure on a grid. The "Before" figure is at the top left, and the "After" figure is at the top right. Below, there is a single transformation: a reflection across a vertical axis shown with a red dashed line. This showcases how an object can be flipped over a line while maintaining its size and shape but changing its orientation. |
Definition of Transformations |
|
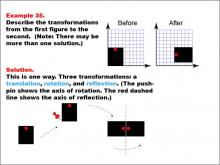
Math Example--Geometric Transformation--Transformations: Example 35 | Math Example--Geometric Transformation--Transformations: Example 35TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows a black L-shaped figure with a red dot on a grid. The "Before" figure is at the top left, and the "After" figure is at the top right. Below, there are three transformations: first, a translation moves the shape, then a rotation turns it around an axis shown by a pushpin, and finally, a reflection flips it across an axis shown by a red dashed line. |
Definition of Transformations |
|
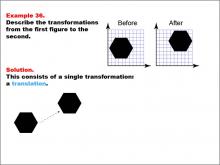
Math Example--Geometric Transformation--Transformations: Example 36 | Math Example--Geometric Transformation--Transformations: Example 36TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows two hexagons on grids. The "Before" figure is at the top left, and the "After" figure is at the top right. Below, there is a single transformation: translation, as indicated by an arrow showing movement from one position to another. This showcases how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
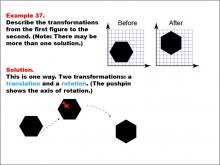
Math Example--Geometric Transformation--Transformations: Example 37 | Math Example--Geometric Transformation--Transformations: Example 37TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows a hexagon on a grid, with a "Before" and "After" transformation. The pushpin indicates the axis of rotation, and the hexagon is translated and rotated. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
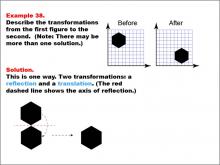
Math Example--Geometric Transformation--Transformations: Example 38 | Math Example--Geometric Transformation--Transformations: Example 38TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows a hexagon on a grid, with a "Before" and "After" transformation. A red dashed line shows the axis of reflection, followed by a translation. This illustrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
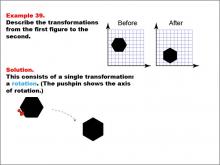
Math Example--Geometric Transformation--Transformations: Example 39 | Math Example--Geometric Transformation--Transformations: Example 39TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a hexagon on a grid, with a "Before" and "After" transformation. A pushpin indicates the axis of rotation, and only one transformation occurs. This illustrates how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
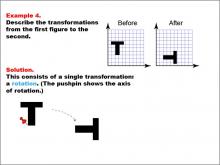
Math Example--Geometric Transformation--Transformations: Example 4 | Math Example--Geometric Transformation--Transformations: Example 4TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. Two "T" shapes are shown on a grid, labeled "Before" and "After". The shape undergoes a rotation around a point indicated by a pushpin, which serves as the axis of rotation. This illustrates how an object can change its orientation without altering its size or position relative to the rotation point. |
Definition of Transformations |