Illustrative Math Alignment: Grade 8 Unit 9

Putting It All Together

Lesson 2: Regular Tessellations

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
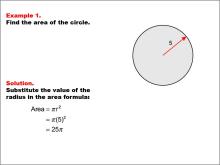
Math Examples Collection: Circular Area and Circumference	Overview This collection aggregates all the math examples around the topic of Circular Area and Circumference. There are a total of 23 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.	Area and Circumference
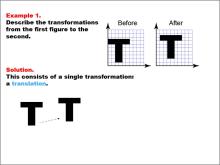
Math Examples Collection: Transformations	Overview The Transformations collection on Media4Math offers a comprehensive set of 56 math examples, providing educators with a rich resource for teaching geometric transformations. This collection covers a wide range of skills and concepts related to transformations, including translations, reflections, rotations, and dilations.	Definition of Transformations
Math Video Collection: Geometry Applications Video Series: Circles	Overview This collection aggregates all the math videos and resources in this series: Geometry Applications Video Series: Circles. There are a total of 13 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.	Applications of Circles and Definition of a Circle
Math Video Collection: Geometry Applications Video Series: Transformations	Overview This collection aggregates all the math videos and resources in this series: Geometry Applications Video Series: Transformations. There are a total of 12 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.	Applications of Transformations and Definition of Transformations
Math Definitions Collection: Circles	Overview The collection of definitions on the topic of circles provided by Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as radius, diameter, circumference, chord, and tangent, each explained with clarity and precision. Understanding these fundamental concepts is crucial for students as they form the building blocks for more advanced studies in geometry and algebra.	Definition of a Circle
Closed Captioned Video: Geometry Applications: Area and Volume, 2	Closed Captioned Video: Geometry Applications: Area and Volume, 2 Topic Area and Volume Description This segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency.	Applications of Surface Area and Volume, Surface Area and Volume
Closed Captioned Video: Geometry Applications: Transformations	Closed Captioned Video: Geometry Applications: Transformations Topic Transformations	Definition of Transformations and Applications of Transformations
Closed Captioned Video: Geometry Applications: Transformations, 1	Closed Captioned Video: Geometry Applications: Transformations, 1 Topic Transformations Description Explores translations and rotations in motion, using roller coasters as an example. Key concepts include displacement vectors, magnitude, and direction, modeled geometrically and computationally for practical applications in physics and engineering. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields.	Definition of Transformations and Applications of Transformations
Closed Captioned Video: Geometry Applications: Transformations, 2	Closed Captioned Video: Geometry Applications: Transformations, 2 Topic Transformations Description This segment applies 3D translations to logistics, focusing on container arrangement in shipping. Using coordinate systems, it demonstrates efficiency in loading/unloading cargo, leveraging geometric organization and data sorting methods for real-world impact. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields.	Definition of Transformations and Applications of Transformations
Closed Captioned Video: Geometry Applications: Transformations, 3	Closed Captioned Video: Geometry Applications: Transformations, 3 Topic Transformations Description Analyzes observatory designs and their use of rotational and reflective symmetry for astronomical viewing. The segment models celestial movements and applies rotational geometry concepts to optimize the structure’s functionality. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields.	Definition of Transformations and Applications of Transformations
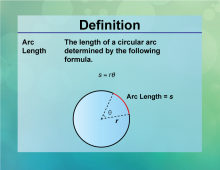
Definition--Circle Concepts--Arc Length	Arc Length Topic Circles Definition An arc length is the distance along the curved line making up the arc. Description The arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula L = rθ	Definition of a Circle
Definition--Circle Concepts--Area of a Circle	Area of a Circle Topic Circles Definition The area of a circle is the space contained within its circumference, calculated as A = πr2 Description The area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula A = πr2	Definition of a Circle
Definition--Circle Concepts--Center of a Circle	Center of a Circle Topic Circles Definition The center of a circle is the point equidistant from all points on the circle. Description The center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation	Definition of a Circle
Definition--Circle Concepts--Chord	Chord Topic Circles Definition A chord is a line segment with both endpoints on the circle.	Definition of a Circle
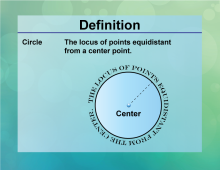
Definition--Circle Concepts--Circle	Circle Topic Circles Definition A circle is a set of all points in a plane equidistant from a given point, the center. Description The circle is one of the most fundamental shapes in geometry, characterized by its symmetry and uniformity. It is used extensively in various fields, including engineering, design, and astronomy, where its properties are applied to create wheels, gears, and orbits. Mathematically, a circle is defined by its center and radius, and its equation in a plane is (x − h)2 + (y − k)2 = r2	Definition of a Circle
Definition--Circle Concepts--Circle Inscribed in a Square	Circle Inscribed in a Square Topic Circles Definition A circle inscribed in a square touches all four sides of the square at exactly one point each.	Definition of a Circle
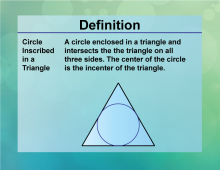
Definition--Circle Concepts--Circle Inscribed in a Triangle	Circle Inscribed in a Triangle Topic Circles Definition An inscribed circle in a triangle is tangent to each of the triangle's sides.	Definition of a Circle
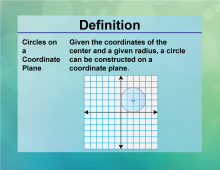
Definition--Circle Concepts--Circles on a Coordinate Plane	Circles on a Coordinate Plane Topic Circles Definition Circles on a coordinate plane are defined by their center coordinates and radius. Description Understanding circles on a coordinate plane is essential for analyzing geometric shapes in a mathematical context. This concept is widely used in computer graphics, navigation systems, and physics simulations, where precise positioning and movement of circular objects are required. The standard equation of a circle in the coordinate plane is (x − h)2 + (y − k)2 = r2	Definition of a Circle
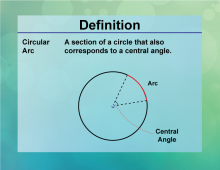
Definition--Circle Concepts--Circular Arc	Circular Arc Topic Circles Definition A circular arc is a portion of the circumference of a circle. Description Circular arcs are segments of a circle's circumference, used extensively in design, architecture, and engineering to create curved structures and paths. The length of an arc is determined by the central angle and the circle's radius, calculated using the formula L = rθ	Definition of a Circle
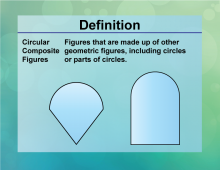
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
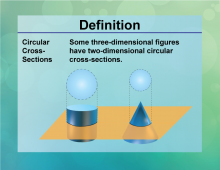
Definition--Circle Concepts--Circular Cross-Sections	Circular Cross-Sections Topic Circles Definition Circular cross-sections are the intersections of a plane with a solid that result in a circle.	Definition of a Circle
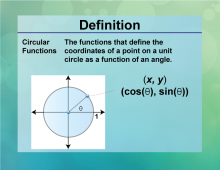
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
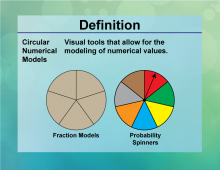
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
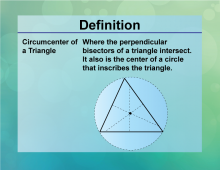
Definition--Circle Concepts--Circumcenter of Triangle	Circumcenter of Triangle Topic Circles Definition The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices.	Definition of a Circle
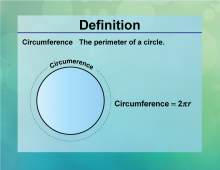
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
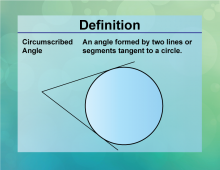
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Concentric Circles	Concentric Circles Topic Circles Definition Concentric circles are circles that share the same center but have different radii.	Definition of a Circle
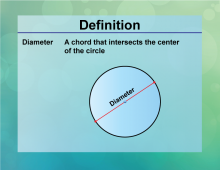
Definition--Circle Concepts--Diameter	Diameter Topic Circles Definition The diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. Description The diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
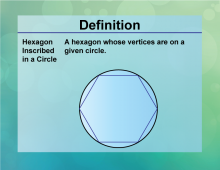
Definition--Circle Concepts--Hexagon Inscribed in a Circle	Hexagon Inscribed in a Circle Topic Circles Definition A hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle.	Definition of a Circle
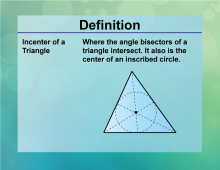
Definition--Circle Concepts--Incenter of a Triangle	Incenter of a Triangle Topic Circles Definition The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.	Definition of a Circle
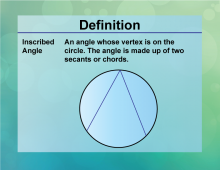
Definition--Circle Concepts--Inscribed Angle	Inscribed Angle Topic Circles Definition An inscribed angle is an angle formed by two chords in a circle that share an endpoint.	Definition of a Circle
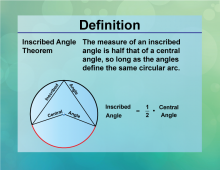
Definition--Circle Concepts--Inscribed Angle Theorem	Inscribed Angle Theorem Topic Circles Definition The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc.	Definition of a Circle
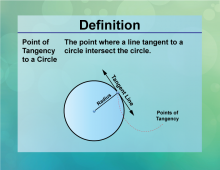
Definition--Circle Concepts--Point of Tangency to a Circle	Point of Tangency to a Circle Topic Circles Definition The point of tangency is the point where a tangent line touches the circle.	Definition of a Circle
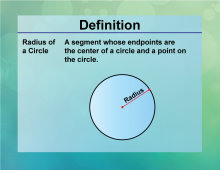
Definition--Circle Concepts--Radius of a Circle	Radius of a Circle Topic Circles Definition The radius of a circle is a line segment from the center to any point on the circle.	Definition of a Circle
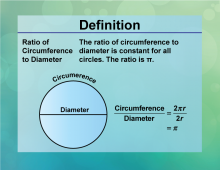
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
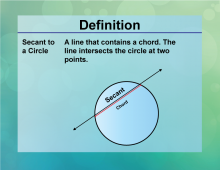
Definition--Circle Concepts--Secant to a Circle	Secant to a Circle Topic Circles Definition A secant is a line that intersects a circle at two points. Description Secants are significant in geometry, representing lines that intersect a circle at two distinct points. These lines are used in various applications, such as in design and architecture, where precise measurements of angles and distances are essential. In mathematics, secants are explored in the context of circle theorems, providing insights into the properties of lines and circles. In education, understanding secants helps students develop geometric reasoning and problem-solving skills, which are essential for advanced studies in geometry and trigonometry.	Definition of a Circle
Definition--Circle Concepts--Sector	Sector Topic Circles Definition A sector is a portion of a circle enclosed by two radii and the arc between them. Description Sectors are fundamental in the study of circles, representing a portion of the circle's area. These shapes are used in various applications, such as in design and architecture, where precise measurements of angles and areas are essential. The area of a sector is calculated using the formula A = 1/2r2θ	Definition of a Circle
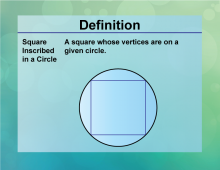
Definition--Circle Concepts--Square Inscribed in a Circle	Square Inscribed in a Circle Topic Circles Definition A square inscribed in a circle has its vertices touching the circle.	Definition of a Circle
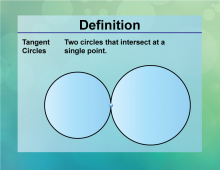
Definition--Circle Concepts--Tangent Circles	Tangent Circles Topic Circles Definition Tangent circles are two or more circles that intersect at exactly one point.	Definition of a Circle
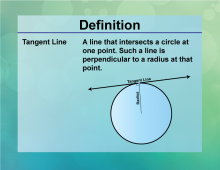
Definition--Circle Concepts--Tangent Line	Tangent Line Topic Circles Definition A tangent line is a straight line that touches a circle at exactly one point.	Definition of a Circle
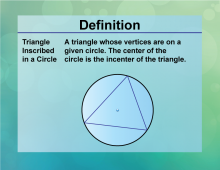
Definition--Circle Concepts--Triangle Inscribed in a Circle	Triangle Inscribed in a Circle Topic Circles Definition A triangle inscribed in a circle has its vertices on the circle.	Definition of a Circle
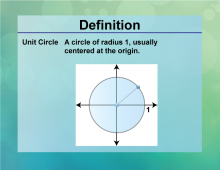
Definition--Circle Concepts--Unit Circle	Unit Circle Topic Circles Definition The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane.	Definition of a Circle
Instructional Resource--Geometric Construction--Constructing an Egg Shape	Instructional Resource \| Geometric Construction \| An Egg Shape In this instructional resource, we show the steps in constructing an egg shape. In the process, students learn about using common points of tangency to create smooth curves from two different shapes. This activity can be done with pencil, compass, ruler, and grid paper. —PRESS PREVIEW TO VIEW THE ACTIVITY— To see the complete collection of Instructional Resource, click on this link.	Geometric Constructions with Circles
INSTRUCTIONAL RESOURCE: Math Examples 1	INSTRUCTIONAL RESOURCE: Math Examples--Circular Area and Circumference This set of tutorials provides 23 examples of solving for the area and circumferences of circles and sections of circles. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Area and Circumference
Interactive Crossword Puzzle--Circles	Interactive Crossword Puzzle--Circles This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide. Related Resources To see additional resources on this topic, click on the Related Resources tab.	Definition of a Circle
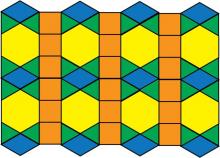
Math Clip Art--Geometry Concepts--Tessellation Pattern 2	Math Clip Art--Tessellation Pattern 2 Topic Geometry Concepts Description This image presents another tessellation pattern using basic shapes from pattern blocks. The basic pattern block shapes include equilateral triangles, squares, rhombuses, trapezoids, hexagons, and parallelograms. They are arranged to cover a plane without gaps or overlaps, demonstrating the principles of tessellation. Tessellations with pattern blocks help students explore geometric concepts such as symmetry, transformations, and tiling. They provide a visual and interactive way to understand how shapes can be combined to create complex patterns.	Geometric Constructions with Polygons
Math Clip Art--Geometry Concepts--Tessellation Pattern 3	Math Clip Art--Tessellation Pattern 3 Topic Geometry Concepts Description This image displays a tessellation pattern created with basic shapes from pattern blocks. The basic pattern block set includes equilateral triangles, squares, rhombuses, trapezoids, hexagons, and parallelograms. These shapes are arranged to tile a plane without gaps or overlaps. Using pattern blocks for tessellations allows students to explore geometric concepts such as symmetry, transformations, and spatial reasoning. They provide a hands-on approach to understanding how different shapes can be combined to form intricate patterns.	Geometric Constructions with Polygons
Math Example--Area and Perimeter--Circular Area and Circumference: Example 1	Math Example--Area and Perimeter--Circular Area and Circumference: Example 1 Topic Geometry Description This example presents a circle with a radius of 5 units. The task is to calculate the area of the circle using the given radius. The solution involves substituting the radius value into the area formula: A = π * r^2 = π * (5)^2 = 25π. Understanding circular area and circumference is integral to mastering geometry. Concepts such as calculating areas and circumferences of circles are fundamental, and exercises like these examples not only provide practice but also deepen the understanding of theoretical concepts in a practical way.	Area and Circumference