
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 10: Bases and Heights of Triangles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
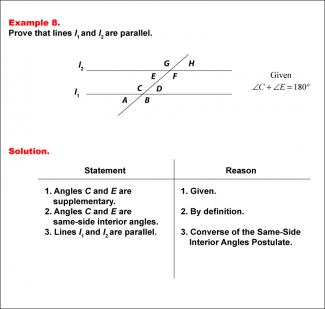
Math Example--Geometric Proofs--Example 8 |
Math Example--Geometric Proofs--Example 8
This is part of a collection of math examples that focus on geometric proofs. |
Parallel Lines and Definition of a Triangle |
|
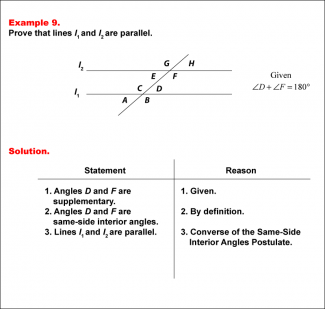
Math Example--Geometric Proofs--Example 9 |
Math Example--Geometric Proofs--Example 9
This is part of a collection of math examples that focus on geometric proofs. |
Parallel Lines and Definition of a Triangle |
|
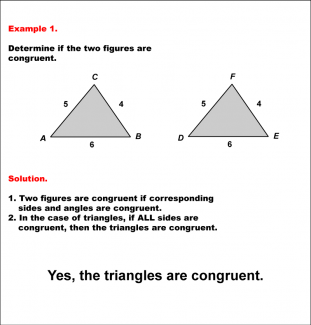
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
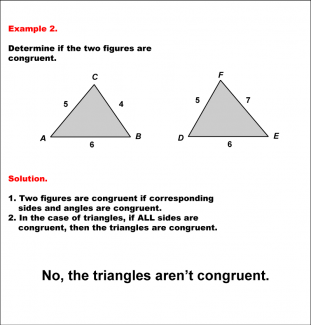
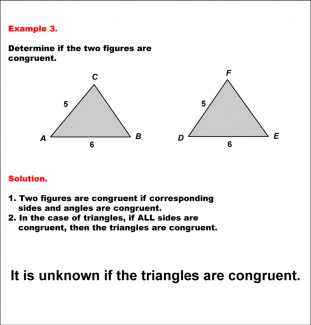
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
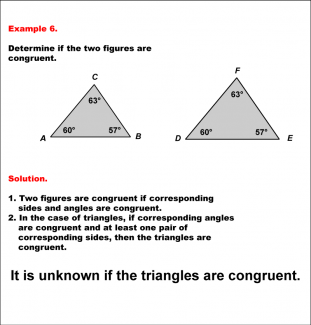
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
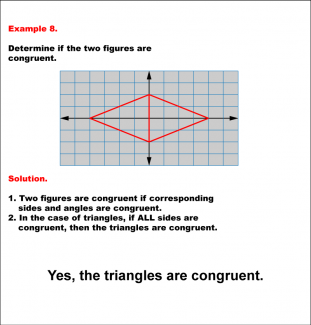
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
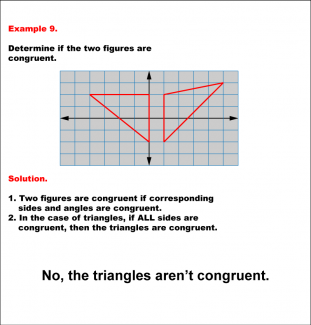
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 |
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
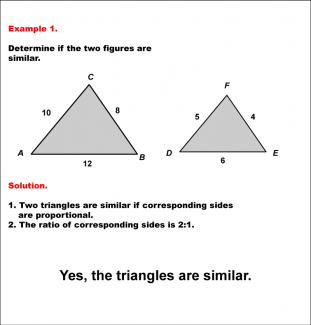
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 4, and 6. Triangles are similar if corresponding sides are proportional. Here, the ratio of corresponding sides is 2:1 (10:5, 8:4, 12:6). Thus, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has angle 40°, and the other triangle has a 60° angle. For similarity, all corresponding angles must be congruent. The angles in each triangle do not match, so the triangles aren't similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
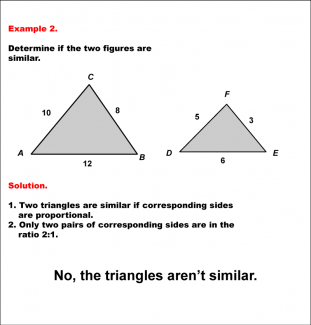
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 3, and 6. Triangles are similar if all corresponding sides are proportional. Only two pairs of sides here have a 2:1 ratio, so the triangles are not similar. Therefore, the answer is No, the triangles arenÕt similar. |
Definition of a Triangle |
|
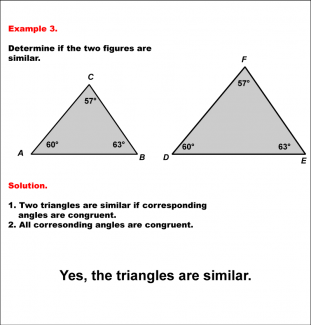
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Both triangles have angles 60°, 57°, and 63°. Triangles are similar if corresponding angles are equal. Since all corresponding angles match, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has angles 75°, 42°, and an unknown angle, and triangle DEF has angles 75° and 63° and an unknown angles. Triangles are similar if all corresponding angles are congruent. Solving for the unknown angles confirms angle congruency, so the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two right triangles, ABC and DEF, are similar. Triangle ABC has angles 90° and 40°, and triangle DEF has angles 90° and 50°. Triangles are similar if all corresponding angles are congruent. Solving reveals congruent corresponding angles. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has a right angle and an angle of 40°, and triangle DEF has a right angle and 45°. Not all corresponding angles are congruent, so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |
|
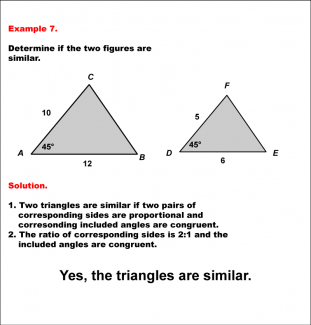
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 45° angle. Triangles are similar if two pairs of sides are proportional, and the included angle is congruent. The side ratio is 2:1, and both included angles are 45°. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |
|
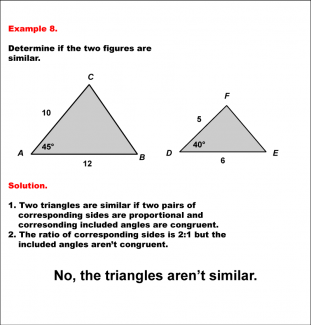
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 40° angle. Triangles are similar if two pairs of sides are proportional, and the included angles are congruent. Here, the included angles differ (45° vs. 40°), so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
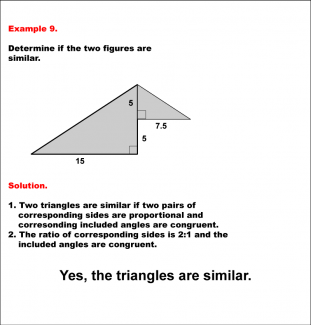
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9 |
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has sides 10 and 15 and an included right angle, while the other triangle has sides 5 and 7.5 and an included right angle. Triangles are similar if two pairs of corresponding sides are proportional, and corresponding included angles are congruent. The side ratio is 2:1, and the included right angles are congruent. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Congruent Triangles--Example 1 |
Math Example--Geometric Shapes--Congruent Triangles--Example 1TopicGeometry DescriptionThis image shows two triangles labeled ABC and DEF. The triangles are oriented differently but have corresponding sides and angles marked as congruent. The table below the triangles lists the congruent sides and angles. In this topic, students explore principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
|
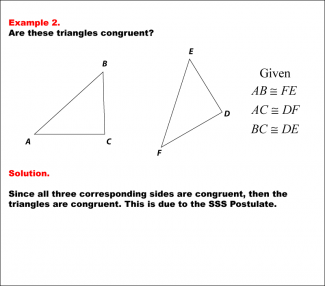
Math Example--Geometric Shapes--Congruent Triangles--Example 2 |
Math Example--Geometric Shapes--Congruent Triangles--Example 2TopicGeometry DescriptionThis image shows two triangles labeled ABC and DEF. The triangles are oriented differently, but the corresponding sides are marked as congruent. The given information lists AB ≅ FE, AC ≅ DF, and BC ≅ DE. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
|
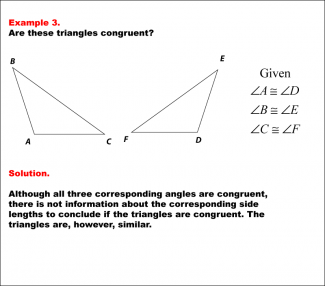
Math Example--Geometric Shapes--Congruent Triangles--Example 3 |
Math Example--Geometric Shapes--Congruent Triangles--Example 3TopicGeometry DescriptionThis image shows two triangles labeled ABC and DEF. The triangles have corresponding angles marked as congruent (∠A ≅ ∠D, ∠B ≅ ∠E, ∠C ≅ ∠F). However, no information is given about the side lengths. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
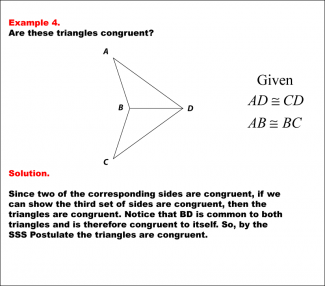
|
Math Example--Geometric Shapes--Congruent Triangles--Example 4 |
Math Example--Geometric Shapes--Congruent Triangles--Example 4TopicGeometry DescriptionThis image shows two triangles ABD and CBD sharing a common side BD. Given information includes AD ≅ CD and AB ≅ BC. The solution points out that BD is common to both triangles and uses this to conclude that the triangles are congruent by the SSS Postulate. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Congruent Triangles--Example 5 |
Math Example--Geometric Shapes--Congruent Triangles--Example 5TopicGeometry DescriptionThe image shows two triangles, each intersecting a circle at two points and one of whose angles is a central angle. The triangles are ABC and DCE. We are given that AB ≅ DE. Furthermore, each triangle has two sides that correspond to radii of the circle and therefore those sides are congruent. As a result of the SSS Postulate, since corresponding sides of the triangle are congruent, then the triangles are congruent. |
Definition of a Triangle |
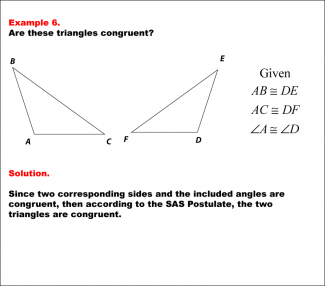
|
Math Example--Geometric Shapes--Congruent Triangles--Example 6 |
Math Example--Geometric Shapes--Congruent Triangles--Example 6TopicGeometry DescriptionThe image displays two triangles. The left triangle is labeled ABC. The right triangle is labeled DEF. We are given congruent corresponding sides and angles. Using the SAS Postulate, the two triangles are congruent. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
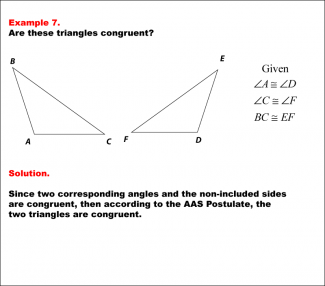
|
Math Example--Geometric Shapes--Congruent Triangles--Example 7 |
Math Example--Geometric Shapes--Congruent Triangles--Example 7TopicGeometry DescriptionThe image shows two triangles. The left triangle is labeled ABC . The right triangle is labeled DEF. We are given pairs of corresponding angles and corresponding sides. Using the AAS Postulate, we can prove the triangles are congruent. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
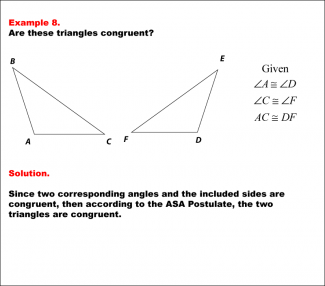
|
Math Example--Geometric Shapes--Congruent Triangles--Example 8 |
Math Example--Geometric Shapes--Congruent Triangles--Example 8TopicGeometry DescriptionThe image depicts two triangles. The left triangle is labeled ABC. The right triangle is labeled DEF. We are given pairs of corresponding angles and a pair of corresponding sides. Using the ASA Postulate, the two triangles are congruent. In this topic, students explore the principles of Geometry, particularly focusing on congruence in geometric shapes. Examples like this help build an understanding of how congruence is determined by matching angles and sides. |
Definition of a Triangle |
|
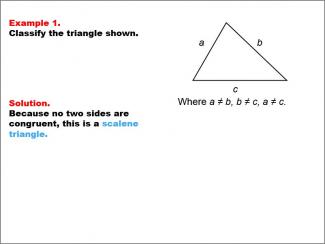
Math Example--Polygons--Triangle Classification: Example 1 |
Math Example--Polygons--Triangle Classification: Example 1TopicTriangles DescriptionThis image shows a triangle with side lengths labeled as a, b, and c, where all sides are unequal. Based on the length of each side, the triangle is classified as scalene, as no two sides are congruent. Triangles are categorized based on side length (scalene, isosceles, equilateral) or angle measures (acute, obtuse, right). In this example, the scalene classification is determined by identifying that each side is a different length. The examples in this collection illustrate various classification rules based on both side and angle properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 10 |
Math Example--Polygons--Triangle Classification: Example 10TopicTriangles DescriptionThis example presents a triangle with side lengths of 10, 10, and 8. Since two sides are congruent, the triangle is classified as isosceles. Triangle classification can be determined by side lengths or angle measures. Isosceles triangles have two equal sides or angles. Reviewing different examples assists students in identifying these types based on side or angle properties. Seeing multiple worked-out examples reinforces students’ ability to classify triangles by consistently applying classification rules. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 11 |
Math Example--Polygons--Triangle Classification: Example 11TopicTriangles DescriptionThis example shows a triangle with two sides labeled as x and a third side labeled y. Because two sides are congruent, the triangle is classified as isosceles. Triangles can be classified by their side lengths or angle measures. An isosceles triangle has two equal sides or angles, as seen in this example. Reviewing a series of examples helps students understand these classifications and recognize patterns in triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 12 |
Math Example--Polygons--Triangle Classification: Example 12TopicTriangles DescriptionThis example shows a triangle with side lengths all equal to 9. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be classified based on side or angle properties. An equilateral triangle has all sides and angles congruent. Viewing multiple examples reinforces students’ understanding of these classifications and enhances their ability to recognize triangle properties. Seeing several worked-out examples helps students understand and apply the rules consistently for classifying triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 13 |
Math Example--Polygons--Triangle Classification: Example 13TopicTriangles DescriptionThis example shows a triangle with three sides labeled as x, all equal in length. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be categorized by side length or angle measures. An equilateral triangle has all congruent sides and angles. Reviewing multiple examples helps students recognize triangle classifications by observing side and angle patterns. Providing several examples reinforces students’ ability to consistently classify triangles based on the observed properties. |
Definition of a Triangle |
|
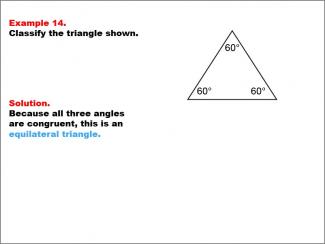
Math Example--Polygons--Triangle Classification: Example 14 |
Math Example--Polygons--Triangle Classification: Example 14TopicTriangles DescriptionThis example shows a triangle with three angles, each measuring 60°. Since all angles are equal, the triangle is classified as equilateral. Triangle classification can be based on side lengths or angle measures. An equilateral triangle has all angles congruent. Reviewing examples like these helps students understand classification rules based on triangle properties. Multiple examples reinforce students' ability to identify triangle types consistently by observing angle or side characteristics. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 15 |
Math Example--Polygons--Triangle Classification: Example 15TopicTriangles DescriptionThis example presents a triangle with two angles labeled 60° and an unknown angle labeled x. Solving for x, we find it to be 60°, making all angles congruent and classifying the triangle as equilateral. Triangle classification can be determined by side length or angle measures. An equilateral triangle has all equal sides and angles. Observing multiple examples helps students apply these criteria consistently when classifying triangles. Seeing several worked examples helps students gain confidence in identifying triangles by recognizing congruent angles or sides. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 16 |
Math Example--Polygons--Triangle Classification: Example 16TopicTriangles DescriptionThis example presents a triangle with three sides labeled as x, each equal in length. Since all three sides are congruent, the triangle is classified as equilateral. Triangles are categorized by their side lengths or angle measures. An equilateral triangle has all equal sides and angles, as seen in this example. Reviewing multiple examples reinforces students' understanding of the consistent characteristics that define each triangle type. Providing multiple worked-out examples helps students confidently apply classification rules to identify triangles by their properties. |
Definition of a Triangle |
|
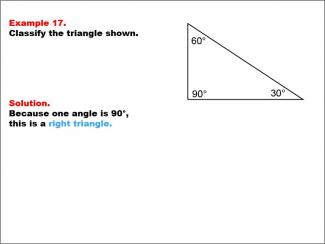
Math Example--Polygons--Triangle Classification: Example 17 |
Math Example--Polygons--Triangle Classification: Example 17TopicTriangles DescriptionThis example shows a triangle with angles measuring 90°, 60°, and 30°. Since one angle is exactly 90°, the triangle is classified as a right triangle. Triangle classification often considers angle measures, with right triangles defined by having one 90° angle. Observing multiple examples allows students to consistently apply this classification rule. Reviewing various worked-out examples helps students solidify their understanding of identifying triangle types based on angle measurements. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 18 |
Math Example--Polygons--Triangle Classification: Example 18TopicTriangles DescriptionThis example shows a triangle with two angles labeled 50° and 40° and an unknown angle x. Solving for x, we find it to be 90°, which classifies this as a right triangle. Triangles are classified by side lengths or angles, and a right triangle has a 90° angle. Examining examples like this helps students reinforce the criteria for identifying right triangles based on their angle properties. Seeing multiple worked-out examples enables students to apply classification rules more effectively and confidently. |
Definition of a Triangle |
|
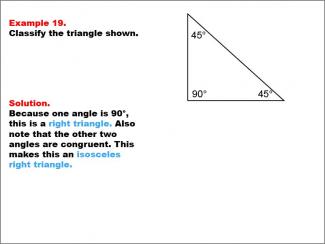
Math Example--Polygons--Triangle Classification: Example 19 |
Math Example--Polygons--Triangle Classification: Example 19TopicTriangles DescriptionThis example presents a triangle with two congruent angles of 45° and one right angle of 90°. Because it has a 90° angle, the triangle is classified as a right triangle, and the two equal angles make it an isosceles right triangle. Triangle classification can involve side lengths or angles. A right triangle has a 90° angle, while isosceles triangles have two equal angles or sides. This example combines both classifications. Reviewing multiple examples helps students confidently apply the criteria to identify triangle types. |
Definition of a Triangle |
|
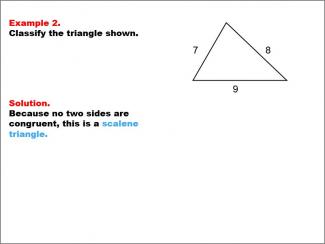
Math Example--Polygons--Triangle Classification: Example 2 |
Math Example--Polygons--Triangle Classification: Example 2TopicTriangles DescriptionThis image shows a triangle with sides measuring 7, 8, and 9. The triangle is classified as scalene because each side has a different length, meaning no two sides are congruent. Triangles can be classified by examining their side lengths or angle measures. Scalene triangles, like the one shown, have no congruent sides, making them unique. This collection of examples helps students understand classification rules and visually identify different triangle types. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 20 |
Math Example--Polygons--Triangle Classification: Example 20TopicTriangles DescriptionThis example shows a triangle with two known angles of 45° and an unknown angle x. Solving for x, we find it to be 90°, classifying this as a right triangle with two congruent angles, making it an isosceles right triangle. Triangle classification may be based on side lengths or angles. Right triangles have a 90° angle, while isosceles triangles have two equal sides or angles. Examples like this help students understand combined classifications. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 21 |
Math Example--Polygons--Triangle Classification: Example 21TopicTriangles DescriptionThis example shows a triangle with angles labeled as x, 2x, and 3x. Solving for x, we find that the angles are 30°, 60°, and 90°, classifying it as a right triangle. Triangle classification can involve angle measures or side lengths. Right triangles have one 90° angle, as seen here. Reviewing various examples supports students in consistently applying these classification rules. Observing multiple worked-out examples helps students gain confidence in identifying triangles based on the presence of specific angle measures. |
Definition of a Triangle |
|
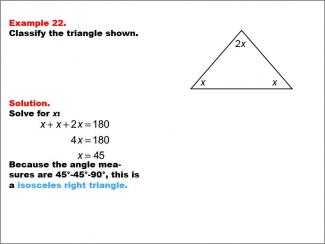
Math Example--Polygons--Triangle Classification: Example 22 |
Math Example--Polygons--Triangle Classification: Example 22TopicTriangles DescriptionThis example shows a triangle with two equal angles labeled x and a third angle labeled 2x. Solving for x, we find the angles to be 45°, 45°, and 90°, classifying it as an isosceles right triangle. Triangles are classified by their angle measures or side lengths. Right triangles have a 90° angle, and isosceles triangles have two congruent angles. Reviewing examples like this one helps students understand combined classifications. |
Definition of a Triangle |
|
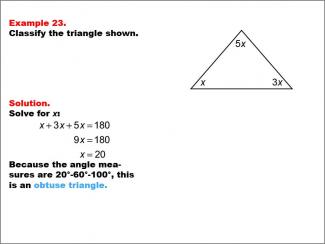
Math Example--Polygons--Triangle Classification: Example 23 |
Math Example--Polygons--Triangle Classification: Example 23TopicTriangles DescriptionThis example shows a triangle with angles labeled x, 3x, and 5x. Solving for x, we find the angles to be 20°, 60°, and 100°, which classifies this triangle as obtuse because one of the angles is greater than 90°. Triangles can be classified by angle measures, with obtuse triangles defined as having one angle greater than 90°. Observing examples like this aids students in understanding how angle measures determine classifications. Providing multiple worked-out examples reinforces students' ability to consistently classify triangles based on angle properties. |
Definition of a Triangle |
|
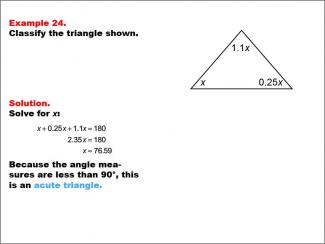
Math Example--Polygons--Triangle Classification: Example 24 |
Math Example--Polygons--Triangle Classification: Example 24TopicTriangles DescriptionThis example shows a triangle with angles labeled as x, 0.25x, and 1.1x. Solving for x, we find that all angles are less than 90°, classifying the triangle as acute. Triangles are classified by their angle measures or side lengths, with acute triangles having all angles less than 90°. Reviewing examples like this helps students reinforce the criteria for classifying triangles based on angle sizes. Seeing multiple worked-out examples builds students' confidence in applying classification rules and identifying triangle types based on consistent properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 3 |
Math Example--Polygons--Triangle Classification: Example 3TopicTriangles DescriptionThis example shows a triangle with side lengths of 12, 18, and x, where x is not equal to 12 or 18. The triangle is classified as scalene because all three side lengths are different. Triangles are categorized by side length or angle. Scalene triangles, with all sides unequal, demonstrate a key classification type. Multiple examples help students recognize classification patterns for triangles based on side length or angle measure. Observing various worked-out examples reinforces consistent application of classification criteria, building student confidence in identifying triangle types. |
Definition of a Triangle |
|
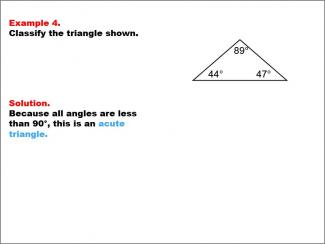
Math Example--Polygons--Triangle Classification: Example 4 |
Math Example--Polygons--Triangle Classification: Example 4TopicTriangles DescriptionThis example displays a triangle with angles measuring 89°, 44°, and 47°. Since all angles are less than 90°, the triangle is classified as acute. Triangle classification can be based on side length or angle measures. Acute triangles have all angles less than 90°, as shown in this example. Reviewing multiple examples in this way helps students visually distinguish triangle types by angle. Providing varied worked-out examples solidifies students’ understanding of the criteria for each triangle type, enabling them to accurately identify triangles by their angle measures. |
Definition of a Triangle |
|
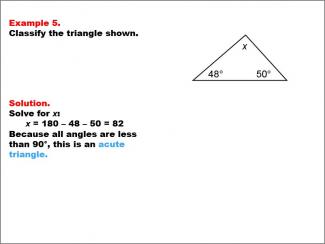
Math Example--Polygons--Triangle Classification: Example 5 |
Math Example--Polygons--Triangle Classification: Example 5TopicTriangles DescriptionThis example presents a triangle with angles of 48°, 50°, and an unknown angle x. Solving for x, we find that x = 82°, meaning all angles are less than 90°, classifying it as acute. Triangles can be identified by their angles or side lengths. Acute triangles have all angles less than 90°, as seen here. Reviewing examples like this supports student understanding of angle-based classification. Seeing multiple worked examples helps students recognize patterns and confidently classify triangles based on established criteria. |
Definition of a Triangle |
|
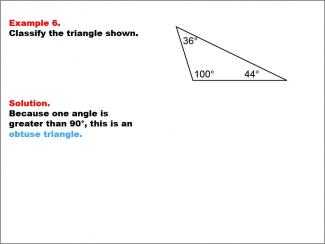
Math Example--Polygons--Triangle Classification: Example 6 |
Math Example--Polygons--Triangle Classification: Example 6TopicTriangles DescriptionThis example shows a triangle with angles of 36°, 100°, and 44°. Because one of the angles is greater than 90°, this triangle is classified as obtuse. Triangles are classified by side lengths or angles. An obtuse triangle has one angle greater than 90°, as seen here. This collection of examples supports students in identifying and classifying triangles based on distinct angle measures. Seeing multiple worked-out examples reinforces students' understanding of classification rules, making it easier to recognize triangle types based on angle or side length. |
Definition of a Triangle |