
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 10: Bases and Heights of Triangles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
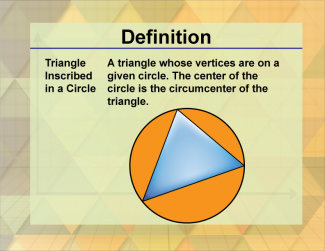
Definition--Triangle Concepts--Inscribed Triangle |
Inscribed TriangleTopicTriangles DefinitionAn inscribed triangle is a triangle that is drawn inside a circle, with all its vertices touching the circle. DescriptionAn inscribed triangle, also known as a circumtriangle, is a triangle that is drawn inside a circle, with all its vertices touching the circle. The circle is called the circumcircle, and its center is the circumcenter of the triangle. |
Definition of a Triangle |
|
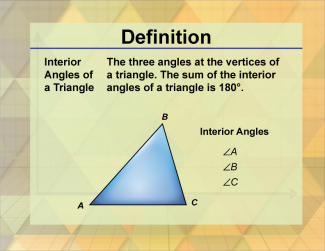
Definition--Triangle Concepts--Interior Angles of a Triangle |
Interior Angles of a TriangleTopicTriangles DefinitionThe interior angles of a triangle are the angles inside the triangle, and their sum is always 180 degrees. DescriptionThe interior angles of a triangle are a fundamental concept in geometry, representing the angles inside the triangle. The sum of the interior angles of any triangle is always 180 degrees, which is a crucial property used in various geometric proofs and constructions. |
Definition of a Triangle |
|
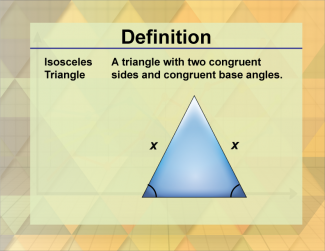
Definition--Triangle Concepts--Isosceles Triangle, Definition 1 |
Isosceles Triangle, Definition 1TopicTriangles DefinitionAn isosceles triangle is a triangle with at least two sides of equal length. DescriptionAn isosceles triangle is a type of triangle that has at least two sides of equal length. This property gives the isosceles triangle its unique characteristics, such as having two equal angles opposite the equal sides. This concept is significant in various real-world applications, such as in design and architecture, where symmetry and balance are important. For example, understanding the properties of isosceles triangles helps in creating aesthetically pleasing and structurally sound designs. |
Definition of a Triangle |
|
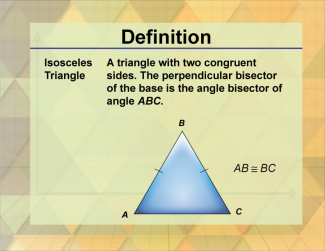
Definition--Triangle Concepts--Isosceles Triangle, Definition 2 |
Isosceles Triangle, Definition 2TopicTriangles DefinitionAn isosceles triangle is a triangle with two sides of equal length and two equal angles opposite those sides. DescriptionAn isosceles triangle is a type of triangle that has two sides of equal length and two equal angles opposite those sides. This symmetry gives the isosceles triangle its unique properties and makes it significant in various geometric constructions. |
Definition of a Triangle |
|
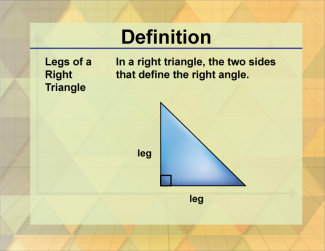
Definition--Triangle Concepts--Legs of a Right Triangle |
Legs of a Right TriangleTopicTriangles DefinitionThe legs of a right triangle are the two sides that form the right angle. DescriptionThe legs of a right triangle are the two sides that form the right angle. These sides are essential in the application of the Pythagorean theorem, which relates the lengths of the legs to the length of the hypotenuse: a2 + b2 = c2 |
Definition of a Triangle |
|
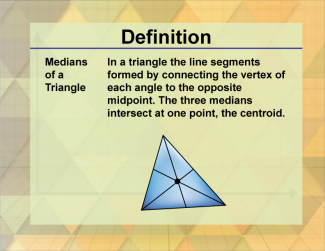
Definition--Triangle Concepts--Medians of a Triangle |
Medians of a TriangleTopicTriangles DefinitionThe medians of a triangle are line segments drawn from each vertex to the midpoint of the opposite side. DescriptionThe medians of a triangle are significant in geometry, representing line segments drawn from each vertex to the midpoint of the opposite side. The point where the medians intersect is called the centroid, which is the triangle's center of mass. |
Definition of a Triangle |
|
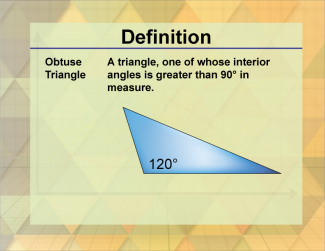
Definition--Triangle Concepts--Obtuse Triangle |
Obtuse TriangleTopicTriangles DefinitionAn obtuse triangle is a triangle with one angle greater than 90 degrees. DescriptionAn obtuse triangle is characterized by having one of its interior angles greater than 90 degrees. This type of triangle is significant in geometry as it represents a unique class of triangles with specific properties. In real-world applications, obtuse triangles are used in various design and architectural projects where specific angle measurements are required. For example, understanding the properties of obtuse triangles helps in creating structures with unique shapes and angles. |
Definition of a Triangle |
|
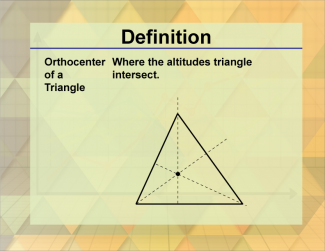
Definition--Triangle Concepts--Orthocenter of a Triangle |
Orthocenter of a TriangleTopicTriangles DefinitionThe orthocenter of a triangle is the point where the three altitudes intersect. DescriptionThe orthocenter of a triangle is a significant point in geometry, representing the intersection of the triangle's three altitudes. Each altitude is a perpendicular line segment drawn from a vertex to the opposite side. This concept is essential in various real-world applications, such as in design and engineering, where precise measurements and symmetry are crucial. For example, understanding the orthocenter helps in creating balanced and structurally sound designs. |
Definition of a Triangle |
|
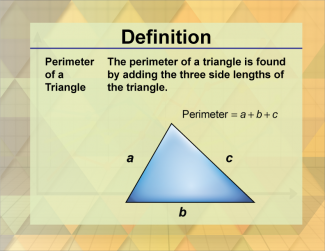
Definition--Triangle Concepts--Perimeter of a Triangle |
Perimeter of a TriangleTopicTriangles DefinitionThe perimeter of a triangle is the sum of the lengths of its three sides. DescriptionThe perimeter of a triangle is a fundamental concept in geometry, representing the total distance around the triangle. The perimeter is calculated by adding the lengths of the triangle's three sides. This concept is essential in various real-world applications, such as in land measurement, construction, and design. For example, calculating the perimeter of a triangular plot of land helps in land valuation and planning. In construction, understanding the perimeter is crucial for determining the amount of materials needed for a project. |
Definition of a Triangle |
|
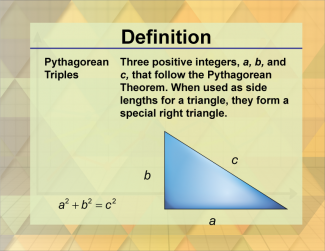
Definition--Triangle Concepts--Pythagorean Triples |
Pythagorean TriplesTopicTriangles DefinitionPythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem: a2 + b2 = c2 DescriptionPythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Common examples include (3, 4, 5) and (5, 12, 13). |
Definition of a Triangle |
|
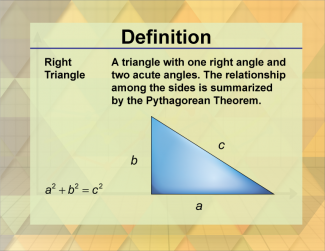
Definition--Triangle Concepts--Right Triangle |
Right TriangleTopicTriangles DefinitionA right triangle is a triangle with one 90-degree angle. DescriptionA right triangle is a type of triangle that has one angle measuring 90 degrees. This type of triangle is fundamental in geometry and trigonometry, as it forms the basis for the Pythagorean theorem: a2 + b2 = c2 This concept is essential in various real-world applications, such as in construction and navigation. For example, right triangles are used to create right angles and ensure accuracy in building projects. They also play a crucial role in various mathematical problems and proofs. |
Definition of a Triangle |
|
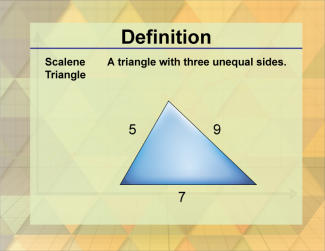
Definition--Triangle Concepts--Scalene Triangle |
Scalene TriangleTopicTriangles DefinitionA scalene triangle is a triangle with all three sides of different lengths and all three angles of different measures. DescriptionA scalene triangle is characterized by having all three sides of different lengths and all three angles of different measures. This type of triangle is significant in geometry as it represents a unique class of triangles with specific properties. |
Definition of a Triangle |
|
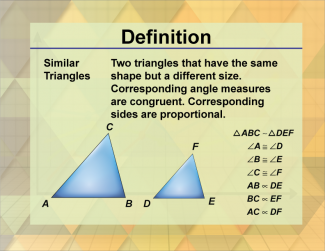
Definition--Triangle Concepts--Similar Triangles |
Similar TrianglesTopicTriangles DefinitionSimilar triangles are triangles that have the same shape but not necessarily the same size, with corresponding angles equal and corresponding sides proportional. DescriptionSimilar triangles are fundamental in geometry, representing triangles that have the same shape but not necessarily the same size. This means that all corresponding angles are equal, and all corresponding sides are proportional. |
Definition of a Triangle |
|
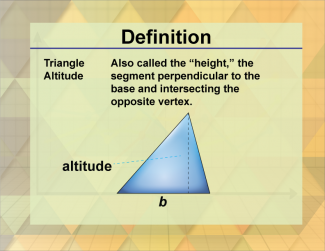
Definition--Triangle Concepts--Triangle Altitude |
Triangle AltitudeTopicTriangles DefinitionThe altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side. DescriptionThe altitude of a triangle is a significant concept in geometry, representing the perpendicular distance from a vertex to the line containing the opposite side. This measurement is crucial in various geometric calculations, such as finding the area of a triangle. |
Definition of a Triangle |
|
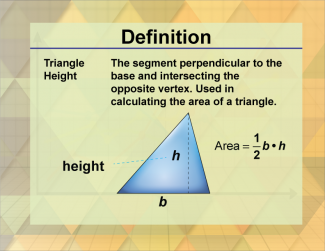
Definition--Triangle Concepts--Triangle Height |
Triangle HeightTopicTriangles DefinitionThe height of a triangle is the perpendicular distance from a vertex to the line containing the opposite side, often used interchangeably with altitude. DescriptionThe height of a triangle, often used interchangeably with altitude, is a crucial concept in geometry. It represents the perpendicular distance from a vertex to the line containing the opposite side. This measurement is essential for calculating the area of a triangle, using the formula: Area= 1/2 × base × height |
Definition of a Triangle |

|
Definition--Triangle Concepts--Triangle Inscribed in a Circle |
Triangle Inscribed in a CircleTopicTriangles DefinitionA triangle inscribed in a circle is a triangle whose vertices all lie on the circumference of the circle. DescriptionA triangle inscribed in a circle, also known as a circumtriangle, is a triangle whose vertices all lie on the circumference of the circle. The circle is called the circumcircle, and its center is the circumcenter of the triangle. |
Definition of a Triangle |
|
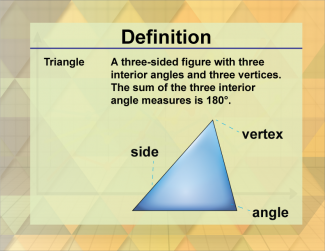
Definition--Triangle Concepts--Triangle, Definition 1 |
Triangle, Definition 1TopicTriangles DefinitionA triangle is a polygon with three edges and three vertices. DescriptionA triangle is one of the simplest and most fundamental shapes in geometry, characterized by having three sides and three vertices. The sum of the interior angles of a triangle is always 180 degrees, which is a key property used in various geometric proofs and constructions. In real-world applications, triangles are used extensively in engineering, architecture, and design due to their inherent stability and strength. For example, triangular structures are often used in bridges and roof trusses to distribute weight evenly and provide support. |
Definition of a Triangle |

|
Definition--Triangle Concepts--Triangle, Definition 2 |
Triangle, Definition 2TopicTriangles DefinitionA triangle is a three-sided polygon with three vertices and three angles. DescriptionA triangle is a three-sided polygon that is fundamental in the study of geometry. Each triangle has three vertices and three angles, and the sum of its interior angles is always 180 degrees. This property is crucial for understanding various geometric principles and solving related problems. |
Definition of a Triangle |
|
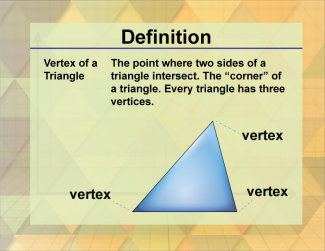
Definition--Triangle Concepts--Vertex of a Triangle |
Vertex of a TriangleTopicTriangles DefinitionA vertex of a triangle is a point where two sides of the triangle meet. DescriptionA vertex of a triangle is one of the three points where the sides of the triangle intersect. Each triangle has three vertices, and these points are crucial for defining the shape and properties of the triangle. |
Definition of a Triangle |

|
Geometry Applications, Triangles, Segment 1, Introduction |
VIDEO: Geometry Applications: Triangles, 1
TopicTriangles DescriptionThis video introduces the importance of triangles in architecture and structural design. It highlights the use of triangles in structures like the Bank of China Tower in Hong Kong, noting their ability to provide strength and stability. The video focuses on the role of triangles in reinforcing skyscrapers to withstand strong winds, especially during typhoon seasons. Key vocabulary includes architectural support, triangular base, and stability. The video sets up a foundation for exploring how triangle properties are applied in real-world contexts. |
Applications of Triangles and Definition of a Triangle |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Constructing an Isosceles Triangle |
In this Slide Show, we show how to construct an isosceles triangle. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: The Perpendicular Bisectors of a Triangle |
In this Slide Show, we show how to construct the perpendicular bisectors of the three sides of a triangle to show they intersect at a single point. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
INSTRUCTIONAL RESOURCE: TI-Nspire App Activity: Constructing an Isosceles Triangle |
In this Slide Show, learn how to use the TI-Nspire App to construct an isosceles triangle. Note: The download is a PPT file. |
Definition of a Triangle and Geometric Constructions with Triangles |
|
Interactive Crossword Puzzle--Triangles |
Interactive Crossword Puzzle--Triangles
This interactive crossword puzzle tests knowledge of key terms on the topic of triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Math Game--Memory Game: Triangles |
Interactive Math Game--Memory Game: Triangles
Use this math game to review triangles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Math Game: Math Riddles--Triangles |
Interactive Math Game: Math Riddles--Triangles
In this Math Riddles Game, have your students review vocabulary around the topic of triangles. The Math Riddles games are useful for practicing: Math Vocabulary, Key Concepts, Critical Thinking. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Word Search Puzzle--Triangles, Puzzle 1 |
Interactive Word Search Puzzle--Triangles, Puzzle 1
Solve an interactive word search puzzle on the topic of Triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Word Search Puzzle--Triangles, Puzzle 2 |
Interactive Word Search Puzzle--Triangles, Puzzle 2
Solve an interactive word search puzzle on the topic of Triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Word Search Puzzle--Triangles, Puzzle 3 |
Interactive Word Search Puzzle--Triangles, Puzzle 3
Solve an interactive word search puzzle on the topic of Triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Word Search Puzzle--Triangles, Puzzle 4 |
Interactive Word Search Puzzle--Triangles, Puzzle 4
Solve an interactive word search puzzle on the topic of Triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Word Search Puzzle--Triangles, Puzzle 5 |
Interactive Word Search Puzzle--Triangles, Puzzle 5
Solve an interactive word search puzzle on the topic of Triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 01 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 01TopicGeometry Basics DescriptionThis math clip art image serves as the title card for a series on classifying triangles by angles. It reads "Classifying Triangles by Angle." This image is part of a comprehensive set designed to teach students about the different types of triangles based on their angles. |
Definition of a Triangle |
|
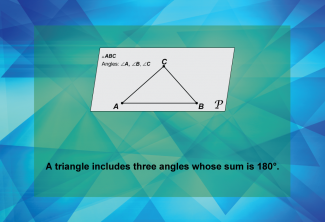
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 02 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 02TopicGeometry Basics DescriptionThis math clip art image is the second in a series about categorizing angles in triangles. It depicts a triangle labeled ABC, illustrating the fundamental principle that a triangle includes three angles whose sum is 180 degrees. This key concept in geometry is visually represented, providing students with a clear understanding of this crucial property of triangles. |
Definition of a Triangle |
|
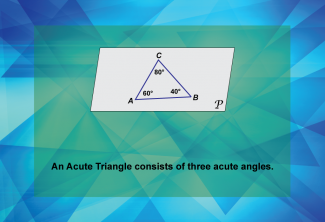
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 03 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 03TopicGeometry Basics DescriptionThis math clip art image is the third in a series about categorizing angles in triangles. It showcases an acute triangle, demonstrating that an acute triangle consists of three acute angles. The image clearly illustrates the defining characteristic of an acute triangle, where all three angles are less than 90 degrees. |
Definition of a Triangle |
|
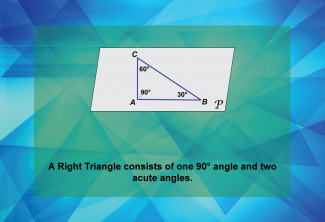
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 04 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 04TopicGeometry Basics DescriptionThis math clip art image is the fourth in a series about categorizing angles in triangles. It presents a right triangle, illustrating that a right triangle consists of one 90-degree angle and two acute angles. The image clearly demonstrates the defining characteristic of a right triangle, emphasizing the 90-degree angle and the two acute angles that complete the 180-degree sum. |
Definition of a Triangle |
|
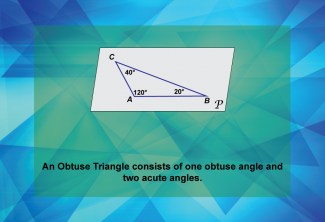
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 05 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 05TopicGeometry Basics DescriptionThis math clip art image is the fifth in a series about categorizing angles in triangles. It showcases an obtuse triangle, demonstrating that an obtuse triangle consists of one obtuse angle and two acute angles. The image clearly illustrates the defining characteristic of an obtuse triangle, highlighting the one angle that is greater than 90 degrees and the two acute angles that complete the 180-degree sum. |
Definition of a Triangle |
|
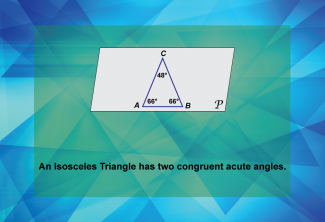
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 06 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 06TopicGeometry Basics DescriptionThis math clip art image is the sixth in a series about categorizing angles in triangles. It depicts an isosceles triangle, illustrating that an isosceles triangle has two congruent acute angles. The image clearly demonstrates the defining characteristic of an isosceles triangle, highlighting the two equal angles and their corresponding equal sides. |
Definition of a Triangle |
|
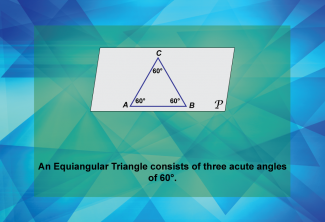
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 07 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 07TopicGeometry Basics DescriptionThis math clip art image is the seventh in a series about categorizing angles in triangles. It showcases an equiangular triangle, demonstrating that an equiangular triangle consists of three acute angles of 60 degrees each. The image clearly illustrates the defining characteristic of an equiangular triangle, highlighting that all three angles are equal and measure 60 degrees. |
Definition of a Triangle |
|
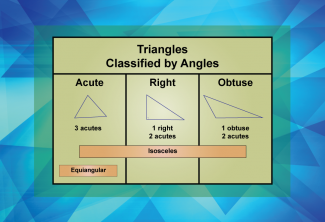
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 08 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 08TopicGeometry Basics DescriptionThis math clip art image is the eighth in a series about categorizing angles in triangles. It presents a comprehensive table that summarizes the three categories of triangles. The image provides a clear overview of the different types of triangles classified by their angles, including acute, right, and obtuse triangles, along with their defining characteristics. |
Definition of a Triangle |

|
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 09 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 09TopicGeometry Basics DescriptionThis math clip art image, which is the ninth in the series about categorizing triangles by angles, showcases real-world examples of acute triangles. It features a Yield sign and a No Passing Zone sign, both of which are shaped like acute triangles. These examples illustrate how acute triangles, which consist of three angles that are all less than 90 degrees, can be found in everyday objects. The sharp angles of these signs not only serve a functional purpose in guiding drivers but also provide a clear visual representation of acute triangles in a real-world context. |
Definition of a Triangle |

|
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 10 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 10TopicGeometry Basics DescriptionThis math clip art image is the tenth in the series about categorizing triangles by angles, depicting a real-world example of a right triangle. It shows the right triangle portion of a truss, which effectively illustrates the structural applications of right triangles in engineering and construction. Right triangles consist of one 90-degree angle and two acute angles, collaborating harmoniously to provide strength and stability in various designs. |
Definition of a Triangle |
|
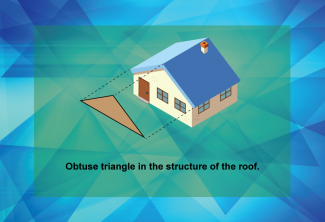
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 11 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 11TopicGeometry Basics DescriptionThis math clip art image, which is the eleventh in the series about categorizing triangles by angles, illustrates a real-world example of an obtuse triangle. It depicts the roof of a house, showcasing the triangular shape it forms, where one angle is greater than 90 degrees, categorizing it as an obtuse triangle. This example emphasizes the significance of obtuse triangles in architecture and design, highlighting how these shapes provide aesthetic and structural benefits. |
Definition of a Triangle |
|
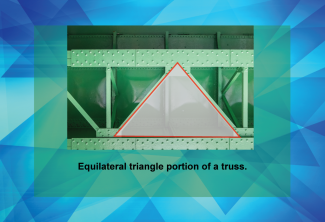
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 12 |
Math Clip Art--Geometry Basics--Classifying Triangles by Angles 12TopicGeometry Basics DescriptionThis math clip art image is the twelfth in the series about categorizing triangles by angles, depicting a real-world example of an equilateral triangle. It shows a portion of a truss, illustrating how equilateral triangles, which have all three angles equal to 60 degrees, are utilized in construction for their symmetrical properties. This example underscores the significance of equilateral triangles in design, providing both aesthetic appeal and structural integrity. |
Definition of a Triangle |

|
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 01 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 01TopicGeometry Basics DescriptionThis image is part of a series about categorizing triangles, serving as a title card for the collection. It introduces the concept of "Classifying Triangles by Side," setting the stage for a comprehensive exploration of triangle types. The use of clear, visually appealing math clip art is crucial in geometry education, as it helps students visualize abstract concepts and makes learning more engaging. |
Definition of a Triangle |
|
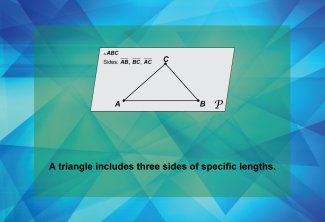
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 02 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 02TopicGeometry Basics DescriptionThis image illustrates a fundamental concept in triangle geometry: every triangle consists of three sides, each with its own specific length. It's an essential starting point for understanding how triangles can be classified based on their sides. Math clip art like this is invaluable in geometry education as it provides a clear, visual representation of abstract concepts. Teachers can use this image to introduce the basic definition of a triangle and as a foundation for more complex classifications. |
Definition of a Triangle |
|
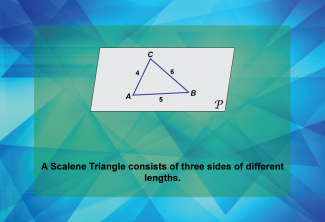
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 03 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 03TopicGeometry Basics DescriptionThis image introduces the concept of a scalene triangle, which is characterized by having three sides of different lengths. It's an important classification in triangle geometry and helps students understand the diversity of triangle types. Using math clip art in this context allows for clear visual representation of the unique property of scalene triangles. Teachers can use this image to help students identify and understand this specific triangle classification. |
Definition of a Triangle |
|
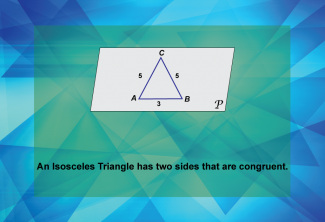
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 04 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 04TopicGeometry Basics DescriptionThis image introduces the concept of an isosceles triangle, which is defined by having two sides that are congruent or equal in length. It's a key classification in triangle geometry and helps students understand another important type of triangle. Math clip art like this is crucial in geometry education as it provides a clear visual representation of the unique property of isosceles triangles. Teachers can use this image to help students identify and understand this specific triangle classification. |
Definition of a Triangle |
|
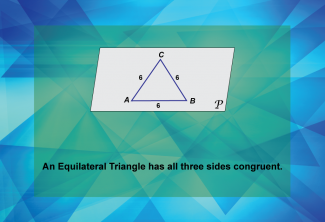
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 05 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 05TopicGeometry Basics DescriptionThis image introduces the concept of an equilateral triangle, which is characterized by having all three sides congruent or equal in length. It's a significant classification in triangle geometry and represents a special case of triangle symmetry. Using math clip art in this context allows for a clear visual representation of the unique property of equilateral triangles. Teachers can use this image to help students identify and understand this specific triangle classification and its implications for angle measures. |
Definition of a Triangle |
|
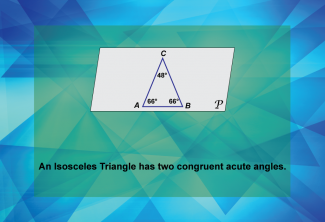
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 06 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 06TopicGeometry Basics DescriptionThis image expands on the concept of isosceles triangles by highlighting an important property: an isosceles triangle has two congruent acute angles. This information helps students understand the relationship between side lengths and angles in triangles. Math clip art like this is invaluable in geometry education as it visually demonstrates the connection between a triangle's sides and its angles. Teachers can use this image to deepen students' understanding of isosceles triangles and introduce the concept of angle-side relationships in triangles. |
Definition of a Triangle |
|
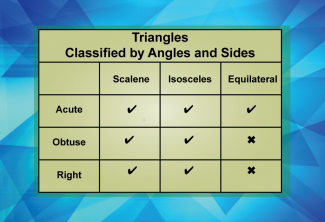
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 07 |
Math Clip Art--Geometry Basics--Classifying Triangles by Sides 07TopicGeometry Basics DescriptionThis image presents a table that explores various combinations of triangle classifications. It helps students understand how different triangle types can be related and combined, deepening their comprehension of triangle geometry. Using math clip art in this tabular format is particularly effective for organizing and comparing different triangle classifications. Teachers can use this image to guide students through the various combinations and discuss the relationships between different triangle types. |
Definition of a Triangle |