Illustrative Math Alignment: Grade 6 Unit 2
Introducing Ratios
Lesson 14: Solving Equivalent Ratio Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Clip Art--Ratios, Proportions, Percents--Rates 07 |
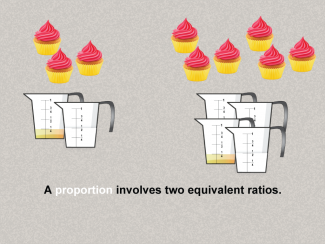
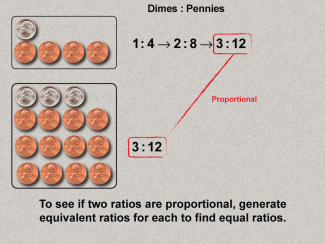
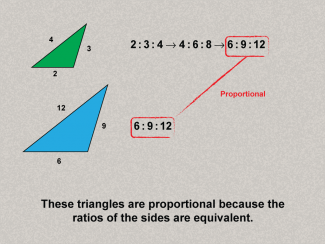
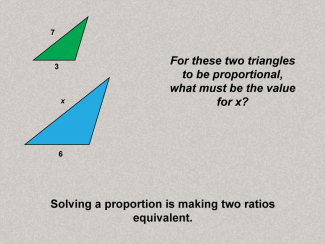
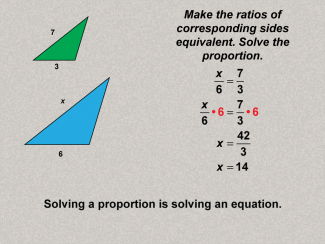
Math Clip Art--Ratios, Proportions, Percents--Rates 07
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Rates 08 |
Math Clip Art--Ratios, Proportions, Percents--Rates 08
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Rates 09 |
Math Clip Art--Ratios, Proportions, Percents--Rates 09
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Rates 10 |
Math Clip Art--Ratios, Proportions, Percents--Rates 10
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 01 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 02 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 03 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 04 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 05 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 06 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 07 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 07
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 08 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 08
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 09 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 09
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 10 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 10
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Ratios 11 |
Math Clip Art--Ratios, Proportions, Percents--Ratios 11
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Ratios and Rates |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
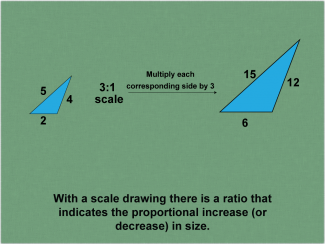
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
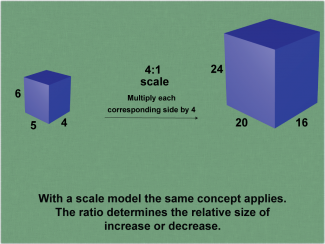
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
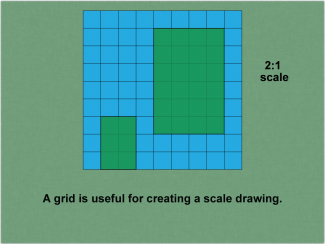
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 |
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 3 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 3
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 30 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 30
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 31 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 31
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 32 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 32
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 33 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 33
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 34 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 34
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 35 |
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 35
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
