IXL Ad

Illustrative Math-Media4Math Alignment

 

 

Illustrative Math Alignment: Grade 6 Unit 3

Unit Rates and Percentages

Lesson 12: Percentages and Tape Diagrams

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image Title Body Curriculum Nodes
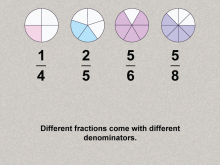
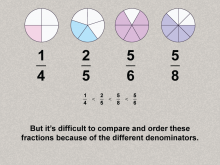
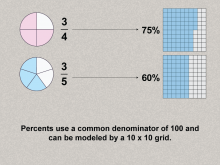
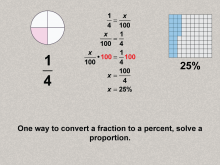
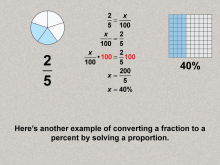
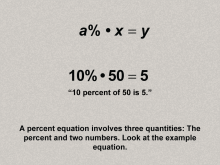
Math Clip Art--Ratios, Proportions, Percents--Intro to Percents, Image 11 Math Clip Art--Ratios, Proportions, Percents--Percents 11 Math Clip Art--Ratios, Proportions, Percents--Percents 11

This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents.

 Percents
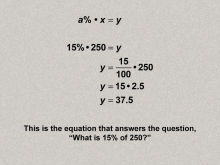
Math Clip Art--Ratios, Proportions, Percents--Intro to Percents, Image 12 Math Clip Art--Ratios, Proportions, Percents--Percents 12 Math Clip Art--Ratios, Proportions, Percents--Percents 12

This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents.

 Percents
Math Clip Art--Ratios, Proportions, Percents--Intro to Percents, Image 13 Math Clip Art--Ratios, Proportions, Percents--Percents 13 Math Clip Art--Ratios, Proportions, Percents--Percents 13

This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents.

 Percents
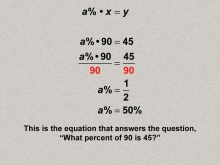
Math Clip Art--Ratios, Proportions, Percents--Intro to Percents, Image 14 Math Clip Art--Ratios, Proportions, Percents--Percents 14 Math Clip Art--Ratios, Proportions, Percents--Percents 14

This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents.

 Percents
Math Clip Art--Ratios, Proportions, Percents--Intro to Percents, Image 15 Math Clip Art--Ratios, Proportions, Percents--Percents 15 Math Clip Art--Ratios, Proportions, Percents--Percents 15

This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents.

 Percents
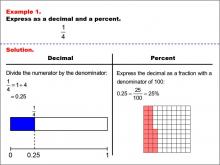
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1

Topic

Fractions

 Relate Fractions to Decimals
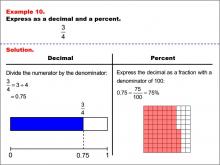
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 10 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 10 Fractions, Decimals, and Percents: Example 10

Topic

Fractions

 Relate Fractions to Decimals
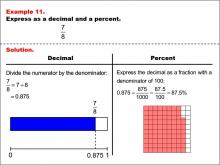
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 11 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 11 Fractions, Decimals, and Percents: Example 11

Topic

Fractions

 Relate Fractions to Decimals
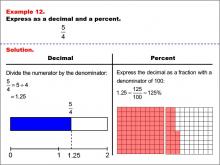
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 12 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 12 Fractions, Decimals, and Percents: Example 12

Topic

Fractions

 Relate Fractions to Decimals
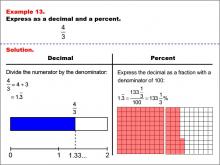
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 13 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 13 Fractions, Decimals, and Percents: Example 13

Topic

Fractions

 Relate Fractions to Decimals
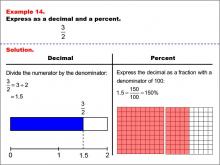
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 14 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 14 Fractions, Decimals, and Percents: Example 14

Topic

Fractions

 Relate Fractions to Decimals
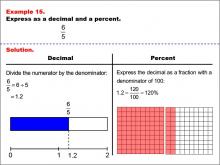
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 15 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 15 Fractions, Decimals, and Percents: Example 15

Topic

Fractions

 Relate Fractions to Decimals
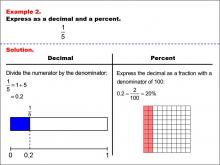
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 2 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 2 Fractions, Decimals, and Percents: Example 2

Topic

Fractions

 Relate Fractions to Decimals
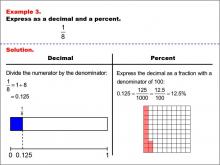
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 3 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 3 Fractions, Decimals, and Percents: Example 3

Topic

Fractions

 Relate Fractions to Decimals
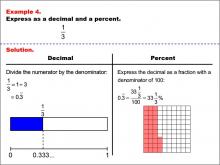
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 4 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 4 Fractions, Decimals, and Percents: Example 4

Topic

Fractions

 Relate Fractions to Decimals
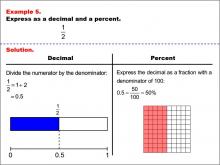
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 5 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 5 Fractions, Decimals, and Percents: Example 5

Topic

Fractions

 Relate Fractions to Decimals
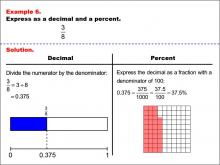
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 6 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 6 Fractions, Decimals, and Percents: Example 6

Topic

Fractions

 Relate Fractions to Decimals
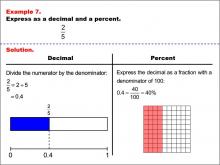
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 7 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 7 Fractions, Decimals, and Percents: Example 7

Topic

Fractions

 Relate Fractions to Decimals
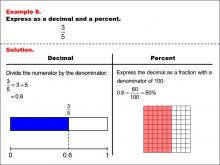
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 8 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 8 Fractions, Decimals, and Percents: Example 8

Topic

Fractions

 Relate Fractions to Decimals
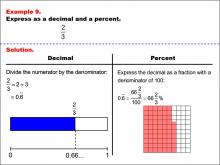
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 9 Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 9 Fractions, Decimals, and Percents: Example 9

Topic

Fractions

 Relate Fractions to Decimals
Math Example--Math of Money--Calculating Tax--Example 1 Math Example--Math of Money--Calculating Tax--Example 1 Math Example--Math of Money--Calculating Tax--Example 1

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 10 Math Example--Math of Money--Calculating Tax--Example 10 Math Example--Math of Money--Calculating Tax--Example 10

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 2 Math Example--Math of Money--Calculating Tax--Example 2 Math Example--Math of Money--Calculating Tax--Example 2

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 3 Math Example--Math of Money--Calculating Tax--Example 3 Math Example--Math of Money--Calculating Tax--Example 3

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 4 Math Example--Math of Money--Calculating Tax--Example 4 Math Example--Math of Money--Calculating Tax--Example 4

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 5 Math Example--Math of Money--Calculating Tax--Example 5 Math Example--Math of Money--Calculating Tax--Example 5

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 6 Math Example--Math of Money--Calculating Tax--Example 6 Math Example--Math of Money--Calculating Tax--Example 6

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 7 Math Example--Math of Money--Calculating Tax--Example 7 Math Example--Math of Money--Calculating Tax--Example 7

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 8 Math Example--Math of Money--Calculating Tax--Example 8 Math Example--Math of Money--Calculating Tax--Example 8

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tax--Example 9 Math Example--Math of Money--Calculating Tax--Example 9 Math Example--Math of Money--Calculating Tax--Example 9

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 1 Math Example--Math of Money--Calculating Tips and Commissions--Example 1 Math Example--Math of Money--Calculating Tips and Commissions--Example 1

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 10 Math Example--Math of Money--Calculating Tips and Commissions--Example 10 Math Example--Math of Money--Calculating Tips and Commissions--Example 10

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 2 Math Example--Math of Money--Calculating Tips and Commissions--Example 2 Math Example--Math of Money--Calculating Tips and Commissions--Example 2

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 3 Math Example--Math of Money--Calculating Tips and Commissions--Example 3 Math Example--Math of Money--Calculating Tips and Commissions--Example 3

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 4 Math Example--Math of Money--Calculating Tips and Commissions--Example 4 Math Example--Math of Money--Calculating Tips and Commissions--Example 4

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 5 Math Example--Math of Money--Calculating Tips and Commissions--Example 5 Math Example--Math of Money--Calculating Tips and Commissions--Example 5

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 6 Math Example--Math of Money--Calculating Tips and Commissions--Example 6 Math Example--Math of Money--Calculating Tips and Commissions--Example 6

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 7 Math Example--Math of Money--Calculating Tips and Commissions--Example 7 Math Example--Math of Money--Calculating Tips and Commissions--Example 7

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 8 Math Example--Math of Money--Calculating Tips and Commissions--Example 8 Math Example--Math of Money--Calculating Tips and Commissions--Example 8

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 9 Math Example--Math of Money--Calculating Tips and Commissions--Example 9 Math Example--Math of Money--Calculating Tips and Commissions--Example 9

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 1 Math Example--Math of Money--Simple Interest--Example 1 Math Example--Math of Money--Simple Interest--Example 1

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 10 Math Example--Math of Money--Simple Interest--Example 10 Math Example--Math of Money--Simple Interest--Example 10

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 2 Math Example--Math of Money--Simple Interest--Example 2 Math Example--Math of Money--Simple Interest--Example 2

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 3 Math Example--Math of Money--Simple Interest--Example 3 Math Example--Math of Money--Simple Interest--Example 3

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 4 Math Example--Math of Money--Simple Interest--Example 4 Math Example--Math of Money--Simple Interest--Example 4

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 5 Math Example--Math of Money--Simple Interest--Example 5 Math Example--Math of Money--Simple Interest--Example 5

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 6 Math Example--Math of Money--Simple Interest--Example 6 Math Example--Math of Money--Simple Interest--Example 6

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 7 Math Example--Math of Money--Simple Interest--Example 7 Math Example--Math of Money--Simple Interest--Example 7

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 8 Math Example--Math of Money--Simple Interest--Example 8 Math Example--Math of Money--Simple Interest--Example 8

This is part of a collection of math examples that focus on money.

 Percents
Math Example--Math of Money--Simple Interest--Example 9 Math Example--Math of Money--Simple Interest--Example 9 Math Example--Math of Money--Simple Interest--Example 9

This is part of a collection of math examples that focus on money.

 Percents