
Illustrative Math Alignment: Grade 6 Unit 3
Unit Rates and Percentages
Lesson 14: Solving Percentage Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
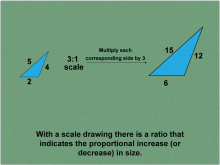
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
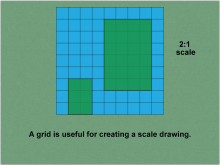
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
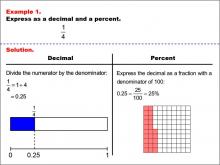
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1 | Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 1TopicFractions |
Relate Fractions to Decimals |
|
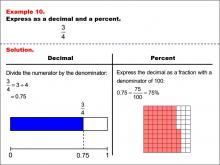
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 10 | Fractions, Decimals, and Percents: Example 10TopicFractions |
Relate Fractions to Decimals |
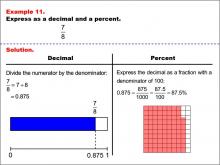
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 11 | Fractions, Decimals, and Percents: Example 11TopicFractions |
Relate Fractions to Decimals |
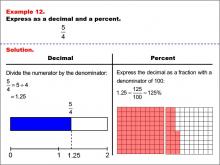
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 12 | Fractions, Decimals, and Percents: Example 12TopicFractions |
Relate Fractions to Decimals |
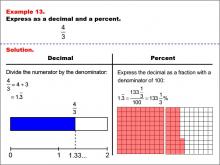
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 13 | Fractions, Decimals, and Percents: Example 13TopicFractions |
Relate Fractions to Decimals |
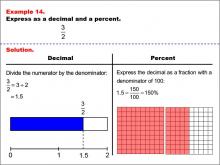
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 14 | Fractions, Decimals, and Percents: Example 14TopicFractions |
Relate Fractions to Decimals |
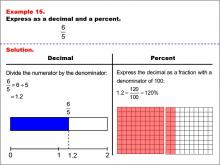
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 15 | Fractions, Decimals, and Percents: Example 15TopicFractions |
Relate Fractions to Decimals |
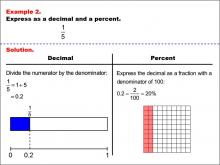
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 2 | Fractions, Decimals, and Percents: Example 2TopicFractions |
Relate Fractions to Decimals |
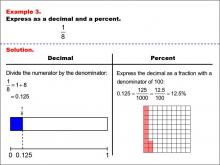
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 3 | Fractions, Decimals, and Percents: Example 3TopicFractions |
Relate Fractions to Decimals |
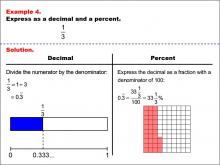
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 4 | Fractions, Decimals, and Percents: Example 4TopicFractions |
Relate Fractions to Decimals |
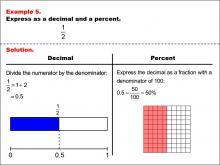
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 5 | Fractions, Decimals, and Percents: Example 5TopicFractions |
Relate Fractions to Decimals |
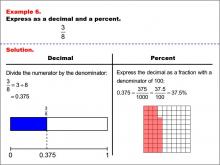
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 6 | Fractions, Decimals, and Percents: Example 6TopicFractions |
Relate Fractions to Decimals |
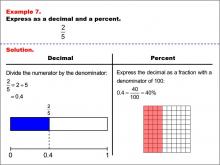
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 7 | Fractions, Decimals, and Percents: Example 7TopicFractions |
Relate Fractions to Decimals |
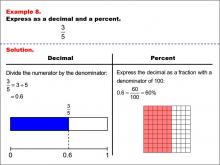
|
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 8 | Fractions, Decimals, and Percents: Example 8TopicFractions |
Relate Fractions to Decimals |
|
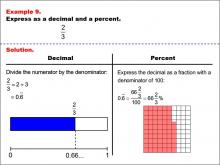
Math Example--Fraction Properties--Fractions, Decimals, and Percents: Example 9 | Fractions, Decimals, and Percents: Example 9TopicFractions |
Relate Fractions to Decimals |

|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 6 | Math Example--Math of Money--Calculating Tax--Example 6TopicThe Math of Money DescriptionWhat is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 7 | Math Example--Math of Money--Calculating Tax--Example 7TopicThe Math of Money DescriptionWhat is the tax due on a $1399 purchase when the sales tax rate is 7.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 8 | Math Example--Math of Money--Calculating Tax--Example 8TopicThe Math of Money DescriptionWhat is the tax due on a $1575.50 purchase when the sales tax rate is 8.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tax--Example 9 | Math Example--Math of Money--Calculating Tax--Example 9TopicThe Math of Money DescriptionWhat is the tax due on a $1999.99 purchase when the sales tax rate is 9.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 1 | Math Example--Math of Money--Calculating Tips and Commissions--Example 1TopicThe Math of Money DescriptionCalculate a 15% tip on a $50 restaurant bill. The problem requires finding 15% of 50. To calculate the tip, multiply the cost (50) by the tip rate (0.15). Tip = 50 * 0.15 = 7.50. The answer is $7.50. In general, the topic 'The Math of Money' covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 10 | Math Example--Math of Money--Calculating Tips and Commissions--Example 10TopicThe Math of Money DescriptionCalculate a 9.5% sales commission on a $350,999 sale. The problem requires finding 9.5% of 350,999. To calculate the commission, multiply the sale amount (350,999) by the commission rate (0.095). Commission = 350,999 * 0.095 ≈ 33,344.91. The answer is approximately $33,344.91. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 2 | Math Example--Math of Money--Calculating Tips and Commissions--Example 2TopicThe Math of Money DescriptionCalculate a 16% tip on a $55 restaurant bill. The problem requires finding 16% of 55. To calculate the tip, multiply the cost (55) by the tip rate (0.16). Tip = 55 * 0.16 = 8.8. The answer is $8.80. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 3 | Math Example--Math of Money--Calculating Tips and Commissions--Example 3TopicThe Math of Money DescriptionCalculate an 18% tip on a $75.50 restaurant bill. The problem requires finding 18% of 75.50. To calculate the tip, multiply the cost (75.50) by the tip rate (0.18). Tip = 75.50 * 0.18 = 13.59. The answer is $13.59. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 4 | Math Example--Math of Money--Calculating Tips and Commissions--Example 4TopicThe Math of Money DescriptionCalculate a 19.5% tip on a $49.99 restaurant bill. The problem requires finding 19.5% of 49.99. To calculate the tip, multiply the cost (49.99) by the tip rate (0.195). Tip = 49.99 * 0.195 Å 9.75. The answer is approximately $9.75. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 5 | Math Example--Math of Money--Calculating Tips and Commissions--Example 5TopicThe Math of Money DescriptionCalculate a 22.5% tip on a $159.99 restaurant bill. The problem requires finding 22.5% of 159.99. To calculate the tip, multiply the cost (159.99) by the tip rate (0.225). Tip = 159.99 * 0.225 ≈ 35.99. The answer is approximately $35.99. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 6 | Math Example--Math of Money--Calculating Tips and Commissions--Example 6TopicThe Math of Money DescriptionCalculate a 5% sales commission on a $1000 sale. The problem requires finding 5% of 1000. To calculate the commission, multiply the sale amount (1000) by the commission rate (0.05). Commission = 1000 * 0.05 = 50. The answer is $50. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 7 | Math Example--Math of Money--Calculating Tips and Commissions--Example 7TopicThe Math of Money DescriptionCalculate a 6% sales commission on a $1200 sale. The problem requires finding 6% of 1200. To calculate the commission, multiply the sale amount (1200) by the commission rate (0.06). Commission = 1200 * 0.06 = 72. The answer is $72. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 8 | Math Example--Math of Money--Calculating Tips and Commissions--Example 8TopicThe Math of Money DescriptionCalculate a 7.5% sales commission on a $25,500 sale. The problem requires finding 7.5% of 25,500. To calculate the commission, multiply the sale amount (25,500) by the commission rate (0.075). Commission = 25,500 * 0.075 = 1912.50. The answer is $1,912.50. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |

|
Math Example--Math of Money--Calculating Tips and Commissions--Example 9 | Math Example--Math of Money--Calculating Tips and Commissions--Example 9TopicThe Math of Money DescriptionCalculate an 8.5% sales commission on a $125,500 sale. The problem requires finding 8.5% of 125,500. To calculate the commission, multiply the sale amount (125,500) by the commission rate (0.085). Commission = 125,500 * 0.085 = 10,667.50. The answer is $10,667.50. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 1 | Math Example--Math of Money--Simple Interest--Example 1TopicThe Math of Money DescriptionAn investment of $1000 earns 10% interest. Calculate the total amount of the investment after applying simple interest. The solution uses the formula for simple interest: Total Amount = P * (1 + r). Substitute P = 1000 and r = 0.1 to get 1000 * (1 + 0.1) = 1000 * 1.1 = 1100. Thus, the total amount is $1100. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 10 | Math Example--Math of Money--Simple Interest--Example 10TopicThe Math of Money DescriptionAn investment of $50,999 earns 21.55% interest. Calculate the total amount of the investment after applying simple interest. Substitute P = 50999 and r = 0.2155 in the formula Total Amount = P * (1 + r) to get 50999 * (1 + 0.2155) = 50999 * 1.2155 ≈ 61,989.28. Thus, the total amount is approximately $61,989.28. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 2 | Math Example--Math of Money--Simple Interest--Example 2TopicThe Math of Money DescriptionAn investment of $5000 earns 5% interest. Calculate the total amount of the investment after applying simple interest. Using the formula Total Amount = P * (1 + r), substitute P = 5000 and r = 0.05. This gives 5000 * (1 + 0.05) = 5000 * 1.05 = 5250. Therefore, the total amount is $5250. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 3 | Math Example--Math of Money--Simple Interest--Example 3TopicThe Math of Money DescriptionAn investment of $10,500 earns 12% interest. Calculate the total amount of the investment after applying simple interest. Apply the formula Total Amount = P * (1 + r). With P = 10500 and r = 0.12, calculate 10500 * (1 + 0.12) = 10500 * 1.12 = 11760. So, the total amount is $11760. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 4 | Math Example--Math of Money--Simple Interest--Example 4TopicThe Math of Money DescriptionAn investment of $999 earns 15% interest. Calculate the total amount of the investment after applying simple interest. Substitute P = 999 and r = 0.15 into the formula Total Amount = P * (1 + r), resulting in 999 * (1 + 0.15) = 999 * 1.15 = 1148.85. Therefore, the total amount is $1148.85. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 5 | Math Example--Math of Money--Simple Interest--Example 5TopicThe Math of Money DescriptionAn investment of $99.99 earns 7% interest. Calculate the total amount of the investment after applying simple interest. Using the formula Total Amount = P * (1 + r) with P = 99.99 and r = 0.07, compute 99.99 * (1 + 0.07) = 99.99 * 1.07 ≅ 106.99. The total amount is approximately $106.99. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 6 | Math Example--Math of Money--Simple Interest--Example 6TopicThe Math of Money DescriptionAn investment of $20,000 earns 5.5% interest. Calculate the total amount of the investment after applying simple interest. With P = 20000 and r = 0.055, use the formula Total Amount = P * (1 + r) to get 20000 * (1 + 0.055) = 20000 * 1.055 = 21,100. Therefore, the total amount is $21,100. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 7 | Math Example--Math of Money--Simple Interest--Example 7TopicThe Math of Money DescriptionAn investment of $25,550 earns 10.75% interest. Calculate the total amount of the investment after applying simple interest. Substitute P = 25550 and r = 0.1075 in Total Amount = P * (1 + r). This gives 25550 * (1 + 0.1075) = 25550 * 1.1075 = 26,955.25. So, the total amount is $26,955.25. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |

|
Math Example--Math of Money--Simple Interest--Example 8 | Math Example--Math of Money--Simple Interest--Example 8TopicThe Math of Money DescriptionAn investment of $999.99 earns 7.5% interest. Calculate the total amount of the investment after applying simple interest. Using P = 999.99 and r = 0.075 in Total Amount = P * (1 + r), calculate 999.99 * (1 + 0.075) = 999.99 * 1.075 = 1074.99. Thus, the total amount is approximately $1074.99. Understanding the math of money concepts is crucial for students, as it forms the basis for financial literacy. Examples like this showcase the practical application of simple interest formulas, helping learners to connect theoretical knowledge with real-world scenarios. |
Percents |