Illustrative Math Alignment: Grade 6 Unit 3

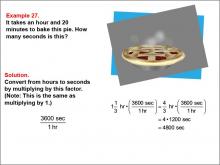
Topic

Ratios and Rates

Description

This example explores time unit conversion, specifically converting hours and minutes to seconds in the context of baking a pie. The image shows a steaming pie, providing a real-world scenario for the mathematical problem.

Understanding time unit conversions, especially when dealing with mixed units, is important in various fields such as cooking, manufacturing, and project management. This example demonstrates how to use conversion factors to change units, illustrating the practical application of multiplication in time-related scenarios.

Topic

Ratios and Rates

Description

This example focuses on time unit conversion in a sports context, specifically converting minutes and seconds to seconds for a horse race lap time. The image shows a horse, providing a visual context for the mathematical problem.

Understanding time unit conversions is crucial in many sports, especially those involving racing and timed events. This example demonstrates how to use conversion factors to change units and add different time units, illustrating the practical application of multiplication and addition in sports-related time scenarios.

Topic

Ratios and Rates

Description

This example explores time unit conversion in an IT context, specifically converting seconds to minutes for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem.

Understanding time unit conversions is crucial in many technological fields, especially in IT and user experience analysis. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division in time-related measurement scenarios. It also introduces the concept of mixed numbers in the result.

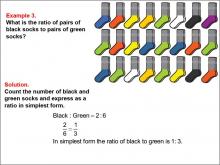
Topic

Ratios and Rates

Description

This example focuses on ratios using black and green socks. The image displays a collection of socks, and students are tasked with determining the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 6 pairs of green socks, resulting in a ratio of 2 : 6, which simplifies to 1 : 3.

Topic

Ratios and Rates

Description

This example focuses on time unit conversion in an IT context, specifically converting seconds to hours for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem.

Topic

Ratios and Rates

Description

This example focuses on temperature unit conversion, specifically converting Celsius to Fahrenheit for the boiling point of water. The image shows a beaker of boiling water, providing a visual context for the mathematical problem.

Understanding temperature unit conversions is crucial in many scientific fields, including chemistry, physics, and meteorology. This example demonstrates how to use a conversion formula to change units, illustrating the practical application of mathematical equations in real-world temperature scenarios.

Topic

Ratios and Rates

Description

This example explores temperature unit conversion, specifically converting Fahrenheit to Celsius for the freezing point of water. The image shows icicles, providing a visual representation of the freezing temperature for the mathematical problem.

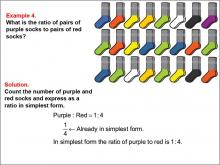
Topic

Ratios and Rates

Description

This example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form.

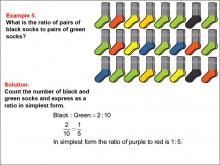
Topic

Ratios and Rates

Description

This example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5.

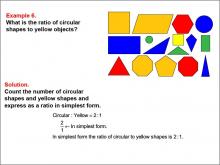
Topic

Ratios and Rates

Description

This example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form.

Topic

Ratios and Rates

Description

This example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3.

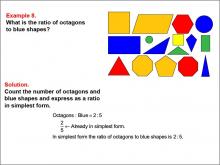
Topic

Ratios and Rates

Description

This example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form.

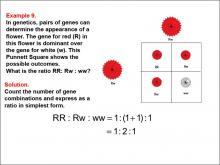
Topic

Ratios and Rates

Description

This example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle.

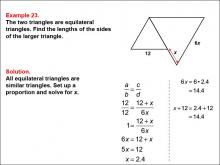
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units.

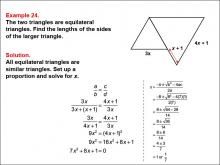
Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with algebraic expressions. Two rectangles are shown, with the smaller one having sides of 5 and 12, and the larger one having sides of x + 5 and 3x + 6. The problem requires setting up a proportion: 5 / 12 = (x + 5) / (3x + 6). Solving this equation leads to x = 10, which then allows us to find the side lengths of the larger rectangle as 15 and 36.

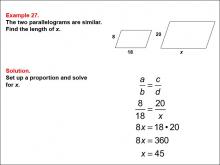
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms. Two parallelograms are shown, with the smaller one having sides of 8 and 18, and the larger one having sides of 20 and x. The problem requires finding the length of side x by setting up a proportion: 8 / 18 = 20 / x. Solving this equation leads to x = 45.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, with the smaller one having sides of 9 and 21, and the larger one having sides of x + 12 and 4x + 3. The problem requires setting up a proportion: 9 / 21 = (x + 12) / (4x + 3). Solving this equation leads to x = 15, which then allows us to find the side lengths of the larger parallelogram as 27 and 63.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two triangles are similar using proportions. Two triangles are shown, both with a 70° angle. The first triangle has sides of 12 and 10, while the second has sides of 18 and 15. The problem requires setting up a proportion to check for similarity: 12 / 10 = 18 / 15. After simplifying, both ratios are equal (6 / 5 = 6 / 5), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for b in a proportion where a = 8, c = 4, and d = 3. We set up the proportion 8 / b = 4 / 3 and solve for b, resulting in b = 6. This problem shows how to find an unknown value in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two triangles are not similar using proportions. Two triangles are shown, both with a 75° angle. The first triangle has sides of 15 and 9, while the second has sides of 28 and 18. The problem requires setting up a proportion to check for similarity: 15 / 9 = 28 / 18. After simplifying, the ratios are not equal (5 / 3 ≠ 14 / 9), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two right triangles are similar using proportions. Two right triangles are shown, one with legs of length 4 and 3, and the other with legs of length 10 and 7.5. The problem requires setting up a proportion to check for similarity: 4 / 3 = 10 / 7.5. After simplifying, both ratios are equal (4 / 3 = 4 / 3), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two right triangles are not similar using proportions. Two right triangles are shown, one with legs of length 12 and 5, and the other with legs of length 35 and 15. The problem requires setting up a proportion to check for similarity: 12 / 5 = 35 / 15. After simplifying, the ratios are not equal (12 / 5 ≠ 7 / 3), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two rectangles are similar using proportions. Two rectangles are shown, with the first having dimensions 3 and 8, and the second having dimensions 9 and 24. The problem requires setting up a proportion to check for similarity: 3 / 8 = 9 / 24. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two rectangles are similar using proportions with algebraic expressions. Two rectangles are shown, with the first having dimensions 11.5 and 23, and the second having dimensions 23x and 46x. The problem requires setting up a proportion to check for similarity: 11.5 / 23 = 23x / 46x. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar for any value of x.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are similar using proportions. Two parallelograms are shown, with the first having dimensions 6 and 9, and the second having dimensions 15 and 22.5. The problem requires setting up a proportion to check for similarity: 6 / 9 = 15 / 22.5. After simplifying, the ratios are equal, confirming that the parallelograms are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are not similar using proportions. Two parallelograms are shown, with the first having dimensions 9 and 28, and the second having dimensions 18 and 54. The problem requires setting up a proportion to check for similarity: 9 / 18 ≠ 28 / 54. After simplifying, the ratios are not equal, concluding that the parallelograms are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with side lengths 9 and 18, and the other with expressions 6x and 10x + 6. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 9 / 18 = 6x / (10x + 6). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with side lengths 4 and 3, and the other with expressions 3x and 2x + 1. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 4 / 3 = 3x / (2x + 1). Solving this equation leads to x = 4.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with an unknown side length. Two rectangles are shown, one with side lengths of 4 and x, and the other with side lengths of 15 and 4. The problem requires setting up a proportion to determine the value of x for which the rectangles are similar: 4 / 15 = x / 4. Solving this equation leads to x = 16/15.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for b in a proportion where a is expressed as x + 2, and c and d are given constants (c = 5, d = 2). We set up the equation (x + 2) / b = 5 / 2 and solve for b, resulting in the expression b = (2(x + 2)) / 5. This problem demonstrates how to handle algebraic expressions in proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, one with side lengths of 6 and x, and the other with expressions of 3x + 2 and 22. The problem requires setting up a proportion to determine the value of x for which the parallelograms are similar: 6 / 22 = x / (3x + 2). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for c in a proportion where a = 9, b = 4, and d = 12. We set up the proportion 9 / 4 = c / 12 and solve for c, resulting in c = 27. This problem shows how to find an unknown value in the numerator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for c in a proportion where a = 8, b = 3, and d is expressed as x + 3. We set up the equation 8 / 3 = c / (x + 3) and solve for c, resulting in the expression c = (8(x + 3)) / 3. This problem demonstrates how to handle algebraic expressions in the denominator of a proportion.