
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 16: Solving Problems Involving Fractions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Video Definition 7--Fraction Concepts--Fraction | Video Definition 7--Fraction Concepts--Fraction
TopicFractions DescriptionFraction: A number representing part of a whole, usually written as the ratio of a numerator and a non-zero denominator. Examples include 4/16, 3/4, and 7/4, with visuals explaining numerator and denominator. This foundational term establishes the basic structure and meaning of fractions, essential for all subsequent fraction concepts. |
Fractions and Mixed Numbers |

|
Video Definition 6--Fraction Concepts--Equivalent Fraction | Video Definition 6--Fraction Concepts--Equivalent Fraction
TopicFractions DescriptionEquivalent Fraction: A fraction with the same numerical value as another fraction, but whose numerator and denominator are multiplied by a common factor. Examples show 1/2 = 2/4 and 2/3 = 6/9. This term illustrates how fractions can be rewritten to have different forms while maintaining equality, aiding in operations and comparisons. |
Fractions and Mixed Numbers |

|
Video Definition 22--Fraction Concepts--Least Common Multiple (LCM) | Video Definition 22--Fraction Concepts--Least Common Multiple (LCM)
TopicFractions |
Fractions and Mixed Numbers |
|
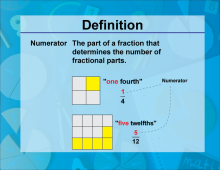
Video Definition 24--Fraction Concepts--Numerator | Video Definition 24--Fraction Concepts--Numerator
TopicFractions DescriptionThe term Numerator represents the part of a fraction that indicates how many parts of the whole are being considered. For example, in 1/4, the numerator is 1, meaning one part out of four. The image uses visual models to illustrate numerators in fractions like 1/4 and 5/12. Understanding the numerator is critical for interpreting the value of a fraction and applying it to real-world problems. |
Fractions and Mixed Numbers |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |

|
Video Definition 32--Fraction Concepts--Ratio | Video Definition 32--Fraction Concepts--Ratio
TopicFractions DescriptionA ratio is a comparison of two quantities or numbers by division, often written as a fraction. The image defines it as a / b, where b ≠ 0, and provides examples like 1 / 2 and 2 / 3. This term bridges fractions and their use in comparing quantities, which helps learners connect fraction concepts to real-world applications such as proportions and rates. |
Fractions and Mixed Numbers |

|
Video Definition 31--Fraction Concepts--Proper Fraction | Video Definition 31--Fraction Concepts--Proper Fraction
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 3--Fraction Concepts--Comparing Fractions | Video Definition 3--Fraction Concepts--Comparing Fractions
TopicFractions DescriptionComparing Fractions: Determining if one fraction is greater than, less than, or equal to another fraction. Examples demonstrate comparisons like 1/2 < 2/3 and 3/4 > 3/8. This concept reinforces understanding of relative size in fractions, a critical step in working with and manipulating fractions. |
Compare and Order Fractions |

|
Video Definition 16--Fraction Concepts--Fractional Exponents | Video Definition 16--Fraction Concepts--Fractional Exponents
TopicFractions DescriptionFractional exponents represent rational exponents, where the numerator indicates the power and the denominator indicates the root. Examples include 2(1/2) = √2 and 3(3/4) = (4th root of 33). These are used in advanced mathematical contexts like algebra and calculus. It introduces the connection between fractions and powers, extending the concept of fractions into exponential operations. |
Fractions and Mixed Numbers |

|
Video Definition 11--Fraction Concepts--Fraction in Simplest Form | Video Definition 11--Fraction Concepts--Fraction in Simplest Form
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 6--Fraction Concepts--Equivalent Fraction | Video Definition 6--Fraction Concepts--Equivalent Fraction
TopicFractions DescriptionEquivalent Fraction: A fraction with the same numerical value as another fraction, but whose numerator and denominator are multiplied by a common factor. Examples show 1/2 = 2/4 and 2/3 = 6/9. This term illustrates how fractions can be rewritten to have different forms while maintaining equality, aiding in operations and comparisons. |
Fractions and Mixed Numbers |

|
Video Definition 10--Fraction Concepts--Fraction Division | Video Definition 10--Fraction Concepts--Fraction Division
TopicFractions DescriptionFraction Division: Dividing one fraction by another. Fraction division can be written as a fraction product by using the reciprocal of the divisor. Examples include 1/2 ÷ 1/3 = 1/2 × 3/1 = 3/2. This operation builds on multiplication and introduces reciprocal concepts, expanding fraction operations. |
Fractions and Mixed Numbers |

|
Video Definition 33--Fraction Concepts--Rational Number | Video Definition 33--Fraction Concepts--Rational Number
TopicFractions DescriptionA rational number is defined as a ratio of two integers that can be expressed as a fraction, whole number, or decimal. Examples provided in the image include 0.5, 1 / 4, and 10. The term builds on the concept of ratios and fractions by showing that they can also represent rational numbers, broadening the application of fractions to include whole numbers and decimals. |
Fractions and Mixed Numbers |

|
Video Definition 24--Fraction Concepts--Numerator | Video Definition 24--Fraction Concepts--Numerator
TopicFractions DescriptionThe term Numerator represents the part of a fraction that indicates how many parts of the whole are being considered. For example, in 1/4, the numerator is 1, meaning one part out of four. The image uses visual models to illustrate numerators in fractions like 1/4 and 5/12. Understanding the numerator is critical for interpreting the value of a fraction and applying it to real-world problems. |
Fractions and Mixed Numbers |

|
Video Definition 31--Fraction Concepts--Proper Fraction | Video Definition 31--Fraction Concepts--Proper Fraction
TopicFractions |
Fractions and Mixed Numbers |
|
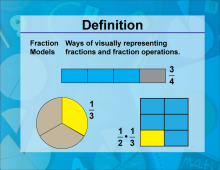
Video Definition 12--Fraction Concepts--Fraction Models | Video Definition 12--Fraction Concepts--Fraction Models
TopicFractions DescriptionFraction models visually represent fractions and operations. Examples include area models (shaded parts), bar models (partitioned sections), and multiplication models using grids. These provide a concrete way to understand and visualize fraction concepts. This builds on the concept of understanding fractions by providing a visual context, aiding comprehension of abstract fraction operations. |
Fractions and Mixed Numbers |

|
Video Definition 31--Fraction Concepts--Proper Fraction | Video Definition 31--Fraction Concepts--Proper Fraction
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 1--Fraction Concepts--Benchmark Fraction | Video Definition 1--Fraction Concepts--Benchmark Fraction
TopicFractions DescriptionBenchmark Fraction: A known fraction used to compare other fractions that are less than, greater than, or equal to it. The example given uses 1/2 as a benchmark. Fractions like 4/9 and 5/7 are compared to 1/2 on a number line, demonstrating that 4/9 < 1/2 and 5/7 > 1/2. This term helps students understand how to compare fractions using familiar reference points, a foundational skill in fraction concepts. |
Compare and Order Fractions |

|
Video Definition 1--Fraction Concepts--Benchmark Fraction | Video Definition 1--Fraction Concepts--Benchmark Fraction
TopicFractions DescriptionBenchmark Fraction: A known fraction used to compare other fractions that are less than, greater than, or equal to it. The example given uses 1/2 as a benchmark. Fractions like 4/9 and 5/7 are compared to 1/2 on a number line, demonstrating that 4/9 < 1/2 and 5/7 > 1/2. This term helps students understand how to compare fractions using familiar reference points, a foundational skill in fraction concepts. |
Compare and Order Fractions |

|
Video Definition 18--Fraction Concepts--Greatest Common Factor (GCF) | Video Definition 18--Fraction Concepts--Greatest Common Factor (GCF)
TopicFractions DescriptionThe Greatest Common Factor (GCF) is the largest number that divides two numbers evenly, used to simplify fractions. For example, the GCF of 24 and 36 is 12, enabling simplification of 24/36 to 2/3. This ensures fractions are in their simplest form. It supports simplifying fractions and ensures efficient fraction operations. |
Fractions and Mixed Numbers |

|
Video Definition 26--Fraction Concepts--Percent | Video Definition 26--Fraction Concepts--Percent
TopicFractions DescriptionThe term Percent represents a fraction with a denominator of 100, showing a proportion out of 100. Examples include 1% = 1/100, 5% = 5/100, and 25% = 25/100. Percentages are a real-world application of fractions and decimals, often used in data analysis, finance, and everyday calculations. |
Fractions and Mixed Numbers |

|
Video Definition 25--Fraction Concepts--Ordering Fractions | Video Definition 25--Fraction Concepts--Ordering Fractions
TopicFractions DescriptionThe term Ordering Fractions refers to arranging a set of fractions in ascending or descending order. The image provides examples of ordering fractions from least to greatest (1/5, 3/8, 1/2, 2/3) and greatest to least (7/8, 3/4, 2/3, 1/3). This term is important for comparing fractions and understanding their relative values, which is a fundamental skill in fraction operations. |
Compare and Order Fractions |

|
Video Definition 24--Fraction Concepts--Numerator | Video Definition 24--Fraction Concepts--Numerator
TopicFractions DescriptionThe term Numerator represents the part of a fraction that indicates how many parts of the whole are being considered. For example, in 1/4, the numerator is 1, meaning one part out of four. The image uses visual models to illustrate numerators in fractions like 1/4 and 5/12. Understanding the numerator is critical for interpreting the value of a fraction and applying it to real-world problems. |
Fractions and Mixed Numbers |

|
Video Definition 13--Fraction Concepts--Fraction Multiplication | Video Definition 13--Fraction Concepts--Fraction Multiplication
TopicFractions DescriptionFraction multiplication involves multiplying numerators and denominators directly. Examples include 1/2 * 1/3 = 1/6 and 3/4 * 4/4 = 3/16. This operation is fundamental for solving problems involving scaling and proportional reasoning. It connects to practical applications of fractions in areas such as ratios, rates, and scaling. |
Fractions and Mixed Numbers |

|
Video Definition 4--Fraction Concepts--Decimal Fraction | Video Definition 4--Fraction Concepts--Decimal Fraction
TopicFractions DescriptionDecimal Fraction: A fraction expressed as a decimal number, typically with a terminating or repeating decimal representation. Examples include 1/2 = 0.5, 3/4 = 0.75, and 1/3 = 0.333... This term bridges fractions and decimals, showing their equivalence and preparing students for broader applications in mathematics. |
Fractions and Mixed Numbers |

|
Video Definition 31--Fraction Concepts--Proper Fraction | Video Definition 31--Fraction Concepts--Proper Fraction
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 35--Fraction Concepts--Unit Fraction | Video Definition 35--Fraction Concepts--Unit Fraction
TopicFractions DescriptionA unit fraction is a fraction whose numerator is 1 and whose denominator is a whole number. The image provides examples like 1 / 2, 1 / 3, and 1 / 4, and explains that any fraction can be written as the sum of unit fractions. This term highlights the simplicity of unit fractions as building blocks for other fractions, reinforcing the idea that complex fractions can be deconstructed into simpler parts. |
Fractions and Mixed Numbers |

|
Video Definition 8--Fraction Concepts--Fraction Addition | Video Definition 8--Fraction Concepts--Fraction Addition
TopicFractions DescriptionFraction Addition: Combining two or more fractions whose sum is another fraction, mixed number, or whole number. Examples include 1/2 + 1/3 = 5/6 and 1 1/3 + 3/4 = 1 11/12. This operation demonstrates how fractions interact arithmetically, an important skill for problem-solving. |
Fractions and Mixed Numbers |

|
Video Definition 30--Fraction Concepts--Percentage Increase | Video Definition 30--Fraction Concepts--Percentage Increase
TopicFractions DescriptionThe term Percentage Increase refers to the increase in value expressed as a percentage of the original value. The example shows an increase from 25 to 40, calculated as (40 - 25) / 25 * 100%, which equals 60%. This term reinforces the application of percentages and fractions in scenarios like profit and growth analysis. |
Fractions and Mixed Numbers |

|
Video Definition 7--Fraction Concepts--Fraction | Video Definition 7--Fraction Concepts--Fraction
TopicFractions DescriptionFraction: A number representing part of a whole, usually written as the ratio of a numerator and a non-zero denominator. Examples include 4/16, 3/4, and 7/4, with visuals explaining numerator and denominator. This foundational term establishes the basic structure and meaning of fractions, essential for all subsequent fraction concepts. |
Fractions and Mixed Numbers |

|
Video Definition 21--Fraction Concepts--Least Common Denominator (LCD) | Video Definition 21--Fraction Concepts--Least Common Denominator (LCD)
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 25--Fraction Concepts--Ordering Fractions | Video Definition 25--Fraction Concepts--Ordering Fractions
TopicFractions DescriptionThe term Ordering Fractions refers to arranging a set of fractions in ascending or descending order. The image provides examples of ordering fractions from least to greatest (1/5, 3/8, 1/2, 2/3) and greatest to least (7/8, 3/4, 2/3, 1/3). This term is important for comparing fractions and understanding their relative values, which is a fundamental skill in fraction operations. |
Compare and Order Fractions |

|
Video Definition 21--Fraction Concepts--Least Common Denominator (LCD) | Video Definition 21--Fraction Concepts--Least Common Denominator (LCD)
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |

|
Video Definition 27--Fraction Concepts--Percent Error | Video Definition 27--Fraction Concepts--Percent Error
TopicFractions DescriptionThe term Percent Error describes the difference between an estimated value and the actual value, expressed as a percentage of the actual value. The example provided shows an estimated value of 100 versus an actual value of 107, resulting in a percent error of approximately 6.54%. This concept links fractions, percentages, and error analysis, which are important in measurement and data accuracy. |
Fractions and Mixed Numbers |

|
Video Definition 7--Fraction Concepts--Fraction | Video Definition 7--Fraction Concepts--Fraction
TopicFractions DescriptionFraction: A number representing part of a whole, usually written as the ratio of a numerator and a non-zero denominator. Examples include 4/16, 3/4, and 7/4, with visuals explaining numerator and denominator. This foundational term establishes the basic structure and meaning of fractions, essential for all subsequent fraction concepts. |
Fractions and Mixed Numbers |

|
Video Definition 22--Fraction Concepts--Least Common Multiple (LCM) | Video Definition 22--Fraction Concepts--Least Common Multiple (LCM)
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |

|
Video Definition 22--Fraction Concepts--Least Common Multiple (LCM) | Video Definition 22--Fraction Concepts--Least Common Multiple (LCM)
TopicFractions |
Fractions and Mixed Numbers |

|
Video Definition 17--Fraction Concepts--Fractions As Division | Video Definition 17--Fraction Concepts--Fractions As Division
TopicFractions DescriptionFractions as division represent the numerator divided by the denominator. Examples include 3/2 = 3 ÷ 2 = 1.5 and 4/5 = 4 ÷ 5 = 0.8. This representation helps convert fractions to decimals and understand their equivalence. This illustrates the dual nature of fractions as division, enhancing understanding of fractions in both numerical and decimal contexts. |
Fractions and Mixed Numbers |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |

|
Video Definition 25--Fraction Concepts--Ordering Fractions | Video Definition 25--Fraction Concepts--Ordering Fractions
TopicFractions DescriptionThe term Ordering Fractions refers to arranging a set of fractions in ascending or descending order. The image provides examples of ordering fractions from least to greatest (1/5, 3/8, 1/2, 2/3) and greatest to least (7/8, 3/4, 2/3, 1/3). This term is important for comparing fractions and understanding their relative values, which is a fundamental skill in fraction operations. |
Compare and Order Fractions |

|
Video Definition 28--Fraction Concepts--Percentage | Video Definition 28--Fraction Concepts--Percentage
TopicFractions DescriptionThe term Percentage refers to converting fractions and decimals into their equivalent percentages. Examples include 1/2 = 50%, 0.4 = 40%, and 1/3 ≈ 33.3%. This concept connects fractions, decimals, and percentages, emphasizing their equivalence and usage in various contexts. |
Fractions and Mixed Numbers |

|
Video Definition 3--Fraction Concepts--Comparing Fractions | Video Definition 3--Fraction Concepts--Comparing Fractions
TopicFractions DescriptionComparing Fractions: Determining if one fraction is greater than, less than, or equal to another fraction. Examples demonstrate comparisons like 1/2 < 2/3 and 3/4 > 3/8. This concept reinforces understanding of relative size in fractions, a critical step in working with and manipulating fractions. |
Compare and Order Fractions |

|
Video Definition 34--Fraction Concepts--Reciprocal | Video Definition 34--Fraction Concepts--Reciprocal
TopicFractions DescriptionA reciprocal is the multiplicative inverse of a number, obtained by swapping the numerator and denominator of a fraction. Examples include the reciprocals 2 / 3 and 3 / 2, as well as 4 / 5 and 5 / 4. This term connects to operations with fractions, especially in division and multiplication, where understanding reciprocals is essential for solving equations and simplifying expressions. |
Fractions and Mixed Numbers |

|
Video Definition 20--Fraction Concepts--Irrational Number | Video Definition 20--Fraction Concepts--Irrational Number
TopicFractions DescriptionAn irrational number cannot be expressed as a fraction and has a non-terminating, non-repeating decimal form. Examples include π = 3.14159... and √2 = 1.41421.... This highlights the contrast between rational and irrational numbers. This connects fractions to the broader number system, emphasizing differences in numerical properties. |
Fractions and Mixed Numbers |
|
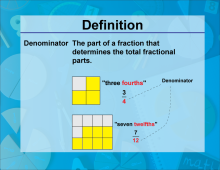
Video Definition 5--Fraction Concepts--Denominator | Video Definition 5--Fraction Concepts--Denominator
TopicFractions DescriptionDenominator: The part of a fraction that determines the total fractional parts. Visuals show fractions like 3/4 ('three fourths') and 7/12 ('seven twelfths') with denominators highlighted. Understanding the denominator is crucial for interpreting fractions and performing operations like comparison and simplification. |
Fractions and Mixed Numbers |
|
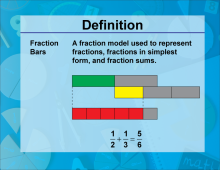
Video Definition 9--Fraction Concepts--Fraction Bars | Video Definition 9--Fraction Concepts--Fraction Bars
TopicFractions DescriptionFraction Bars: A fraction model used to represent fractions, fractions in simplest form, and fraction sums. The visual illustrates 1/2 + 1/3 = 5/6 using colored bars. This visual model aids in conceptual understanding of fraction operations and relationships. |
Fractions and Mixed Numbers |

|
Video Definition 5--Fraction Concepts--Denominator | Video Definition 5--Fraction Concepts--Denominator
TopicFractions DescriptionDenominator: The part of a fraction that determines the total fractional parts. Visuals show fractions like 3/4 ('three fourths') and 7/12 ('seven twelfths') with denominators highlighted. Understanding the denominator is crucial for interpreting fractions and performing operations like comparison and simplification. |
Fractions and Mixed Numbers |

|
Video Definition 5--Fraction Concepts--Denominator | Video Definition 5--Fraction Concepts--Denominator
TopicFractions DescriptionDenominator: The part of a fraction that determines the total fractional parts. Visuals show fractions like 3/4 ('three fourths') and 7/12 ('seven twelfths') with denominators highlighted. Understanding the denominator is crucial for interpreting fractions and performing operations like comparison and simplification. |
Fractions and Mixed Numbers |