
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 17: Fitting Boxes into Boxes
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Worksheet: Writing Fractions in Simplest Form, Worksheet 1 | Worksheet: Writing Fractions in Simplest Form, Worksheet 1
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Write Fractions in Lowest Terms |

|
Worksheet: Writing Fractions, Worksheet 2 | Worksheet: Writing Fractions, Worksheet 2
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Worksheet: Writing Fractions, Worksheet 2 | Worksheet: Writing Fractions, Worksheet 2
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Worksheet: Writing Fractions, Worksheet 2 | Worksheet: Writing Fractions, Worksheet 2
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Worksheet: Writing Fractions, Worksheet 1 | Worksheet: Writing Fractions, Worksheet 1
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Worksheet: Writing Fractions, Worksheet 1 | Worksheet: Writing Fractions, Worksheet 1
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Worksheet: Writing Fractions, Worksheet 1 | Worksheet: Writing Fractions, Worksheet 1
This is part of a collection of math worksheets on the topic of writing fractions. To see the complete worksheet collection on this topic, click on this link. Note: The download is a PDF file.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Worksheet LibraryTo see the complete collection of Worksheets, click on this link. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Crossword Puzzle: Fractions | Interactive Crossword Puzzle: Fractions
Review key vocabulary on the topic of fractions with this interactive and printable crossword puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Interactive Word Search Puzzle: Fractions Puzzle 1 | Interactive Word Search Puzzle: Fractions Puzzle 1
Review key vocabulary on the topic of fractions with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Fractions and Mixed Numbers |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |
|
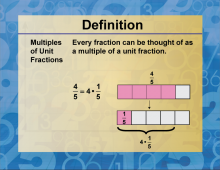
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |

|
Definition--Fraction Concepts--Unit Fraction | Unit FractionTopicFractions DefinitionA unit fraction is a fraction where the numerator is 1 and the denominator is a positive integer. DescriptionA unit fraction is a fundamental concept in the study of fractions and plays a crucial role in understanding more complex fractional operations. It represents one part of a whole that has been divided into equal parts. For example, the unit fraction 1/4 means one part of a whole that is divided into four equal parts. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Equivalent Fraction | Equivalent FractionsTopicFractions DefinitionEquivalent fractions are fractions that represent the same part of a whole, even though they may have different numerators and denominators. DescriptionEquivalent fractions are fundamental in understanding the concept of fractions in mathematics. They are fractions that, although they may look different, actually represent the same value. For example, the fractions 1/2 and 2/4 are equivalent because they both represent the same portion of a whole. This concept is crucial for various mathematical operations and problem-solving techniques. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Unit Fraction | Unit FractionTopicFractions DefinitionA unit fraction is a fraction where the numerator is 1 and the denominator is a positive integer. DescriptionA unit fraction is a fundamental concept in the study of fractions and plays a crucial role in understanding more complex fractional operations. It represents one part of a whole that has been divided into equal parts. For example, the unit fraction 1/4 means one part of a whole that is divided into four equal parts. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Equivalent Fraction | Equivalent FractionsTopicFractions DefinitionEquivalent fractions are fractions that represent the same part of a whole, even though they may have different numerators and denominators. DescriptionEquivalent fractions are fundamental in understanding the concept of fractions in mathematics. They are fractions that, although they may look different, actually represent the same value. For example, the fractions 1/2 and 2/4 are equivalent because they both represent the same portion of a whole. This concept is crucial for various mathematical operations and problem-solving techniques. |
Fractions and Mixed Numbers |
|
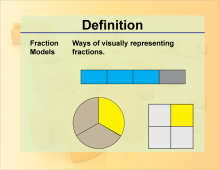
Definition--Fraction Concepts--Fraction Models | Fraction ModelsTopicFractions DefinitionFraction models are visual representations used to illustrate the concept of fractions, showing parts of a whole. DescriptionFraction models play a crucial role in understanding and teaching fractions. These models provide a visual representation that helps students grasp the idea of parts of a whole, which is fundamental in fraction concepts. There are several types of fraction models, including area models, set models, and number lines. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Least Common Multiple (LCM) | Least Common Multiple (LCM)TopicFractions DefinitionThe Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of each of the numbers. DescriptionThe concept of the Least Common Multiple (LCM) is fundamental in the study of fractions. It is particularly useful when adding, subtracting, or comparing fractions. The LCM helps in finding a common denominator, which is essential for performing these operations with fractions. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Least Common Multiple (LCM) | Least Common Multiple (LCM)TopicFractions DefinitionThe Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of each of the numbers. DescriptionThe concept of the Least Common Multiple (LCM) is fundamental in the study of fractions. It is particularly useful when adding, subtracting, or comparing fractions. The LCM helps in finding a common denominator, which is essential for performing these operations with fractions. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Fraction in Simplest Form | Fraction in Simplest FormTopicFractions DefinitionA fraction is in its simplest form when the numerator and denominator have no common divisor other than 1. DescriptionIn mathematics, fractions represent parts of a whole. A fraction is composed of a numerator (the top number) and a denominator (the bottom number). Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. For example, the fraction 4/8 can be simplified to 1/2 by dividing both the numerator and the denominator by their greatest common divisor, which is 4. |
Fractions and Mixed Numbers |

|
Definition--Fraction Concepts--Least Common Multiple (LCM) | Least Common Multiple (LCM)TopicFractions DefinitionThe Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of each of the numbers. DescriptionThe concept of the Least Common Multiple (LCM) is fundamental in the study of fractions. It is particularly useful when adding, subtracting, or comparing fractions. The LCM helps in finding a common denominator, which is essential for performing these operations with fractions. |
Fractions and Mixed Numbers |