Illustrative Math Alignment: Grade 6 Unit 9

This is the transcript for the video of same title. Video contents: In this program we explore the properties of quadrilaterals. We do this in the context of two real-world applications. In the first, we explore the architecture of Frank Lloyd Wright as an application of squares and rectangles; in particular, we look at his Fallingwater house. In the second application we look at a unique parallelogram-shaped building in Spain, known as the Puerta de Europa. It provides an opportunity to explore the properties of parallelograms and trapezoids.

This is the transcript for the video of same title. Video contents: Stonehenge is best known as a circular structure. But it's the post and lintel construction used that is noteworthy, and this type of construction involves quadrilateral shapes. From the familiar door frames of houses to the majestic entryways of ancient temples, post and lintel construction provides a clear introduction to the nature of quadrilaterals. This segment also describes the key concepts developed throughout the program.

This is the transcript for the video of same title. Video contents: Frank Lloyd Wright's architectural masterpiece Falling Water is also a stunning assembly of quadrilateral shapes. Some of the rectangular forms in this building seem to defy gravity, as we explore the properties of squares and rectangles that allowed Frank Lloyd Wright to push the envelope of design and structure.

This is the transcript for the video of same title. Video contents: The Puerta de Europa towers in Madrid bring parallelograms front and center. These tilted towers, looking like modern-day towers of Pisa seem to defy gravity, but rely on the stability brought about by its quadrilateral structure. The underlying parallelogram and trapezoidal designs are explored and analyzed.

Topic

Geometry

Description

This example presents a quadrilateral with labeled sides: AB = 5, BC = 4, CD = 3, and DA = 6. The task is to classify the quadrilateral based on these measurements. Since none of the sides are congruent and no specific relationships among the sides can be determined, this shape is classified as a generic quadrilateral.

Topic

Geometry

Description

This example showcases a quadrilateral with sides labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the sides are given, and no sides are stated to be congruent, this shape is classified as a generic quadrilateral.

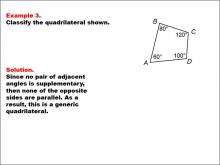
Topic

Geometry

Description

This example presents a quadrilateral with labeled angles: A = 60°, B = 80°, C = 120°, and D = 100°. The task is to classify the quadrilateral based on these angle measurements. Since no pair of adjacent angles is supplementary (adds up to 180°), none of the opposite sides are parallel. As a result, this shape is classified as a generic quadrilateral.

Topic

Geometry

Description

This example features a quadrilateral with angles labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the angles are given, and no angles are stated to be congruent or supplementary, this shape is classified as a generic quadrilateral.

Topic

Geometry

Description

This example presents a quadrilateral with no right angles or congruent sides, labeled with angles and side lengths. The task is to classify the quadrilateral based on these characteristics. Since no adjacent angles are supplementary and no sides are parallel, this shape is classified as a generic quadrilateral.

Topic

Geometry

Description

This example showcases a rectangle with opposite sides labeled as 3 and 1, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As the shape has opposite sides that are congruent and all interior angles are 90 degrees, it is identified as a rectangle.

Topic

Geometry

Description

This example presents a rectangle with opposite sides labeled x and y, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. Due to the congruent opposite sides and all interior angles being 90 degrees, this shape is identified as a rectangle.

Topic

Geometry

Description

This example features a rectangle with sides labeled 7 and 5, and all angles are right angles. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and opposite sides are parallel and congruent, this shape is confirmed to be a rectangle.

Topic

Geometry

Description

This example presents a quadrilateral with all right angles, labeled as A, B, C, and D. The opposite sides are parallel and congruent. Based on these characteristics, the shape is classified as a rectangle. All interior angles are 90 degrees, and the opposite sides are both parallel and congruent, which are defining properties of a rectangle.

Topic

Geometry

Description

This example showcases a quadrilateral with right angles labeled with variable x at two corners, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This means all angles are 90 degrees. Since opposite sides are parallel and congruent, we can classify this shape as a rectangle.

Topic

Geometry

Description

This example presents a square with all sides congruent and right angles, labeled as A, B, C, and D. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and all sides are congruent, this shape is confirmed to be a square.

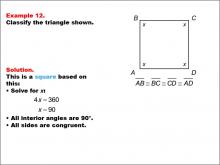
Topic

Geometry

Description

This example features a quadrilateral with all sides labeled x and marked congruent, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 4x = 360, which gives us x = 90. This means all angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square.

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. To classify this shape, we solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This confirms that all interior angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square.

Topic

Geometry

Description

This example showcases a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. Each side is labeled with a length of 1. Based on these characteristics, we can classify this shape as a square. All sides are congruent, which means opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees.

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. Based on these characteristics, we can classify this shape as a square. Because all sides are congruent, opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees.

Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with two sides labeled with lengths of 5 and x, and angles marked as right angles. The diagram shows perpendicular lines and parallel lines. Based on these characteristics, we can classify this shape as a square. Because angle ABC and angle BAD are supplementary, BC and AD are parallel. Since AB and CD are congruent, angle BAD and angle ADC are supplementary. Therefore, all interior angles are 90 degrees, and all sides are congruent.

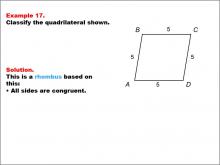
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as 5 units, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The key property that defines a rhombus is that all sides are congruent, which is clearly demonstrated in this example.

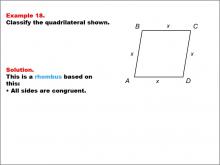
Topic

Geometry

Description

This example showcases a quadrilateral labeled ABCD with all sides marked as x, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The defining property of a rhombus is that all sides are congruent, which is clearly demonstrated in this example by using the variable x for all side lengths.

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides AB and CD marked as x, and BC and AD marked as 5. Opposite sides are noted to be parallel. Based on these characteristics, we can classify this shape as a rhombus. The key properties that define this as a rhombus are: opposite sides are parallel, and opposite sides are congruent. Since x = 5, all sides are congruent, which is a defining property of a rhombus.

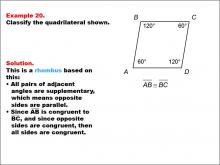
Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with angles B and D marked as 120 degrees, and angles A and C as 60 degrees. Sides AB and BC are marked as congruent. Based on these characteristics, we can classify this shape as a rhombus. All pairs of adjacent angles are supplementary (120° + 60° = 180°), which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus.

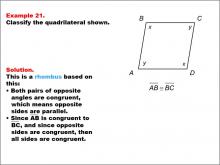
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent, all sides must be congruent, defining this shape as a rhombus.

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with angles marked as 70° and sides marked as x. Opposite angles are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus.

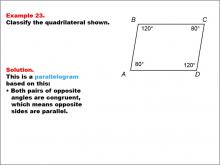
Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with angles marked as 120° and 80°. Opposite angles are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms.

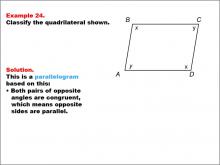
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite sides are congruent, which means opposite sides are parallel, a defining property of parallelograms.

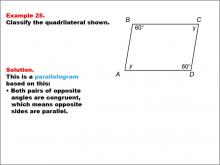
Topic

Geometry

Description

This example showcases a quadrilateral labeled ABCD with angles at B and D marked as 60 degrees. Sides AD and BC are labeled y. The shape is identified as a parallelogram. This classification is based on the fact that both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms.

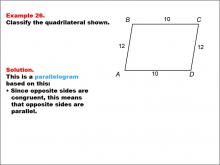
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides AB and CD measuring 10, and sides BC and AD measuring 12. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms.

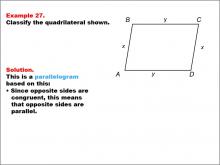
Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with sides AB and CD labeled y, and sides AD and BC labeled x. The shape is identified as a parallelogram. This classification is based on the fact that opposite sides are congruent, which means that opposite sides are parallel, a defining property of parallelograms.

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides BC and AD parallel, and AB and CD parallel. Side BC is marked as 5, and side AD is marked as x. Based on these characteristics, we can classify this shape as a parallelogram. Opposite sides are parallel (BC // AD, AB // CD), which is the defining property of a parallelogram. However, adjacent sides are not necessarily congruent, as BC is 5 and AD is x.

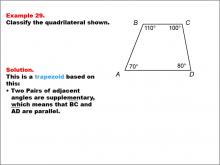
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with angles marked as 110°, 100°, 70°, and 80°. Two pairs of adjacent angles are supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel.

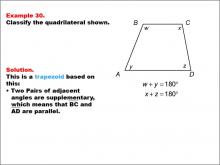
Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with angles marked as w, x, y, and z. It states that w + y = 180° and x + z = 180°. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel.

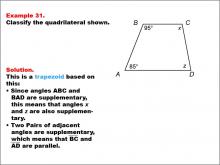
Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with angles ABC = 95° and BAD = 85°. It states that angles x and z are also supplementary due to two pairs of adjacent angles being supplementary. Based on these characteristics, we can classify this shape as a trapezoid. The key property that defines this as a trapezoid is that two pairs of adjacent angles are supplementary, which means that BC and AD are parallel.

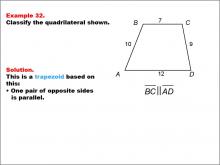
Topic

Geometry

Description

This example showcases a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 10, BC = 7, CD = 9, and AD = 12. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel.

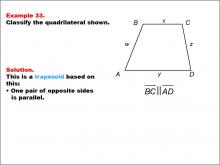
Topic

Geometry

Description

This example presents a trapezoid with vertices labeled A, B, C, D. The sides are labeled as w, x, y, and z. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel.

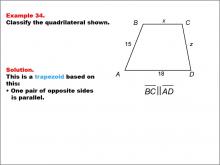
Topic

Geometry

Description

This example features a trapezoid with vertices labeled A, B, C, D. The side lengths are given as AB = 15, BC = x, CD = z, and AD = 18. It is stated that BC and AD are parallel. Based on these characteristics, we can confirm that this shape is indeed a trapezoid. The key property that defines this as a trapezoid is that one pair of opposite sides (BC and AD) are parallel.

Topic

Geometry

Description

This example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units.

Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter.

Topic

Geometry

Description

This example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units.

Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation.

Topic

Geometry

Description

This example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units.

Topic

Geometry

Description

This example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units.

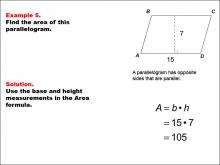
Topic

Geometry

Description

This example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units.

Topic

Geometry

Description

This example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units.

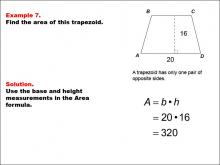
Topic

Geometry

Description

This example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units.

Topic

Geometry

Description

This example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units.

Topic

Geometry

Description

This example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units.

Topic

Geometry

Description

This example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units.

Topic

Geometry

Description

This example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units.

Topic

Geometry

Description

This example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units.