Illustrative Math Alignment: Grade 6 Unit 9

Topic

Geometry

Description

This example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units.

Topic

Geometry

Description

This example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units.

Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses.

Topic

Geometry

Description

This example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units.

Topic

Geometry

Description

This example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units.

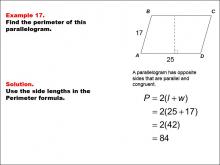
Topic

Geometry

Description

This example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units.

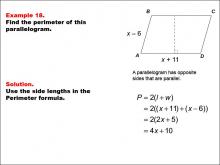
Topic

Geometry

Description

This example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units.

Topic

Geometry

Description

This example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units.

Topic

Geometry

Description

This example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units.

Topic

Geometry

Description

This example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units.

Topic

Geometry

Description

This example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units.

Topic

Geometry

Description

This example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units.

Topic

Geometry

Description

This example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units.

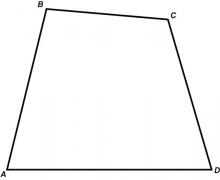
Topic

Geometry Concepts

Description

This image illustrates a generic quadrilateral, a four-sided polygon with no specific properties regarding side lengths or angles. Quadrilaterals are a fundamental shape in geometry, and their properties can vary widely.

Understanding generic quadrilaterals is crucial for exploring the properties of more specific types, such as squares, rectangles, and trapezoids. They serve as a basis for studying angles, side lengths, and symmetry in polygons.

Topic

Geometry Concepts

Description

This image depicts a rectangle, a quadrilateral with opposite sides that are equal and parallel, and four right angles. Rectangles are a specific type of quadrilateral with symmetrical properties and are widely used in design and architecture.

Understanding rectangles involves exploring properties such as area, perimeter, and symmetry. They are used in various mathematical contexts to study parallel lines, congruence, and transformations.

Topic

Geometry Concepts

Description

This image features a rhombus, a quadrilateral with all sides equal in length and opposite angles equal. Rhombuses are a specific type of parallelogram with unique symmetrical properties.

Understanding rhombuses involves exploring properties such as area, perimeter, and symmetry. They are used in various mathematical contexts to study congruence, transformations, and tiling patterns.

Teacher's Script: "Examine this rhombus. How do its properties, such as equal sides and opposite angles, help us understand its geometry? What are some mathematical concepts you can explore using rhombuses, such as symmetry or transformations?"

Topic

Geometry Concepts

Description

This image depicts a square, a quadrilateral with all sides equal and all angles equal to 90 degrees. Squares are a specific type of rectangle and rhombus, known for their perfect symmetry and balance.

Understanding squares involves exploring properties such as area, perimeter, and symmetry. They are used in various mathematical contexts to study congruence, transformations, and tiling patterns.

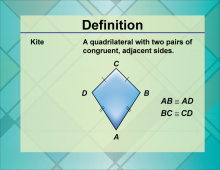
Teacher's Script: "Look at this square. How do its properties, such as equal sides and right angles, help us understand its geometry? What are some real-world applications of squares, such as in design or architecture?"

Topic

Quadrilaterals

Definition

A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal.

Description

Kites are unique geometric figures that play a significant role in both theoretical and applied mathematics. The properties of kites are utilized in real-world applications, such as in design and computer graphics. Moreover, understanding kites enhances students' grasp of more advanced geometric properties and relationships, making this concept highly relevant in math education.

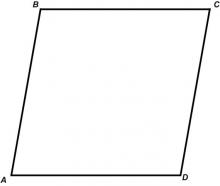
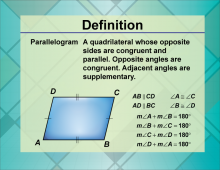
Topic

Quadrilaterals

Definition

A parallelogram is a quadrilateral with opposite sides that are equal and parallel.

Description

Parallelograms hold significant importance in both theoretical and applied mathematics. They are observed in various real-world situations such as architecture and engineering designs. Understanding the properties of parallelograms forms a foundation for more complex geometric concepts that students will encounter in their education, which highlights their relevance in mathematics teaching.

Topic

Quadrilaterals

Definition

A quadrilateral is a four-sided polygon characterized by its vertices and edges.

Description

Quadrilaterals are foundational shapes in geometry that underpin more advanced concepts. Utilizing quadrilaterals in both theoretical models and real-world applications, such as in architecture and design, exemplifies their significance. Grasping the properties of quadrilaterals helps students build essential reasoning skills necessary in various fields of math and science, emphasizing the need for a strong understanding of geometric principles.

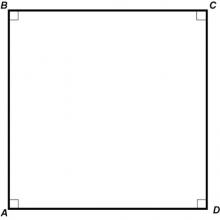
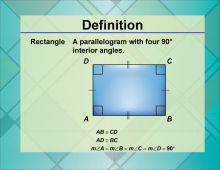
Topic

Quadrilaterals

Definition

A rectangle is a quadrilateral with opposite sides equal and four right angles.

Description

Rectangles are one of the most common geometric shapes, greatly used across different domains including art, architecture, and various forms of design. Understanding the properties and applications of rectangles is crucial in math education as they form a basis for learning about more complex geometric shapes. Mastery of rectangles allows students to develop spatial understanding and problem-solving skills needed for more advanced math topics.

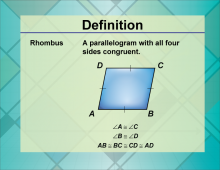
Topic

Quadrilaterals

Definition

A rhombus is a quadrilateral with all sides equal in length.

Description

The rhombus, with its unique properties, serves as an integral concept in geometry. Its applications span design and manufacturing industries, where equal lengths are essential. Assuring that students understand the rhombus furthers their grasp of geometric properties and relationships, underpinning more advanced learning in mathematics education.

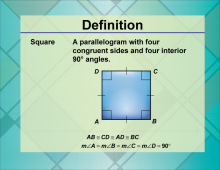
Topic

Quadrilaterals

Definition

A square is a quadrilateral with all four sides of equal length and all four angles equal to 90 degrees.

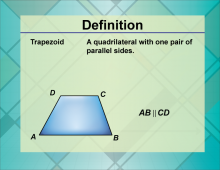
Topic

Quadrilaterals

Definition

A trapezoid is a quadrilateral with at least one pair of parallel sides.

Description

The trapezoid is a versatile geometric shape with applications in various fields such as architecture, engineering, and art. Its defining feature is having one pair of parallel sides, which makes it useful for creating structures and designs that require stability and balance. Understanding trapezoids helps students grasp the concept of parallelism and its implications in geometry. This knowledge is vital for solving real-world problems and enhances students' overall mathematical proficiency.

Use this math game to review quadrilaterals. This is a Memory-style game in which students must remember the location of pairs of identical images.

Related Resources

This interactive crossword puzzle tests knowledge of key terms on the topic of quadrilaterals.

Related Resources

In this program we explore the properties of quadrilaterals. We do this in the context of two real-world applications. In the first, we explore the architecture of Frank Lloyd Wright as an application of squares and rectangles; in particular, we look at his Fallingwater house. In the second application we look at a unique parallelogram-shaped building in Spain, known as the Puerta de Europa. It provides an opportunity to explore the properties of parallelograms and trapezoids.

Stonehenge is best known as a circular structure. But it’s the post and lintel construction used that is noteworthy, and this type of construction involves quadrilateral shapes. From the familiar door frames of houses to the majestic entryways of ancient temples, post and lintel construction provides a clear introduction to the nature of quadrilaterals. This segment also describes the key concepts developed throughout the program.

Frank Lloyd Wright’s architectural masterpiece Falling Water is also a stunning assembly of quadrilateral shapes. Some of the rectangular forms in this building seem to defy gravity, as we explore the properties of squares and rectangles that allowed Frank Lloyd Wright to push the envelope of design and structure.

The Puerta de Europa towers in Madrid bring parallelograms front and center. These tilted towers, looking like modern-day towers of Pisa seem to defy gravity, but rely on the stability brought about by its quadrilateral structure. The underlying parallelogram and trapezoidal designs are explored and analyzed.