Illustrative Math Alignment: Grade 7 Unit 3

Measuring Circles

Lesson 1: How Well Can You Measure?

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Definition--Circle Concepts--Circles on a Coordinate Plane	Circles on a Coordinate Plane Topic Circles Definition Circles on a coordinate plane are defined by their center coordinates and radius. Description Understanding circles on a coordinate plane is essential for analyzing geometric shapes in a mathematical context. This concept is widely used in computer graphics, navigation systems, and physics simulations, where precise positioning and movement of circular objects are required. The standard equation of a circle in the coordinate plane is (x − h)2 + (y − k)2 = r2	Definition of a Circle
Definition--Circle Concepts--Circles on a Coordinate Plane	Circles on a Coordinate Plane Topic Circles Definition Circles on a coordinate plane are defined by their center coordinates and radius. Description Understanding circles on a coordinate plane is essential for analyzing geometric shapes in a mathematical context. This concept is widely used in computer graphics, navigation systems, and physics simulations, where precise positioning and movement of circular objects are required. The standard equation of a circle in the coordinate plane is (x − h)2 + (y − k)2 = r2	Definition of a Circle
Definition--Circle Concepts--Circles on a Coordinate Plane	Circles on a Coordinate Plane Topic Circles Definition Circles on a coordinate plane are defined by their center coordinates and radius. Description Understanding circles on a coordinate plane is essential for analyzing geometric shapes in a mathematical context. This concept is widely used in computer graphics, navigation systems, and physics simulations, where precise positioning and movement of circular objects are required. The standard equation of a circle in the coordinate plane is (x − h)2 + (y − k)2 = r2	Definition of a Circle
Definition--Circle Concepts--Circular Cross-Sections	Circular Cross-Sections Topic Circles Definition Circular cross-sections are the intersections of a plane with a solid that result in a circle.	Definition of a Circle
Definition--Circle Concepts--Circular Cross-Sections	Circular Cross-Sections Topic Circles Definition Circular cross-sections are the intersections of a plane with a solid that result in a circle.	Definition of a Circle
Definition--Circle Concepts--Circular Cross-Sections	Circular Cross-Sections Topic Circles Definition Circular cross-sections are the intersections of a plane with a solid that result in a circle.	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
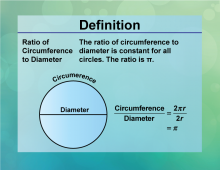
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
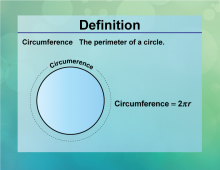
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
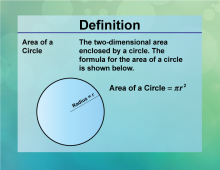
Definition--Circle Concepts--Area of a Circle	Area of a Circle Topic Circles Definition The area of a circle is the space contained within its circumference, calculated as A = πr2 Description The area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula A = πr2	Definition of a Circle
Definition--Circle Concepts--Area of a Circle	Area of a Circle Topic Circles Definition The area of a circle is the space contained within its circumference, calculated as A = πr2 Description The area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula A = πr2	Definition of a Circle
Definition--Circle Concepts--Area of a Circle	Area of a Circle Topic Circles Definition The area of a circle is the space contained within its circumference, calculated as A = πr2 Description The area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula A = πr2	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
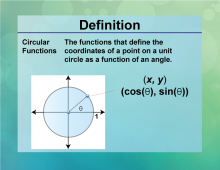
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
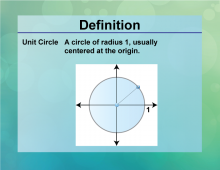
Definition--Circle Concepts--Unit Circle	Unit Circle Topic Circles Definition The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane.	Definition of a Circle
Definition--Circle Concepts--Unit Circle	Unit Circle Topic Circles Definition The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane.	Definition of a Circle
Definition--Circle Concepts--Unit Circle	Unit Circle Topic Circles Definition The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane.	Definition of a Circle
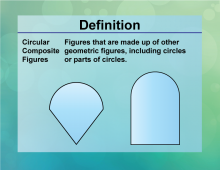
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
Definition--Circle Concepts--Circular Composite Figures	Circular Composite Figures Topic Circles Definition Circular composite figures are shapes that include circles or parts of circles combined with other geometric figures.	Definition of a Circle
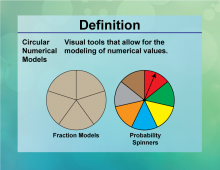
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
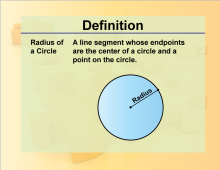
Definition--Geometry Basics--Radius	Radius Topic Geometry Basics Definition The radius is the distance from the center to any point on the circumference of a circle. Description Calculating the radius is fundamental in determining properties related to circles, including area and circumference. The radius can also serve as a critical parameter in various applications ranging from designing circular objects in engineering to understanding phenomena like waves in physics. In contexts such as statistics or data science, circle properties often illustrate core concepts visually speaking to broader trends.	Definition of a Circle
Definition--Geometry Basics--Radius	Radius Topic Geometry Basics Definition The radius is the distance from the center to any point on the circumference of a circle. Description Calculating the radius is fundamental in determining properties related to circles, including area and circumference. The radius can also serve as a critical parameter in various applications ranging from designing circular objects in engineering to understanding phenomena like waves in physics. In contexts such as statistics or data science, circle properties often illustrate core concepts visually speaking to broader trends.	Definition of a Circle
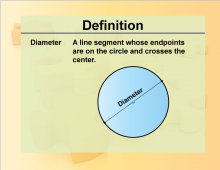
Definition--Geometry Basics--Diameter	Diameter Topic Geometry Basics Definition The diameter of a circle is the longest distance across the circle, passing through the center. Description The diameter is twice the radius of a circle and is a fundamental concept in circle geometry. The formula for the diameter is d = 2r, where r is the radius. Understanding the diameter is crucial for solving problems related to the circumference and area of circles. For example, the circumference of a circle can be calculated using the formula C = πd. This concept is used in various real-world applications, such as engineering and design, to ensure precision and accuracy in circular objects.	Definition of a Circle
Definition--Geometry Basics--Diameter	Diameter Topic Geometry Basics Definition The diameter of a circle is the longest distance across the circle, passing through the center. Description The diameter is twice the radius of a circle and is a fundamental concept in circle geometry. The formula for the diameter is d = 2r, where r is the radius. Understanding the diameter is crucial for solving problems related to the circumference and area of circles. For example, the circumference of a circle can be calculated using the formula C = πd. This concept is used in various real-world applications, such as engineering and design, to ensure precision and accuracy in circular objects.	Definition of a Circle
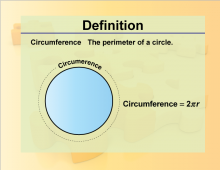
Definition--Geometry Basics--Circumference	Circumference Topic Geometry Basics Definition The distance around the edge of a circle. Description The circumference is the distance around the edge of a circle. This concept is fundamental in understanding the properties of circles and their measurements. The formula for the circumference is C = 2πr, where r is the radius of the circle. Understanding the circumference is crucial for solving problems related to circle geometry, such as finding the length of an arc or the area of a sector.	Definition of a Circle
Definition--Geometry Basics--Circumference	Circumference Topic Geometry Basics Definition The distance around the edge of a circle. Description The circumference is the distance around the edge of a circle. This concept is fundamental in understanding the properties of circles and their measurements. The formula for the circumference is C = 2πr, where r is the radius of the circle. Understanding the circumference is crucial for solving problems related to circle geometry, such as finding the length of an arc or the area of a sector.	Definition of a Circle
Math Definitions Collection: Circles	Overview The collection of definitions on the topic of circles provided by Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as radius, diameter, circumference, chord, and tangent, each explained with clarity and precision. Understanding these fundamental concepts is crucial for students as they form the building blocks for more advanced studies in geometry and algebra.	Definition of a Circle
Math Definitions Collection: Circles	Overview The collection of definitions on the topic of circles provided by Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as radius, diameter, circumference, chord, and tangent, each explained with clarity and precision. Understanding these fundamental concepts is crucial for students as they form the building blocks for more advanced studies in geometry and algebra.	Definition of a Circle
Math Definitions Collection: Circles	Overview The collection of definitions on the topic of circles provided by Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as radius, diameter, circumference, chord, and tangent, each explained with clarity and precision. Understanding these fundamental concepts is crucial for students as they form the building blocks for more advanced studies in geometry and algebra.	Definition of a Circle
Math Definitions Collection: Circles	Overview The collection of definitions on the topic of circles provided by Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as radius, diameter, circumference, chord, and tangent, each explained with clarity and precision. Understanding these fundamental concepts is crucial for students as they form the building blocks for more advanced studies in geometry and algebra.	Definition of a Circle
Math Definitions Collection: Geometry	Overview The Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations.	Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions
Math Definitions Collection: Geometry	Overview The Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations.	Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions
Math Clip Art Collection: Geometry Concepts	Overview This collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres	Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons
Math Clip Art Collection: Geometry Concepts	Overview This collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres	Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons
Math Clip Art Collection: Geometry Concepts	Overview This collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres	Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons