
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 12: Negative Rates
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|
|
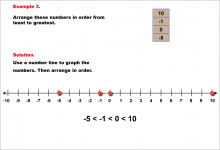
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 3 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 3
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 4 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 4
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 5 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 5
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 6 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 6
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 7 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 7
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 8 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 8
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 9 | Math Example--Rational Concepts--Comparing and Ordering Integers and Rational Numbers--Example 9
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
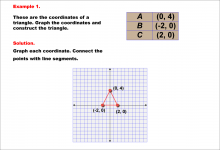
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 1 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 1
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
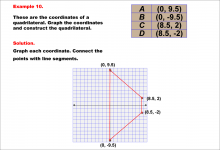
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 10 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 10
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
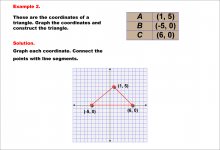
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 2 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 2
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
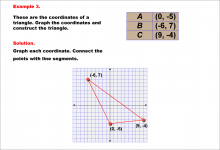
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 3 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 3
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
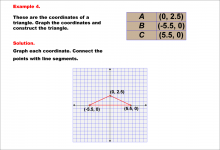
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 4 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 4
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
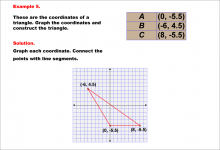
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 5 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 5
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
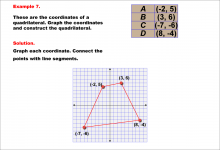
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 6 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 6
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 7 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 7
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 8 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 8
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
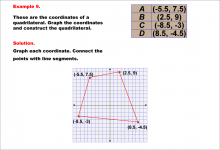
Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 9 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers on a Coordinate Grid--Example 9
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 1 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 1
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 10 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 10
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 2 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 2
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 3 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 3
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 4 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 4
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 5 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 5
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 6 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 6
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
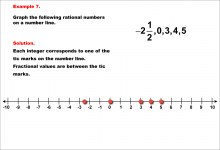
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 7 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 7
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
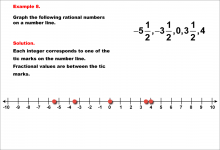
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 8 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 8
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |
|
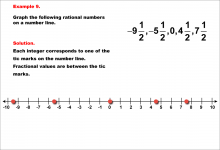
Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 9 | Math Example--Rational Concepts--Graphing Integers and Rational Numbers--Example 9
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Numerical Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 1 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 1
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 2 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 2
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 3 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 3
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 4 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 4
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 5 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 5
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 6 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 6
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 7 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 7
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 8 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 8
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 9 | Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 9
This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 1 | Math Example--Rational Concepts--Rational Expressions: Example 1TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 1/2 + 1/3. The solution involves finding a common denominator, which is 6, and then adding the fractions to get 5/6. To solve this, we multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 3/3) + (1 * 2/2) = 3/6 + 2/6. Then, we add the numerators while keeping the common denominator: (3 + 2)/6 = 5/6. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 10 | Math Example--Rational Concepts--Rational Expressions: Example 10TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 1/(8x) - 1/(3x). The solution involves finding a common denominator, which is 24x, and then subtracting the fractions to get -5/(24x). We multiply each fraction by the appropriate unit fraction to create equivalent fractions with the common denominator: (1 * 3)/(8x * 3) - (1 * 8)/(3x * 8) = 3/(24x) - 8/(24x). Then, we subtract the numerators while keeping the common denominator: (3 - 8)/(24x) = -5/(24x). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 11 | Math Example--Rational Concepts--Rational Expressions: Example 11TopicRational Expressions DescriptionThis example illustrates how to combine the rational expressions 2/(3x) + 4/(5x). The solution involves finding a common denominator, which is 15x, and then adding the fractions to get 22/(15x). We multiply each fraction by the appropriate unit fraction to create equivalent fractions with the common denominator: (2 * 5)/(3x * 5) + (4 * 3)/(5x * 3) = 10/(15x) + 12/(15x). Then, we add the numerators while keeping the common denominator: (10 + 12)/(15x) = 22/(15x). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 12 | Math Example--Rational Concepts--Rational Expressions: Example 12TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 4/(7x) - 3/(8x). The solution involves finding a common denominator, which is 56x, and then subtracting the fractions to get 11/(56x). We multiply each fraction by the appropriate unit fraction to create equivalent fractions with the common denominator: (4 * 8)/(7x * 8) - (3 * 7)/(8x * 7) = 32/(56x) - 21/(56x). Then, we subtract the numerators while keeping the common denominator: (32 - 21)/(56x) = 11/(56x). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 13 | Math Example--Rational Concepts--Rational Expressions: Example 13TopicRational Expressions DescriptionThis example illustrates how to combine the rational expressions 1/(x + 1) + 1/3. The solution involves finding a common denominator, which is 3(x + 1), and then adding the fractions to get (x + 4)/(3(x + 1)). We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 3)/(x + 1) * 3 + (1 * (x + 1))/(3 * (x + 1)) = 3/(3(x + 1)) + (x + 1)/(3(x + 1)). Then, we add the numerators while keeping the common denominator: (3 + x + 1)/(3(x + 1)) = (x + 4)/(3(x + 1)). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 14 | Math Example--Rational Concepts--Rational Expressions: Example 14TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 1/(x + 3) - 1/4. The solution involves finding a common denominator, which is 4(x + 3), and then subtracting the fractions to get (-x + 1)/(4(x + 3)). We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 4)/(x + 3) * 4 - (1 * (x + 3))/(4 * (x + 3)) = 4/(4(x + 3)) - (x + 3)/(4(x + 3)). Then, we subtract the numerators while keeping the common denominator: (4 - (x + 3))/(4(x + 3)) = (-x + 1)/(4(x + 3)). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 15 | Math Example--Rational Concepts--Rational Expressions: Example 15TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 1 / (x - 5) + 1 / 6. The solution involves finding a common denominator, which is 6(x - 5), and then adding the fractions to get (x + 1) / (6(x - 5)). We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 6) / ((x - 5) * 6) + (1 * (x - 5)) / (6 * (x - 5)) = 6 / (6(x - 5)) + (x - 5) / (6(x - 5)). Then, we add the numerators while keeping the common denominator: (6 + x - 5) / (6(x - 5)) = (x + 1) / (6(x - 5)). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 16 | Math Example--Rational Concepts--Rational Expressions: Example 16TopicRational Expressions DescriptionThis example illustrates how to combine the rational expressions 1 / (x - 7) + 1 / 8. The solution involves finding a common denominator, which is 8(x - 7), and then adding the fractions to get (x + 1) / (8(x - 7)). We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 8) / ((x - 7) * 8) + (1 * (x - 7)) / (8 * (x - 7)) = 8 / (8(x - 7)) + (x - 7) / (8(x - 7)). Then, we add the numerators while keeping the common denominator: (8 + x - 7) / (8(x - 7)) = (x + 1) / (8(x - 7)). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 17 | Math Example--Rational Concepts--Rational Expressions: Example 17TopicRational Expressions DescriptionThis example demonstrates how to combine the rational expressions 1 / (x - 9) - 1 / 10. The solution involves finding a common denominator, which is 10(x - 9), and then subtracting the fractions to get (-x + 19) / (10(x - 9)). We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 10) / ((x - 9) * 10) - (1 * (x - 9)) / (10 * (x - 9)) = 10 / (10(x - 9)) - (x - 9) / (10(x - 9)). Then, we subtract the numerators while keeping the common denominator: (10 - (x - 9)) / (10(x - 9)) = (19 - x) / (10(x - 9)) = (-x + 19) / (10(x - 9)). |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 18 | Math Example--Rational Concepts--Rational Expressions: Example 18TopicRational Expressions |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 19 | Math Example--Rational Concepts--Rational Expressions: Example 19TopicRational Expressions |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 2 | Math Example--Rational Concepts--Rational Expressions: Example 2TopicRational Expressions DescriptionThis example illustrates how to combine the rational expressions 1/4 - 1/5. The solution involves finding a common denominator, which is 20, and then subtracting the fractions to get 1/20. We multiply each fraction by the appropriate factor to create equivalent fractions with the common denominator: (1 * 5/5) - (1 * 4/4) = 5/20 - 4/20. Then, we subtract the numerators while keeping the common denominator: (5 - 4)/20 = 1/20. |
Rational Expressions |

|
Math Example--Rational Concepts--Rational Expressions: Example 20 | Math Example--Rational Concepts--Rational Expressions: Example 20TopicRational Expressions |
Rational Expressions |