
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 12: Negative Rates
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
Math Example--Ratios and Rates--Example 32 | Math Example--Ratios and Rates--Example 32TopicRatios and Rates DescriptionThis example explores temperature unit conversion, specifically converting Fahrenheit to Celsius for the freezing point of water. The image shows icicles, providing a visual representation of the freezing temperature for the mathematical problem. |
Ratios and Rates |
|
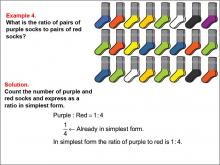
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
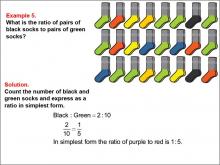
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
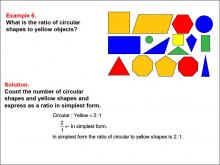
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
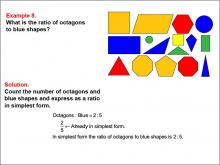
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
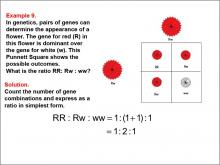
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 1 | Ratios with Fractions--Example 1TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 10 | +Ratios with Fractions--Example 10TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 11 | Ratios with Fractions--Example 11TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 2 | Ratios with Fractions--Example 2TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 3 | Ratios with Fractions--Example 3TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 4 | Ratios with Fractions--Example 4TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 5 | Ratios with Fractions--Example 5TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 6 | Ratios with Fractions--Example 6TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 7 | Ratios with Fractions--Example 7TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 8 | Ratios with Fractions--Example 8TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Ratios with Fractions--Example 9 | Ratios with Fractions--Example 9TopicRatios and Fractions DescriptionIn many scenarios, ratios are expressed using whole numbers, yet there are instances, like in recipes, where fractions play a significant role. This example illustrates a ratio involving fractions and demonstrates how to convert it into a ratio with whole numbers. Students will engage in understanding the process of converting these fractions to whole numbers, enhancing their comprehension of ratios and their practical applications such as cooking or mixing. The focus is on the fundamental skill of fraction conversion and applying it in a ratio context. |
Ratios and Rates |
|
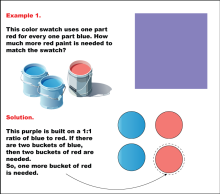
Math Example: Color Mixtures: Example 1 | Math Example: Color Mixtures: Example 1TopicRatios DescriptionThis example demonstrates a color mixture using a 1:1 ratio of red to blue paint to create purple. The image shows a purple color swatch and illustrates that for every one part of blue paint, one part of red paint is needed. In this specific case, there are two buckets of blue paint, so two buckets of red paint are required to maintain the 1:1 ratio. One additional bucket of red paint is needed to achieve the desired mixture. |
Ratios and Rates |
|
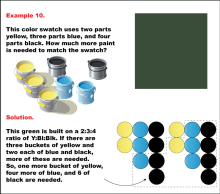
Math Example: Color Mixtures: Example 10 | Math Example: Color Mixtures: Example 10TopicRatios DescriptionThis example features a dark green color swatch created using a 2:3:4 ratio of yellow, blue, and black paint. The problem presents three buckets of yellow and two each of blue and black paint, asking students to calculate the additional paint needed to match the swatch. The solution requires adding one more bucket of yellow, four more of blue, and six more of black to achieve the correct proportions. |
Ratios and Rates |
|
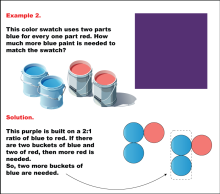
Math Example: Color Mixtures: Example 2 | Math Example: Color Mixtures: Example 2TopicRatios DescriptionThis example illustrates a color mixture using a 2:1 ratio of blue to red paint to create a specific shade of purple. The image displays a purple color swatch and shows that for every two parts of blue paint, one part of red paint is needed. In this scenario, there are two buckets each of blue and red paint, but to maintain the 2:1 ratio, two more buckets of blue paint are required. |
Ratios and Rates |
|
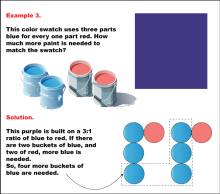
Math Example: Color Mixtures: Example 3 | Math Example: Color Mixtures: Example 3TopicRatios DescriptionThis example demonstrates a color mixture using a 3:1 ratio of blue to red paint to create a specific shade of purple. The image shows a purple color swatch and illustrates that for every three parts of blue paint, one part of red paint is needed. In this case, there are two buckets each of blue and red paint, but to maintain the 3:1 ratio, four more buckets of blue paint are required. |
Ratios and Rates |

|
Math Example: Color Mixtures: Example 4 | Math Example: Color Mixtures: Example 4TopicRatios DescriptionThis example illustrates a color mixture using a 3:2 ratio of blue to red paint to create a specific shade of purple. The image displays a purple color swatch and shows that for every three parts of blue paint, two parts of red paint are needed. In this scenario, there are two buckets each of blue and red paint, but to maintain the 3:2 ratio, four more buckets of blue paint and one more bucket of red paint are required. |
Ratios and Rates |
|
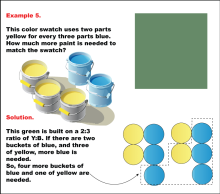
Math Example: Color Mixtures: Example 5 | Math Example: Color Mixtures: Example 5TopicRatios DescriptionThis example demonstrates a color mixture using a 2:3 ratio of yellow to blue paint to create a specific shade of green. The image shows a green color swatch and illustrates that for every two parts of yellow paint, three parts of blue paint are needed. In this case, there are three buckets of yellow paint and two buckets of blue paint, but to maintain the 2:3 ratio, one more bucket of yellow paint and four more buckets of blue paint are required. |
Ratios and Rates |
|
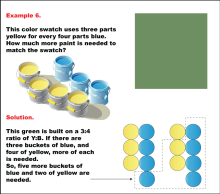
Math Example: Color Mixtures: Example 6 | Math Example: Color Mixtures: Example 6TopicRatios DescriptionThis color swatch demonstrates a green hue created by mixing three parts yellow for every four parts blue. The example illustrates how to determine the amount of additional paint needed to match the swatch when given an initial quantity. In this case, with three buckets of blue and four of yellow available, five more buckets of blue and two more of yellow are required to achieve the correct 3:4 ratio. |
Ratios and Rates |
|
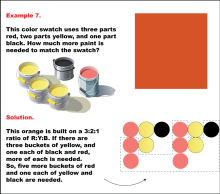
Math Example: Color Mixtures: Example 7 | Math Example: Color Mixtures: Example 7TopicRatios DescriptionThis example showcases an orange color swatch created using a 3:2:1 ratio of red, yellow, and black paint. The problem presents three buckets of yellow, one bucket of red, and one bucket of black paint, asking students to determine how much additional paint is needed to match the swatch. The solution requires adding five more buckets of red and one each of yellow and black to achieve the correct proportions. |
Ratios and Rates |
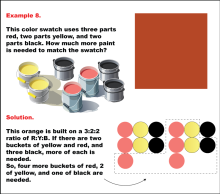
|
Math Example: Color Mixtures: Example 8 | Math Example: Color Mixtures: Example 8TopicRatios DescriptionThis example features an orange color swatch created using a 3:2:2 ratio of red, yellow, and black paint. The problem presents two buckets each of yellow and red paint, and three buckets of black paint. Students are asked to calculate the additional paint needed to match the swatch. The solution requires adding four more buckets of red, two of yellow, and one of black to achieve the correct proportions. |
Ratios and Rates |
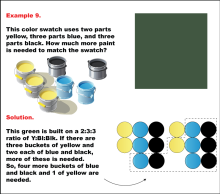
|
Math Example: Color Mixtures: Example 9 | Math Example: Color Mixtures: Example 9TopicRatios DescriptionThis example showcases a dark green color swatch created using a 2:3:3 ratio of yellow, blue, and black paint. The problem presents three buckets of yellow and two each of blue and black paint, challenging students to determine the additional paint needed to match the swatch. The solution requires adding four more buckets each of blue and black, and one more of yellow to achieve the correct proportions. |
Ratios and Rates |
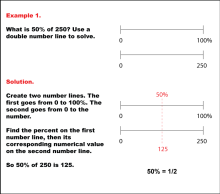
|
Math Example: Percents with Double Number Lines: Example 1 | Math Example: Percents with Double Number Lines: Example 1TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 50% of 250 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 250. By aligning 50% on the percentage line with its corresponding value on the numerical line, we can see that 50% of 250 is 125. This method visually represents the concept that 50% is equivalent to one-half of a quantity. |
Ratios and Rates |
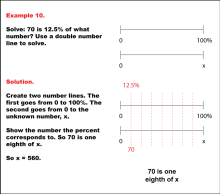
|
Math Example: Percents with Double Number Lines: Example 10 | Math Example: Percents with Double Number Lines: Example 10TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine an unknown value using a double number line when given a part and its corresponding percentage, involving a decimal percentage. The image shows two number lines: one ranging from 0 to 100% and another from 0 to an unknown number x. The position 70 is marked on the second line, visually illustrating the process of finding x when 70 is 12.5% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 11 | Math Example: Percents with Double Number Lines: Example 11TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 75, with 25 marked as an intermediate point. This visual representation helps students understand the relationship between the part (25) and the whole (75) in percentage terms. |
Ratios and Rates |
|
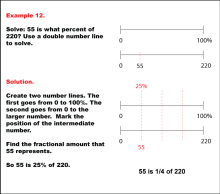
Math Example: Percents with Double Number Lines: Example 12 | Math Example: Percents with Double Number Lines: Example 12TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 220, with 55 marked as an intermediate point. This visual representation helps students understand the relationship between the part (55) and the whole (220) in percentage terms. |
Ratios and Rates |
|
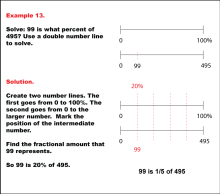
Math Example: Percents with Double Number Lines: Example 13 | Math Example: Percents with Double Number Lines: Example 13TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 495, with 99 marked as an intermediate point. This visual representation helps students understand the relationship between the part (99) and the whole (495) in percentage terms. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 14 | Math Example: Percents with Double Number Lines: Example 14TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 396, with 198 marked at the midpoint. This visual representation helps students understand the relationship between the part (198) and the whole (396) in percentage terms. |
Ratios and Rates |
|
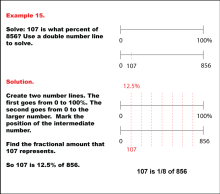
Math Example: Percents with Double Number Lines: Example 15 | Math Example: Percents with Double Number Lines: Example 15TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line, particularly when dealing with more complex ratios. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 856, with 107 marked at an eighth of the way. This visual representation helps students understand the relationship between the part (107) and the whole (856) in percentage terms. |
Ratios and Rates |
|
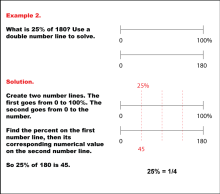
Math Example: Percents with Double Number Lines: Example 2 | Math Example: Percents with Double Number Lines: Example 2TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 25% of 180 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 180. By aligning 25% on the percentage line with its corresponding value on the numerical line, we can determine that 25% of 180 is 45. This method visually demonstrates that 25% is equivalent to one-quarter of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 3 | Math Example: Percents with Double Number Lines: Example 3TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 33 1/3% of 240 using a double number line. The solution displays two parallel number lines: one ranging from 0 to 100% and the other from 0 to 240. By aligning 33 1/3% on the percentage line with its corresponding value on the numerical line, we can see that 33 1/3% of 240 is 80. This method visually represents the concept that 33 1/3% is equivalent to one-third of a quantity. |
Ratios and Rates |
|
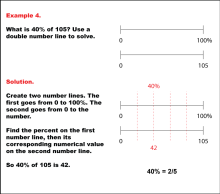
Math Example: Percents with Double Number Lines: Example 4 | Math Example: Percents with Double Number Lines: Example 4TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate 40% of 105 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 105. By aligning 40% on the percentage line with its corresponding value on the numerical line, we can determine that 40% of 105 is 42. This method visually demonstrates that 40% is equivalent to two-fifths of a quantity. |
Ratios and Rates |
|
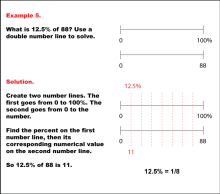
Math Example: Percents with Double Number Lines: Example 5 | Math Example: Percents with Double Number Lines: Example 5TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 12.5% of 88 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 88. By aligning 12.5% on the percentage line with its corresponding value on the numerical line, we can see that 12.5% of 88 is 11. This method visually represents the concept that 12.5% is equivalent to one-eighth of a quantity. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 6 | Math Example: Percents with Double Number Lines: Example 6TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to solve for an unknown value using a double number line when given a percentage. The image features two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 75 is 50% of x. |
Ratios and Rates |
|
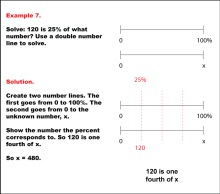
Math Example: Percents with Double Number Lines: Example 7 | Math Example: Percents with Double Number Lines: Example 7TopicRatios, Proportions, Percents DescriptionThis example illustrates how to determine an unknown value using a double number line when given a part and its corresponding percentage. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to an unknown value x. It visually demonstrates the process of finding x when 120 is 25% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 8 | Math Example: Percents with Double Number Lines: Example 8TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find an unknown value using a double number line when given a part and its corresponding percentage, involving a fractional percentage. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 125 is 33 1/3% of x. |
Ratios and Rates |
|
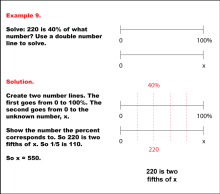
Math Example: Percents with Double Number Lines: Example 9 | Math Example: Percents with Double Number Lines: Example 9TopicRatios, Proportions, Percents DescriptionThis example illustrates how to solve for an unknown value using a double number line when given a part and its corresponding percentage. The image shows two horizontal number lines: the top line ranges from 0 to 100%, and the bottom line ranges from 0 to an unknown number x. The 40% mark on the top line aligns with 220 on the bottom line, visually demonstrating the process of finding x when 220 is 40% of x. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 1 | Math Example: Ratios with Double Number Lines: Example 1TopicRatios DescriptionThis example demonstrates the use of double number lines to solve a ratio problem involving orange and lemon juice. The juice mixture uses a ratio of 2 parts orange juice to 1 part lemon juice. Given 6 cups of orange juice, students are asked to determine the amount of lemon juice needed. The solution involves aligning the double number lines at the amount of orange juice and reading the corresponding amount of lemon juice, which is 3 cups. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 10 | Math Example: Ratios with Double Number Lines: Example 10TopicRatios DescriptionThis example introduces a four-part ratio of 5:2:1:1 for orange, lemon, lime, and strawberry juice. Given 10 cups of orange juice, students need to determine the amounts of lemon, lime, and strawberry juice required. The solution shows that 4 cups of lemon juice and 2 cups each of lime and strawberry juice are needed to maintain the ratio. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 2 | Math Example: Ratios with Double Number Lines: Example 2TopicRatios DescriptionThis example builds upon the previous one, using the same ratio of 2 parts orange juice to 1 part lemon juice. However, in this case, students are given 4 cups of lemon juice and asked to determine the amount of orange juice needed. The solution involves aligning the double number lines at the amount of lemon juice and reading the corresponding amount of orange juice, which is 8 cups. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 3 | Math Example: Ratios with Double Number Lines: Example 3TopicRatios DescriptionThis example introduces a new ratio of 3 parts orange juice to 1 part lime juice. Students are given 9 cups of orange juice and asked to determine the amount of lime juice needed. The solution involves using a double number line to align at the amount of orange juice and find the corresponding amount of lime juice, which is 3 cups. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 4 | Math Example: Ratios with Double Number Lines: Example 4TopicRatios DescriptionThis example introduces a more complex ratio of 3 parts orange juice to 2 parts lime juice. Students are given 4 cups of lime juice and asked to determine the amount of orange juice needed. The solution involves using a double number line to align at the amount of lime juice and find the corresponding amount of orange juice, which is 6 cups. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 5 | Math Example: Ratios with Double Number Lines: Example 5TopicRatios DescriptionThis example introduces a three-part ratio of 2:1:1 for orange, lemon, and raspberry juice. Given 4 cups of orange juice, students need to determine the amounts of lemon and raspberry juice required. The solution shows that 2 cups each of lemon and raspberry juice are needed to maintain the ratio. |
Ratios and Rates |

|
Math Example: Ratios with Double Number Lines: Example 6 | Math Example: Ratios with Double Number Lines: Example 6TopicRatios DescriptionThis example presents a three-part ratio of 3:2:2 for orange, lemon, and raspberry juice. Given 6 cups of lemon juice, students need to determine the amounts of orange and raspberry juice required. The solution shows that 9 cups of orange juice and 6 cups of raspberry juice are needed to maintain the ratio. |
Ratios and Rates |