
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 10: Different Options for Solving One Equation
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |
|
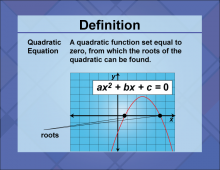
Definition--Quadratics Concepts--Quadratic Equation | Quadratic EquationTopicQuadratics Concepts DefinitionA quadratic equation is a polynomial equation of degree two, typically in the form ax2 + bx + c = 0 where a, b, and c are constants and a ≠ 0. |
Quadratic Equations and Functions |

|
Definition--Rationals and Radicals--Radical Equations | Radical EquationsTopicRationals and Radicals DefinitionRadical equations are equations in which the variable is inside a radical, such as a square root or cube root. DescriptionRadical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve √x+3=5 one would square both sides to obtain x+3=25 |
Radical Functions and Equations |

|
Definition--Rationals and Radicals--Rational Equations | Rational EquationsTopicRationals and Radicals DefinitionRational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator. DescriptionRational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve 1x+1x+1=12 |
Rational Functions and Equations |
|
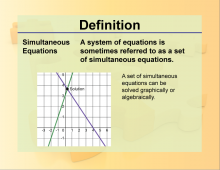
Definition--Systems Concepts--Simultaneous Equations | Definition--Systems Concepts--Simultaneous Equations
This is part of a collection of definitions related to the topic of systems of equations. The focus of most of the terms is linear systems. |
Solving Systems of Equations |

|
Desmos Activity: Equations of Parabolas 1 | Derive the equation of a parabola with a vertex at the origin and focus at coordinates (0, f) using a Desmos graphing calculator. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file.
Related ResourcesTo see additional resources on this topic click on the Related Resources tab above.Desmos CollectionTo see the complete collection of Desmos Resources click on this link. |
Graphs of Quadratic Functions |

|
Desmos Activity: Equations of Parabolas 2 | Derive the equation of a parabola with Focus at coordinates (a, c) and Directrix at y = c using a Desmos graphing calculator. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link. |
Graphs of Quadratic Functions |

|
Desmos Activity: Linear Equations in Point-Slope Form | In this graphing calculator activity, have your students explore how to convert linear equations in point-slope to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of coordinates of the point and the slope of the line. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link. |
Point-Slope Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Elementary Definition--Multiplication and Division Concepts--False Equation | False EquationTopicMultiplication and Division DefinitionA false equation is a mathematical statement that shows equality between two expressions that are not equal. |
Multiplication Expressions and Equations |

|
Elementary Definition--Multiplication and Division Concepts--True Equation | True EquationTopicMultiplication and Division DefinitionA true equation is a mathematical statement that asserts equality between two expressions that are equal. DescriptionTrue equations are essential in mathematics as they represent accurate relationships between numbers and expressions. For example, the equation 2 + 3 = 5 |
Multiplication Expressions and Equations |

|
Elementary Math Definitions--Addition Subtraction Concepts--False Equation | False EquationTopicAddition and Subtraction DefinitionA false equation is a mathematical statement that shows two expressions that are not equal. DescriptionA false equation is a mathematical statement where two expressions are not equal. For example, the equation 3 + 4 = 8 is false because the sum of 3 and 4 is 7, not 8. Understanding false equations helps students recognize and correct errors in their calculations. |
Addition Expressions and Equations |

|
Elementary Math Definitions--Addition Subtraction Concepts--True Equation | True EquationTopicAddition and Subtraction DefinitionA true equation is a mathematical statement that shows two expressions that are equal. DescriptionA true equation is a mathematical statement where two expressions are equal. For example, the equation 3 + 4 = 7 is true because the sum of 3 and 4 is indeed 7. Understanding true equations helps students recognize and verify the accuracy of their calculations. |
Addition Expressions and Equations |

|
Equations Word Search Puzzle 2 | Equations Word Search Puzzle 2
Review key vocabulary on the topic of equations with this interactive and printable word search puzzle. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Applications of Equations and Inequalities, Solving One-Step Equations and Solving Two-Step Equations |

|
Instructional Resource--Strategy Pack--One-Step Addition Equations | Instructional Resource | Strategy Pack | One-Step Addition Equations
Learn different strategies for solving one-step addition equations. The Strategy Packs provide alternate ways of solving the same problem, giving your students different approaches to the same problem. The goal of the Strategy Packs is to encourage your students to think strategically when solving math problems. —PRESS PREVIEW TO LAUNCH THE PRESENTATION— To see the complete collection of Instructional Resources, click on this link.Note: The download is a PPT file. |
Solving One-Step Equations |

|
Instructional Resource--Strategy Pack--One-Step Multiplication Equations | Instructional Resource | Strategy Pack | One-Step Multiplication Equations
Learn different strategies for solving one-step multiplication equations. The Strategy Packs provide alternate ways of solving the same problem, giving your students different approaches to the same problem. The goal of the Strategy Packs is to encourage your students to think strategically when solving math problems. —PRESS PREVIEW TO LAUNCH THE PRESENTATION— To see the complete collection of Instructional Resources, click on this link.Note: The download is a PPT file. |
Solving One-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + -b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: AX + By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax - b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax - b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax - b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax - b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |