Illustrative Math Alignment: Grade 7 Unit 7

Expressions, Equations, and Inequalities

Lesson 19: Expanding and Factoring

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Math Example--Combinatorics--Factorial Expressions: Example 8	Math Example--Combinatorics--Factorial Expressions: Example 8 This is part of a collection of math examples that focus on combinatorics and factorial expressions.	Combinatorics
Math Example--Combinatorics--Factorial Expressions: Example 9	Math Example--Combinatorics--Factorial Expressions: Example 9 This is part of a collection of math examples that focus on combinatorics and factorial expressions.	Combinatorics
Math Example--Quadratics--Factoring Quadratics: Example 1	Factoring Quadratics: Example 1 Topic Quadratics Description This example demonstrates the factoring of a simple quadratic expression in the form x² + bx + c. The factoring process involves finding two numbers that multiply to give c and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. Factoring is often the quickest and most straightforward method for solving quadratic equations when the coefficients are integers or simple fractions.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 10	Factoring Quadratics: Example 10 Topic Quadratics Description This example showcases factoring a quadratic expression in standard form where a = 1The factoring process involves finding two numbers that multiply to give c and add up to b, considering both positive and negative factors. For instance, if the expression is x² + 5x - 24, we would look for factors of -24 that add up to 5, resulting in (x + 8)(x - 3). This method is particularly useful for solving quadratic equations and understanding the nature of the roots. It demonstrates how the signs of the factors relate to the signs of the roots, enhancing students' ability to analyze quadratic functions both algebraically and graphically.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 11	Factoring Quadratics: Example 11 Topic Quadratics Description This example illustrates factoring a quadratic expression in standard form where b = 0. The factoring process remains the same: finding two numbers that multiply to give c and add up to b, but in this case they add up to 0. For example, if the expression is x² - 13x + 36, we would look for factors of 36 that add up to -13, resulting in (x - 9)(x - 4). This type of example helps students develop their factoring skills with more challenging numbers, preparing them for more complex problem-solving scenarios. It reinforces the importance of considering both positive and negative factors and strengthens algebraic manipulation skills.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 2	Factoring Quadratics: Example 2 Topic Quadratics Description This example shows the factoring of a quadratic expression of the form x2 + bx + c, which is a modified version of the standard form. This type of factoring involves finding the factors of c that also add up to b. This skill is essential for solving more complex quadratic equations and understanding the structure of quadratic expressions. It helps in identifying the roots of quadratic functions that are not in standard form, which is crucial in many applications in physics and engineering where quadratic relationships are common.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 3	Factoring Quadratics: Example 2 Topic Quadratics Description This example shows the factoring of a quadratic expression in standard form, where a = 1. This type of factoring often involves finding the factors of a•c that add up to b. This skill is essential for solving more complex quadratic equations and understanding the structure of quadratic expressions. It helps in identifying the roots of quadratic functions that are not in standard form, which is crucial in many applications in physics and engineering where quadratic relationships are common.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 4	Factoring Quadratics: Example 4 Topic Quadratics Description This example shows the factoring of a quadratic expression in standard form (ax² + bx + c), where a = 1. The factoring process involves finding two numbers that multiply to give a•c (which is simply c in this case) and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. This type of factoring is often the first step in solving quadratic equations and is essential for understanding the structure of quadratic expressions.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 5	Factoring Quadratics: Example 4 Topic Quadratics Description This example shows the factoring of a quadratic expression in standard form (ax² + bx + c), where a = 1. The factoring process involves finding two numbers that multiply to give a•c (which is simply c in this case) and add up to b. This method is crucial for solving quadratic equations as it allows us to find the roots (or zeros) of the quadratic function. By setting each factor to zero, we can quickly determine the x-intercepts of the parabola. This type of factoring is often the first step in solving quadratic equations and is essential for understanding the structure of quadratic expressions.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 6	Factoring Quadratics: Example 6 Topic Quadratics	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 7	Factoring Quadratics: Example 7 Topic Quadratics Description This example demonstrates factoring a quadratic expression in standard form where a ≠ 1, but with a negative middle term. The process still involves finding two numbers that multiply to give a•c and add up to b, but now considering negative factors. For example, if the expression is x² - x - 12, we look for factors of -12 that add up to -1, resulting in (x - 4)(x + 3). This skill is essential for solving a wide range of quadratic equations and understanding the relationship between a quadratic's factors and its roots. It also helps in visualizing how the factored form relates to the graph of the parabola, particularly its x-intercepts.	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 8	Factoring Quadratics: Example 8 Topic Quadratics	Factoring Quadratics
Math Example--Quadratics--Factoring Quadratics: Example 9	Factoring Quadratics: Example 9 Topic Quadratics Description This example demonstrates factoring a quadratic expression where in standard form where a = 1. The process still involves finding two numbers that multiply to give c and add up to b. For example, if the expression is x² - x - 12, we look for factors of -12 that add up to -1, resulting in (x - 4)(x + 3). This skill is essential for solving a wide range of quadratic equations and understanding the relationship between a quadratic's factors and its roots. It also helps in visualizing how the factored form relates to the graph of the parabola, particularly its x-intercepts.	Factoring Quadratics
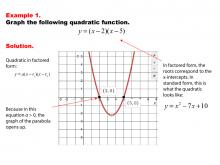
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 1	Graphs of Quadratic Functions in Factored Form--Example 1 Topic Quadratics	Graphs of Quadratic Functions
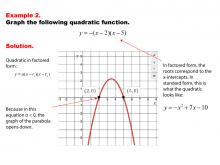
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 2	Graphs of Quadratic Functions in Factored Form--Example 2 Topic Quadratics Description In this example, the quadratic function is presented in factored form, highlighting its roots and facilitating the graphing process. Unlike the standard form, the factored form provides immediate insight into the x-intercepts of the graph, allowing for a quick and accurate sketch of the parabola. This form is particularly useful for visualizing the solutions of the equation and understanding the function's behavior.	Graphs of Quadratic Functions
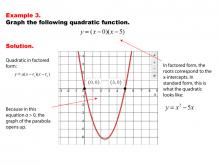
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 3	Graphs of Quadratic Functions in Factored Form--Example 3 Topic Quadratics Description This example demonstrates the graphing of a quadratic function in factored form. The factored form is advantageous because it clearly indicates where the graph will intersect the x-axis, making it easier to plot the parabola accurately. This form simplifies the process of identifying the roots and understanding the quadratic's graphical representation.	Graphs of Quadratic Functions
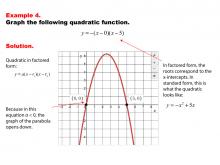
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 4	Graphs of Quadratic Functions in Factored Form--Example 4 Topic Quadratics Description The factored form of this quadratic function allows for easy identification of the roots, which are the x-intercepts of the graph. This form is different from the standard form in that it directly provides the points where the parabola crosses the x-axis, simplifying the graphing process. This example illustrates how the factored form can be used to quickly and effectively graph a quadratic function.	Graphs of Quadratic Functions
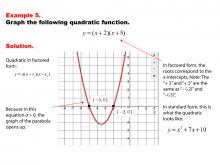
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 5	Graphs of Quadratic Functions in Factored Form--Example 5 Topic Quadratics Description This example highlights the advantages of using the factored form for graphing quadratic functions. The factored form makes it straightforward to determine the roots, which are the x-intercepts of the graph. This simplifies the process of plotting the parabola and understanding the function's behavior, as the roots are immediately visible and can be used to sketch the graph accurately.	Graphs of Quadratic Functions
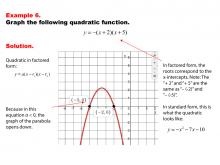
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 6	Graphs of Quadratic Functions in Factored Form--Example 6 Topic Quadratics Description The factored form of a quadratic function provides a clear and efficient way to graph the function by identifying the roots directly. This example shows how the factored form differs from the standard form by offering immediate insight into the x-intercepts, simplifying the graphing process and enhancing understanding of the function's graphical representation.	Graphs of Quadratic Functions
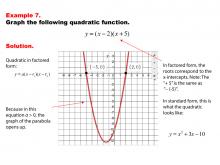
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 7	Graphs of Quadratic Functions in Factored Form--Example 7 Topic Quadratics Description In this example, the quadratic function is expressed in factored form, which simplifies the process of graphing by providing the roots directly. This form contrasts with the standard form, where additional calculations are needed to find the roots. The factored form allows for a more straightforward and intuitive graphing process, as it clearly indicates the x-intercepts of the parabola.	Graphs of Quadratic Functions
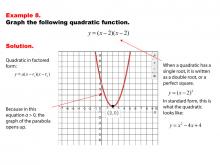
Math Example--Quadratics--Graphs of Quadratic Functions in Factored Form--Example 8	Graphs of Quadratic Functions in Factored Form--Example 8 Topic Quadratics Description This example illustrates the benefits of using the factored form for graphing quadratic functions. The factored form provides immediate information about the roots, making it easier to sketch the parabola by pinpointing the x-intercepts. This form is a simpler alternative to the standard form when graphing, as it eliminates the need for additional calculations to determine the roots.	Graphs of Quadratic Functions
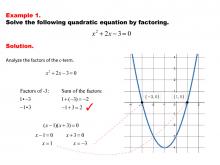
Math Example--Quadratics--Solving Quadratics by Factoring--Example 1	Solving Quadratics by Factoring--Example 1 Topic Quadratics Description Factoring is a technique used to solve quadratic equations by expressing them as a product of binomials. Once in factored form, finding the roots of the quadratic becomes straightforward as it involves setting each binomial equal to zero. In this example, the quadratic equation is factored into two binomials, allowing for easy identification of the roots. The graphic illustrates the step-by-step process of factoring and solving, highlighting the efficiency of this method for certain types of quadratic equations.	Quadratic Equations and Functions
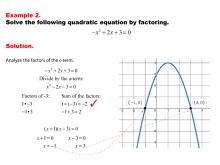
Math Example--Quadratics--Solving Quadratics by Factoring--Example 2	Solving Quadratics by Factoring--Example 2 Topic Quadratics Description This example demonstrates solving a quadratic equation by factoring. The equation is rewritten as a product of binomials, simplifying the process of finding the roots. The graphic shows how each binomial is set to zero to find the solutions, illustrating the straightforward nature of this method when applicable. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
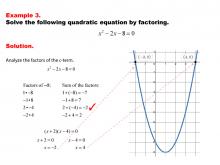
Math Example--Quadratics--Solving Quadratics by Factoring--Example 3	Solving Quadratics by Factoring--Example 3 Topic Quadratics Description In this example, the quadratic equation is solved by factoring, which involves expressing the equation as a product of binomials. The process makes it easy to find the roots by setting each factor equal to zero. The graphic provides a detailed walkthrough of the factoring steps, showcasing the simplicity and effectiveness of this approach for solving quadratics. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
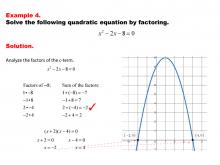
Math Example--Quadratics--Solving Quadratics by Factoring--Example 4	Solving Quadratics by Factoring--Example 4 Topic Quadratics Description This example illustrates the process of solving a quadratic equation by factoring. The equation is factored into binomials, and the roots are found by setting each binomial to zero. The graphic highlights the steps involved in factoring and solving, emphasizing the method's efficiency for certain quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
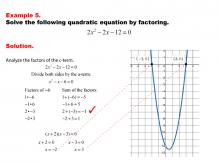
Math Example--Quadratics--Solving Quadratics by Factoring--Example 5	Solving Quadratics by Factoring--Example 5 Topic Quadratics Description In this example, the quadratic equation is solved by factoring, a method that involves rewriting the equation as a product of binomials. This approach simplifies finding the roots, as each binomial is set to zero to solve for the variable. The graphic provides a step-by-step guide to the factoring process, demonstrating its practicality and ease of use. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
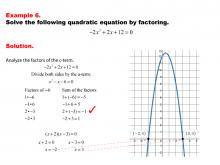
Math Example--Quadratics--Solving Quadratics by Factoring--Example 6	Solving Quadratics by Factoring--Example 6 Topic Quadratics Description This example demonstrates solving a quadratic equation by factoring. The equation is expressed as a product of binomials, allowing for straightforward determination of the roots by setting each factor to zero. The graphic illustrates the factoring process, highlighting its effectiveness for solving quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
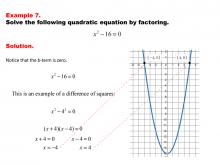
Math Example--Quadratics--Solving Quadratics by Factoring--Example 7	Solving Quadratics by Factoring--Example 7 Topic Quadratics Description In this example, the quadratic equation is solved by factoring, which involves expressing it as a product of binomials. This method simplifies finding the roots, as each binomial is set to zero. The graphic provides a clear demonstration of the factoring process, showcasing its simplicity and utility in solving quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
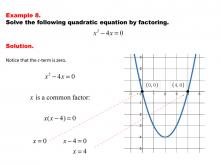
Math Example--Quadratics--Solving Quadratics by Factoring--Example 8	Solving Quadratics by Factoring--Example 8 Topic Quadratics Description This example illustrates solving a quadratic equation by factoring. The equation is rewritten as a product of binomials, and the roots are found by setting each factor to zero. The graphic highlights the steps involved in factoring and solving, emphasizing the method's efficiency and applicability to certain quadratic equations. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Equations and Functions
MATH EXAMPLES--Teacher's Guide: Factoring Quadratics	MATH EXAMPLES--Teacher's Guide: Factoring Quadratics This Teacher's Guide provides an overview of the 11 worked-out examples that show how to factor quadratic expressions. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Polynomial Expressions
Math Video Definition 20--Multiplication and Division Concepts--Factor	Math Video Definition 20--Multiplication and Division Concepts--Factor This is part of a collection of math video definitions related to the topics of Multiplication and Division, ideal for use in an early elementary classroom. Note: The download is an MP4 video.	Multiplication Expressions and Equations
Math Video Definition 22--Multiplication and Division Concepts--Greatest Common Factor (GCF)	Math Video Definition 22--Multiplication and Division Concepts--Greatest Common Factor (GCF) This is part of a collection of math video definitions related to the topics of Multiplication and Division, ideal for use in an early elementary classroom. Note: The download is an MP4 video.	Multiplication Expressions and Equations
Math Video Definition 44--Multiplication and Division Concepts--Prime Factorization	Math Video Definition 44--Multiplication and Division Concepts--Prime Factorization This is part of a collection of math video definitions related to the topics of Multiplication and Division, ideal for use in an early elementary classroom. Note: The download is an MP4 video.	Multiplication Expressions and Equations
Paper-and-Pencil Quiz: Factoring Quadratics (Easy)	Paper-and-Pencil Quiz: Factoring Quadratics (Easy) This is part of a collection of math quizzes on the topic of Factoring Quadratics. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key). Related Resources To see additional resources on this topic, click on the Related Resources tab. Quiz Library To see the complete collection of Quizzes, click on this link. ary">click on this link.	Factoring Quadratics
Paper-and-Pencil Quiz: Factoring Quadratics (Hard)	Paper-and-Pencil Quiz: Factoring Quadratics (Hard) This is part of a collection of math quizzes on the topic of Factoring Quadratics. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key). Related Resources To see additional resources on this topic, click on the Related Resources tab. Quiz Library To see the complete collection of Quizzes, click on this link. ary">click on this link.	Factoring Quadratics
Paper-and-Pencil Quiz: Factoring Quadratics (Medium)	Paper-and-Pencil Quiz: Factoring Quadratics (Medium) This is part of a collection of math quizzes on the topic of Factoring Quadratics. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key). Related Resources To see additional resources on this topic, click on the Related Resources tab. Quiz Library To see the complete collection of Quizzes, click on this link. ary">click on this link.	Factoring Quadratics
Quizlet Flash Card Set: Factoring Polynomials	Description In this set of interactive flash cards students practice factoring quadratic polynomials. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Factoring Polynomials
Quizlet Flash Cards: Adding Rational Numbers, Set 01	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 02	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 03	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 04	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 05	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 06	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 07	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 08	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 09	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Rational Numbers, Set 10	Description Add rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Numerical Expressions
Quizlet Flash Cards: Adding Variable Expressions, Set 01	Description Add variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Variable Expressions
Quizlet Flash Cards: Adding Variable Expressions, Set 02	Description Add variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Variable Expressions
Quizlet Flash Cards: Adding Variable Expressions, Set 03	Description Add variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related Resources To see other resources related to this topic, click on the Resources tab above. Quizlet Library To see the complete Quizlet Flash Card Library, click on this Link to see the collection.	Variable Expressions