Illustrative Math Alignment: Grade 7 Unit 7

Topic

Volume

Description

A hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080.

Topic

Volume

Description

A hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2).

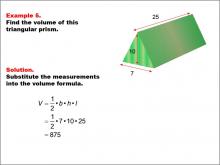
Topic

Volume

Description

The image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875.

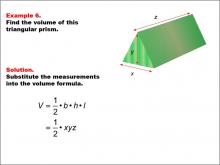
Topic

Volume

Description

The image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z..

Topic

Volume

Description

The image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525..

Topic

Volume

Description

This image shows a hollow triangular prism with outer dimensions labeled as x, y, and z, and inner dimensions reduced by 2 units each. It demonstrates how to calculate the volume by subtracting the hollow region from the full prism. This image illustrates Example 8: "Find the volume of this hollow triangular prism." The solution uses V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = z(xy - (x - 2)(y - 2)) = z(x + y - 2)..

Topic

Volume

Description

A green cylinder with a radius of 10 units and a height of 8 units. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 9: The task is to find the volume of the cylinder. The volume formula V = πr2h is used. Substituting the values r = 10 and h = 8, the volume is calculated as V= 800π.

This Teacher's Guide provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

This set of tutorials provides 24 examples of how to find the volume of various 3-dimensional geometric figures.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

This set of tutorials provides 24 examples of how to find the volume of various 3-dimensional geometric figures. NOTE: The download is a PPT file.

Topic

3D Geometry

Definition

Surface area is the total area covered by the surface of a three-dimensional object.

This is part of a collection of math video definitions related to the topic of 3D Geometry. These videos have Spanish audio. Note: The download is an MP4 video.

This is the transcript for the video of same title. Video contents: The glass-paneled pyramid at the Louvre Museum in Paris is a tessellation of rhombus-shaped glass panels. Students create a model of the pyramid to calculate the number of panels used to cover the surface area of the pyramid.

This is the transcript for the video of same title. Video contents: The Citibank Tower in New York City presents some unique design challenges. In addition it has to cope with a problem that all tall structure have to deal with: heat loss. By managing the ratio of surface area to volume, a skyscraper can effective manage heat loss.