
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 3: Nonadjacent Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Closed Captioned Video: Geometry Applications: Angles and Planes | Closed Captioned Video: Geometry Applications: Angles and PlanesTopicGeometry Basics |
Applications of Angles and Planes |

|
Closed Captioned Video: Geometry Applications: Angles and Planes, 1 | Closed Captioned Video: Geometry Applications: Angles and Planes, 1TopicGeometry Basics DescriptionExplore Geometry Concepts: This segment introduces angles and planes through the Earth's orbital ecliptic and its 23-degree tilt. It connects these geometric principles to real-world phenomena, such as seasons and Kepler's laws, laying a foundation for subsequent discussions on angles and planes. |
Applications of Angles and Planes |

|
Closed Captioned Video: Geometry Applications: Angles and Planes, 2 | Closed Captioned Video: Geometry Applications: Angles and Planes, 2TopicGeometry Basics DescriptionExplore Geometry Concepts: This segment focuses on the strategic use of angles in Himeji Castle for defense. It explains tangent lines, line-of-sight angles, and acute angle measurements, connecting these concepts to historical architecture and modern geometry tools for analysis. |
Applications of Angles and Planes |

|
Closed Captioned Video: Geometry Applications: Angles and Planes, 3 | Closed Captioned Video: Geometry Applications: Angles and Planes, 3TopicGeometry Basics DescriptionExplore Geometry Concepts: This segment delves into parallel planes, illustrated by sedimentary rock layers in fossil analysis. It shows how these concepts are used to determine the relative age of fossils and explores how tectonic activity can alter parallel planes to create geological intersections. |
Applications of Angles and Planes |

|
Closed Captioned Video: Geometry Applications: Triangles | Closed Captioned Video: Geometry Applications: TrianglesTopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 1 | Closed Captioned Video: Geometry Applications: Triangles, 1TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 2 | Closed Captioned Video: Geometry Applications: Triangles, 2TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Closed Captioned Video: Geometry Applications: Triangles, 3 | Closed Captioned Video: Geometry Applications: Triangles, 3TopicTriangles |
Definition of a Triangle and Applications of Triangles |

|
Definition--Angle Concepts--Adjacent Angles | Adjacent AnglesTopicAngles DefinitionAdjacent angles are two angles that share a common vertex and side, but do not overlap. |
Definition of an Angle |
|
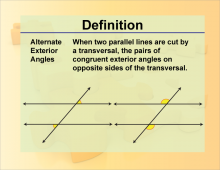
Definition--Angle Concepts--Alternate Exterior Angles | Alternate Exterior AnglesTopicAngles DefinitionAlternate exterior angles are pairs of angles formed when a transversal crosses two parallel lines, and they lie on opposite sides of the transversal and outside the parallel lines. |
Definition of an Angle |
|
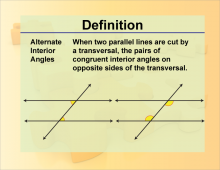
Definition--Angle Concepts--Alternate Interior Angles | Alternate Interior AnglesTopicAngles DefinitionAlternate interior angles are pairs of angles formed when a transversal crosses two parallel lines, and they lie on opposite sides of the transversal and inside the parallel lines. |
Definition of an Angle |
|
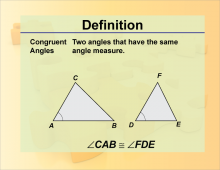
Definition--Angle Concepts--Congruent Angles | Congruent AnglesTopicAngles DefinitionCongruent angles are angles that have the same measure. DescriptionCongruent angles are a key concept in geometry, often used in proving the similarity and congruence of geometric figures. They are essential in understanding the properties of polygons, where congruent angles indicate symmetry and balance. In real-world applications, congruent angles are used in design and engineering to ensure that components are identical and fit together seamlessly. For students, learning about congruent angles enhances their understanding of geometric relationships and proofs, contributing to their overall mathematical proficiency. |
Definition of an Angle |
|
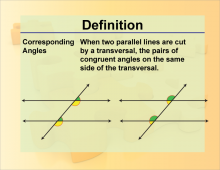
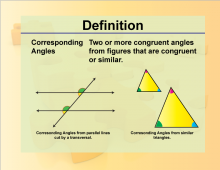
Definition--Angle Concepts--Corresponding Angles | Corresponding AnglesTopicAngles DefinitionCorresponding angles are pairs of angles that are in similar positions at each intersection where a transversal crosses two lines. |
Definition of an Angle |
|
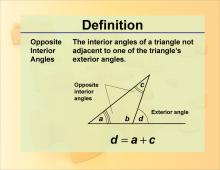
Definition--Angle Concepts--Opposite Interior Angles | Opposite Interior AnglesTopicAngles DefinitionOpposite interior angles are pairs of angles opposite the exterior angle of a triangle. In the case of parallel lines cut by a transversal, they are congruent. |
Definition of an Angle |

|
Definition--Angle Concepts--Supplementary Angles | Supplementary AnglesTopicAngles DefinitionSupplementary angles are two angles whose measures add up to 180 degrees. |
Definition of an Angle |
|
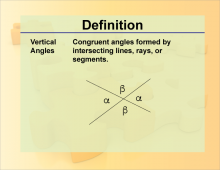
Definition--Angle Concepts--Vertical Angles | Vertical AnglesTopicAngles DefinitionVertical angles are pairs of opposite angles formed by two intersecting lines, and they are equal in measure. |
Definition of an Angle |
|
Definition--Geometry Basics--Corresponding Angles | Corresponding AnglesTopicGeometry Basics DefinitionCorresponding angles are angles that are in the same relative position at each intersection where a straight line crosses two others. DescriptionCorresponding angles are formed when a transversal intersects two parallel lines. These angles are equal in measure, which is a key concept in proving the properties of parallel lines and solving geometric problems. For example, if two parallel lines are cut by a transversal, then each pair of corresponding angles is equal. This concept is used extensively in geometry to establish relationships between angles and to solve complex problems involving parallel lines. |
Definition of an Angle |
|
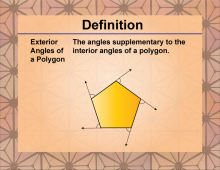
Definition--Polygon Concepts--Exterior Angles of a Polygon | Exterior Angles of a PolygonTopicPolygons DefinitionAn exterior angle of a polygon is the angle formed between any side of the polygon and the extension of an adjacent side. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Interior Angles of a Polygon | Sum of Interior Angles of a PolygonTopicPolygons DefinitionThe sum of interior angles of a polygon with n sides is given by the formula: (n - 2) × 180°, where n is the number of sides in the polygon. DescriptionThe sum of interior angles is a fundamental property of polygons that plays a crucial role in geometry. This concept is essential for understanding the structure and properties of various polygons, from simple triangles to complex multi-sided figures. The formula (n - 2) × 180° provides a quick and efficient way to calculate the total measure of all interior angles in any polygon, regardless of its regularity. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Sum of the Exterior Angles of a Polygon | Sum of Exterior Angles of a PolygonTopicPolygons DefinitionThe sum of the exterior angles of any polygon, regardless of the number of sides, is always 360°. DescriptionThe sum of exterior angles of a polygon is a fundamental concept in geometry that holds true for all polygons, regardless of their shape or number of sides. This property is crucial for understanding the nature of polygons and their relationship to circular motion. Exterior angles are formed by extending each side of the polygon and measuring the angle between this extension and the adjacent side. |
Definition of a Polygon |
|
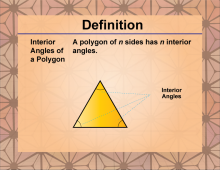
Definition--Polygon Concepts--Sum of the Interior Angles of a Polygon | Interior Angles of a PolygonTopicPolygons DefinitionAn interior angle of a polygon is an angle formed inside the polygon by two adjacent sides. |
Definition of a Polygon |
|
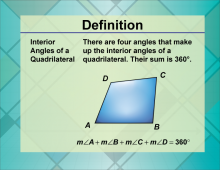
Definition--Quadrilateral Concepts--Interior Angles of a Quadrilateral | Interior Angles of a QuadrilateralTopicQuadrilaterals DefinitionThe sum of the interior angles of a quadrilateral is always 360 degrees. |
Definition of a Quadrilateral |
|
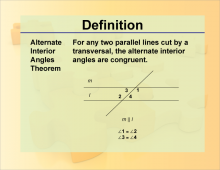
Definition--Theorems and Postulates--Alternate Interior Angles Theorem | Definition--Theorems and Postulates--Alternate Interior Angles Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of an Angle |

|
Definition--Theorems and Postulates--Converse of Same-Side Interior Angles Postulate | Definition--Theorems and Postulates--Converse of Same-Side Interior Angles Postulate
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of an Angle |

|
Definition--Theorems and Postulates--Converse of the Alternate Interior Angles Theorem | Definition--Theorems and Postulates--Converse of the Alternate Interior Angles Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of an Angle |

|
Definition--Theorems and Postulates--Converse of the Corresponding Angles Theorem | Definition--Theorems and Postulates--Converse of the Corresponding Angles Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of an Angle |

|
Definition--Theorems and Postulates--Corresponding Angles Theorem | Definition | Theorems and Postulates | Corresponding Angles Theorem
This is part of a collection of definitions of geometric theorems and postulates. —CLICK PREVIEW TO SEE THE DEFINITION— To see the complete collection of theorems and postulates, click on this link.The following section includes background information on angles. What Are Angles?In this illustration two rays intersect at a point. Points A and B are on one ray and points B and C are on another ray. These two rays form an angle. |
Definition of an Angle |
|
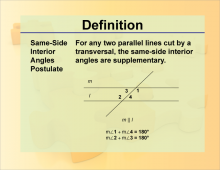
Definition--Theorems and Postulates--Same-Side Interior Angles Postulate | Definition--Theorems and Postulates--Same-Side Interior Angles Postulate
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |

|
Definition--Triangle Concepts--30-60-90 Right Triangles | 30-60-90 Right TrianglesTopicTriangles DefinitionA 30-60-90 right triangle is a right triangle with angles of 30 degrees, 60 degrees, and 90 degrees. DescriptionThe 30-60-90 triangle is a special right triangle characterized by its angle measures. The sides of this triangle are in the ratio 1:√3:2, meaning the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter leg. This relationship can be derived using trigonometric principles and is fundamental in geometry. |
Definition of a Triangle |

|
Definition--Triangle Concepts--45-45-90 Right Triangles | 45-45-90 Right TrianglesTopicTriangles DefinitionA 45-45-90 right triangle is a right triangle with two 45-degree angles and one 90-degree angle. DescriptionThe 45-45-90 triangle is another special right triangle where the two legs are of equal length, and the hypotenuse is √2 times the length of each leg. This type of triangle is also known as an isosceles right triangle due to its equal legs. |
Definition of a Triangle |
|
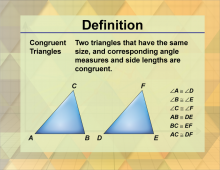
Definition--Triangle Concepts--Congruent Triangles | Congruent TrianglesTopicTriangles DefinitionCongruent triangles are triangles that have the same size and shape, with corresponding sides and angles that are equal. DescriptionCongruent triangles are fundamental in geometry, representing triangles that are identical in size and shape. This means that all corresponding sides and angles of congruent triangles are equal. The concept of congruence is crucial for proving various geometric theorems and properties. |
Definition of a Triangle |
|
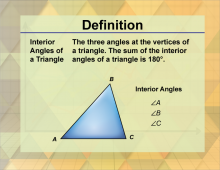
Definition--Triangle Concepts--Interior Angles of a Triangle | Interior Angles of a TriangleTopicTriangles DefinitionThe interior angles of a triangle are the angles inside the triangle, and their sum is always 180 degrees. DescriptionThe interior angles of a triangle are a fundamental concept in geometry, representing the angles inside the triangle. The sum of the interior angles of any triangle is always 180 degrees, which is a crucial property used in various geometric proofs and constructions. |
Definition of a Triangle |
|
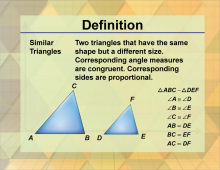
Definition--Triangle Concepts--Similar Triangles | Similar TrianglesTopicTriangles DefinitionSimilar triangles are triangles that have the same shape but not necessarily the same size, with corresponding angles equal and corresponding sides proportional. DescriptionSimilar triangles are fundamental in geometry, representing triangles that have the same shape but not necessarily the same size. This means that all corresponding angles are equal, and all corresponding sides are proportional. |
Definition of a Triangle |

|
Geometry Applications Teachers Guide: Angles and Planes | Geometry Applications Teachers Guide: Angles and Planes
This is the Teacher's Guide that accompanies Geometry Applications: Angles and Planes. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Angles and Planes |

|
Geometry Applications, Triangles, Segment 1, Introduction | VIDEO: Geometry Applications: Triangles, 1
TopicTriangles DescriptionThis video introduces the importance of triangles in architecture and structural design. It highlights the use of triangles in structures like the Bank of China Tower in Hong Kong, noting their ability to provide strength and stability. The video focuses on the role of triangles in reinforcing skyscrapers to withstand strong winds, especially during typhoon seasons. Key vocabulary includes architectural support, triangular base, and stability. The video sets up a foundation for exploring how triangle properties are applied in real-world contexts. |
Applications of Triangles and Definition of a Triangle |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Interior Angles of a Polygon | In this Slide Show, apply concepts of linear functions to the context of the interior angles of a polygon. Note: The download is a PPT file. |
Definition of a Polygon |

|
INSTRUCTIONAL RESOURCE: Math Examples 64 | MATH EXAMPLES--The Language of Math--Numerical Expressions--Addition
This set of tutorials provides 40 examples of converting verbal expressions into numerical expressions that involve addition. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 65 | MATH EXAMPLES--The Language of Math--Numerical Expressions--Division
This set of tutorials provides 40 examples of converting verbal expressions into numerical expressions that involve division. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 66 | MATH EXAMPLES--The Language of Math--Numerical Expressions--Grouping Symbols
This set of tutorials provides 32 examples of converting verbal expressions into numerical expressions that involve grouping symbols. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 67 | MATH EXAMPLES--The Language of Math--Numerical Expressions--Multiplication
This set of tutorials provides 40 examples of converting verbal expressions into numerical expressions that involve multiplication. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 68 | MATH EXAMPLES--The Language of Math--Numerical Expressions--Subtraction
This set of tutorials provides 40 examples of converting verbal expressions into numerical expressions that involve subtraction. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 69 | MATH EXAMPLES--The Language of Math--Variable Expressions--Multiplication and Addition
This set of tutorials provides 32 examples of converting verbal expressions into variable expressions that involve multiplication and addition. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
INSTRUCTIONAL RESOURCE: Math Examples 70 | MATH EXAMPLES--The Language of Math--Variable Expressions--Multiplication and Subtraction
This set of tutorials provides 32 examples of converting verbal expressions into variable expressions that involve multiplication and subtraction. Note: The download is a PPT file. NOTE: The download is a PPT file. |
Numerical and Algebraic Expressions |

|
Interactive Crossword Puzzle--Triangles | Interactive Crossword Puzzle--Triangles
This interactive crossword puzzle tests knowledge of key terms on the topic of triangles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Triangle |

|
Interactive Math Game--DragNDrop--The Language of Math--Numerical Expressions--Addition | Interactive Math Game--DragNDrop Math--The Language of Math--Numerical Expressions--Addition
In this drag-and-drop game, a verbal expression to a numerical expression with addition. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |

|
Interactive Math Game--DragNDrop--The Language of Math--Numerical Expressions--Division | Interactive Math Game--DragNDrop Math--The Language of Math--Numerical Expressions--Division
In this drag-and-drop game, match a verbal description of an addition expression with its numerical counterpart. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |

|
Interactive Math Game--DragNDrop--The Language of Math--Numerical Expressions--Grouping Symbols | Interactive Math Game--DragNDrop Math--The Language of Math--Numerical Expressions--Grouping Symbols
In this drag-and-drop game, a verbal expression to a numerical expression with grouping symbols. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |

|
Interactive Math Game--DragNDrop--The Language of Math--Numerical Expressions--Multiplication | Interactive Math Game--DragNDrop Math--The Language of Math--Numerical Expressions--Multiplication
In this drag-and-drop game, match a verbal expression to a numerical expression with multiplication. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |

|
Interactive Math Game--DragNDrop--The Language of Math--Numerical Expressions--Subtraction | Interactive Math Game--DragNDrop Math--The Language of Math--Numerical Expressions--Subtraction
In this drag-and-drop game, match a verbal description of a subtraction expression with its numerical counterpart. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |

|
Interactive Math Game--DragNDrop--The Language of Math--Variable Expressions--Multiplication and Addition | Interactive Math Game--DragNDrop Math--The Language of Math--Variable Expressions--Multiplication and Addition
In this drag-and-drop game, a verbal expression to a variable expression with multiplication and addition. This game generates thousands of different equation combinations, offering an ideal opportunity for skill review in a game format. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Numerical Expressions and Variable Expressions |