
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 2: Chance Experiments
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Statistics and Probability Concepts--Dependent Event | Dependent EventTopicStatistics and Probability DefinitionA dependent event is an event whose outcome is influenced by the outcome of a preceding event. |
Probability |

|
Definition--Statistics and Probability Concepts--Dependent Event | Dependent EventTopicStatistics and Probability DefinitionA dependent event is an event whose outcome is influenced by the outcome of a preceding event. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |

|
Definition--Statistics and Probability Concepts--Independent Event | Independent EventTopicStatistics and Probability DefinitionAn independent event is an event whose outcome is not affected by the outcome of another event. DescriptionIndependent events are a key concept in probability, where the occurrence of one event does not influence another. This principle is applied in various fields, such as quality control, where the failure of one product does not affect others. Understanding independent events is essential for students to accurately calculate probabilities and analyze situations where events occur without influencing each other. |
Probability |
|
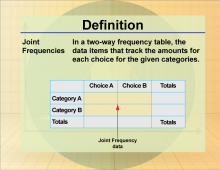
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Joint Frequencies | Joint FrequenciesTopicStatistics and Probability DefinitionJoint frequencies refer to the counts of occurrences for combinations of two categorical variables. DescriptionIn statistics, joint frequencies are used to analyze the relationship between two categorical variables, often displayed in a contingency table. This analysis is vital in fields such as market research, where understanding the joint distribution of consumer preferences can inform product development. For students, learning about joint frequencies is important for interpreting data from surveys and experiments, allowing them to explore relationships between variables effectively. |
Data Analysis |
|
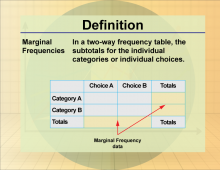
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Marginal Frequencies | Marginal FrequenciesTopicStatistics and Probability DefinitionMarginal frequencies are the totals of rows or columns in a contingency table, representing the sum of joint frequencies for each category. DescriptionMarginal frequencies provide insight into the overall distribution of each variable in a dataset. They are crucial in fields like epidemiology, where understanding the marginal distribution of diseases can inform public health strategies. For students, comprehending marginal frequencies is essential for summarizing data and drawing conclusions about the prevalence of certain characteristics within a population. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Multiplication Rule of Probability | Multiplication Rule of ProbabilityTopicStatistics and Probability DefinitionThe multiplication rule of probability is used to find the probability of two independent events both occurring. DescriptionThe multiplication rule is essential in probability for calculating the likelihood of multiple independent events occurring together. This rule is applied in fields such as genetics, where the probability of inheriting multiple traits is determined. For students, understanding the multiplication rule is crucial for solving problems involving the probability of compound events and for developing a deeper understanding of probability theory. |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 1 | Permutation 1TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is |
Data Analysis |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |

|
Definition--Statistics and Probability Concepts--Permutation 2 | Permutation 2TopicStatistics and Probability DefinitionA permutation is an arrangement of items in a specific order. DescriptionPermutations are used in probability and combinatorics to determine the number of ways to arrange a set of items, which is crucial in fields like cryptography, where secure codes are generated. The formula for permutations is
|
Probability |
|
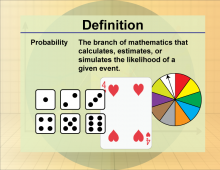
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability | ProbabilityTopicStatistics and Probability DefinitionProbability quantifies the likelihood of an event occurring. DescriptionProbability is a key concept in statistics that assesses the chance that a specific event will occur out of all possible outcomes. This concept is widely used in various fields such as gambling, insurance, and any scenario involving uncertainty. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |

|
Definition--Statistics and Probability Concepts--Probability Model | Probability ModelTopicStatistics and Probability DefinitionA probability model is a mathematical representation of a random phenomenon. DescriptionProbability models are essential in understanding how to quantify uncertainty in various scenarios. They can be as simple as a coin toss or as complex as predicting stock market trends. These models usually incorporate the outcomes of an event and their associated probabilities. |
Probability |