
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 3: More Costs of Running a Restaurant
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Closed Captioned Video: Ratios: Unit Rates | Closed Captioned Video: Ratios: Unit RatesTopicRatios DescriptionThe video focuses on unit rates, where the denominator equals one. It includes practical examples like finding the cost per pound of bananas or determining hourly wages. Applications extend to conversions and scaling calculations for various real-world tasks. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax | Calculating TaxTopicRatios, Proportions, and Percents DefinitionCalculating tax involves determining the percentage amount to be added to the base price of a product or service. DescriptionCalculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tips | Calculating TipsTopicRatios, Proportions, and Percents DefinitionCalculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill. DescriptionCalculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 80 × 0.15 = 12 |
Applications of Ratios, Proportions, and Percents |
|
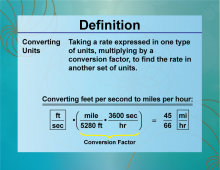
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |