
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 3: More Costs of Running a Restaurant
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |
|
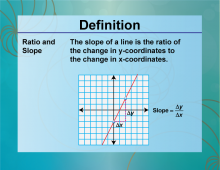
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents | Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |
|
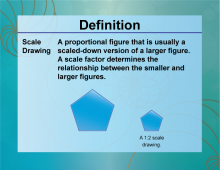
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |