
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 5: How Crowded Is this Neighborhood?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
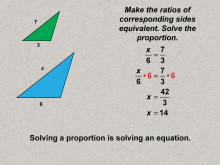
Math Clip Art--Ratios, Proportions, Percents--Proportions 09 | Math Clip Art--Ratios, Proportions, Percents--Proportions 09TopicRatios, Proportions, and Percents DescriptionThis image solves the posed proportion problem by finding the value of x using equivalent ratios (x/6 = 7/3). It breaks down the process of solving proportions, reinforcing mathematical reasoning. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 1 | Math Example--Area and Perimeter--Quadrilaterals: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units. Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 1 | Math Example--Area and Perimeter--Quadrilaterals: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units. Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 1 | Math Example--Area and Perimeter--Quadrilaterals: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a square. The square ABCD has sides measuring 3 units each. To find the area, we use the formula A = s², where s is the length of a side. In this case, A = 3² = 9 square units. Understanding area and perimeter of quadrilaterals is a fundamental concept in geometry. This collection of examples helps students grasp these concepts by providing visual representations and step-by-step calculations for various quadrilaterals. By exploring different shapes and sizes, students develop a deeper understanding of how dimensions relate to area and perimeter. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 10 | Math Example--Area and Perimeter--Quadrilaterals: Example 10TopicGeometry DescriptionThis example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 10 | Math Example--Area and Perimeter--Quadrilaterals: Example 10TopicGeometry DescriptionThis example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 10 | Math Example--Area and Perimeter--Quadrilaterals: Example 10TopicGeometry DescriptionThis example demonstrates the calculation of a rhombus's area using algebraic expressions. The rhombus has a base of x + 6 units and a height of x - 2 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 6)(x - 2) = x² + 4x - 12 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 11 | Math Example--Area and Perimeter--Quadrilaterals: Example 11TopicGeometry DescriptionThis example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 11 | Math Example--Area and Perimeter--Quadrilaterals: Example 11TopicGeometry DescriptionThis example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 11 | Math Example--Area and Perimeter--Quadrilaterals: Example 11TopicGeometry DescriptionThis example illustrates how to calculate the area of a kite using its diagonals. The kite has diagonals measuring 25 units and 19 units. To find the area of a kite, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = (25 × 19) ÷ 2 = 475 ÷ 2 = 237.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 12 | Math Example--Area and Perimeter--Quadrilaterals: Example 12TopicGeometry DescriptionThis example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 12 | Math Example--Area and Perimeter--Quadrilaterals: Example 12TopicGeometry DescriptionThis example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 12 | Math Example--Area and Perimeter--Quadrilaterals: Example 12TopicGeometry DescriptionThis example demonstrates the calculation of a kite's area using algebraic expressions for its diagonals. The kite has diagonals measuring x + 11 units and x - 5 units. To find the area, we use the formula A = (d₁ × d₂) ÷ 2, where d₁ and d₂ are the lengths of the diagonals. In this case, A = [(x + 11)(x - 5)] ÷ 2 = (x² + 6x - 55) ÷ 2 = ½x² + 3x - 27.5 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 13 | Math Example--Area and Perimeter--Quadrilaterals: Example 13TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 13 | Math Example--Area and Perimeter--Quadrilaterals: Example 13TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 13 | Math Example--Area and Perimeter--Quadrilaterals: Example 13TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a square. The square ABCD has sides measuring 6 units each. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 6 = 24 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 14 | Math Example--Area and Perimeter--Quadrilaterals: Example 14TopicGeometry DescriptionThis example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units. Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 14 | Math Example--Area and Perimeter--Quadrilaterals: Example 14TopicGeometry DescriptionThis example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units. Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 14 | Math Example--Area and Perimeter--Quadrilaterals: Example 14TopicGeometry DescriptionThis example illustrates the calculation of a square's perimeter using an algebraic expression. The square ABCD has sides measuring x + 15 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 15) = 4x + 60 units. Incorporating algebra into geometry problems helps students connect different mathematical concepts and develop more advanced problem-solving skills. This collection of examples bridges the gap between basic geometry and algebraic thinking, preparing students for more complex mathematical challenges they will encounter in higher-level courses. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 15 | Math Example--Area and Perimeter--Quadrilaterals: Example 15TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 15 | Math Example--Area and Perimeter--Quadrilaterals: Example 15TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 15 | Math Example--Area and Perimeter--Quadrilaterals: Example 15TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rectangle. The rectangle ABCD has a length of 18 units and a width of 12 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2(18 + 12) = 2(30) = 60 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |
|
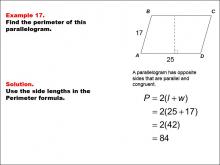
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |
|
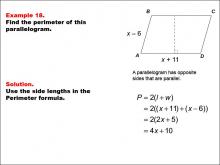
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |