
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 5: How Crowded Is this Neighborhood?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Area and Perimeter--Quadrilaterals: Example 16 | Math Example--Area and Perimeter--Quadrilaterals: Example 16TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's perimeter using algebraic expressions. The rectangle ABCD has a length of x + 25 units and a width of x - 7 units. To find the perimeter, we use the formula P = 2(l + w), where l is the length and w is the width. In this case, P = 2[(x + 25) + (x - 7)] = 2(2x + 18) = 4x + 36 units. |
Area and Perimeter of Quadrilaterals |
|
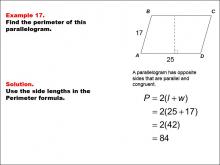
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 17 | Math Example--Area and Perimeter--Quadrilaterals: Example 17TopicGeometry DescriptionThis example illustrates how to calculate the perimeter of a parallelogram. The parallelogram ABCD has side lengths of 17 units and 25 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2(17 + 25) = 2(42) = 84 units. |
Area and Perimeter of Quadrilaterals |
|
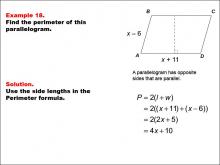
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 18 | Math Example--Area and Perimeter--Quadrilaterals: Example 18TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's perimeter using algebraic expressions. The parallelogram ABCD has side lengths of x + 11 units and x - 6 units. To find the perimeter, we use the formula P = 2(l + w), where l and w are the lengths of the two different sides. In this case, P = 2[(x + 11) + (x - 6)] = 2(2x + 5) = 4x + 10 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 19 | Math Example--Area and Perimeter--Quadrilaterals: Example 19TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a trapezoid. The trapezoid ABCD has sides measuring 22, 17, 14, and 16 units. To find the perimeter, we simply add all four side lengths. In this case, P = 22 + 17 + 14 + 16 = 69 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 2 | Math Example--Area and Perimeter--Quadrilaterals: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a square's area using algebraic expressions. The square ABCD has sides measuring x + 5 units. To find the area, we use the formula A = s², where s is the side length. Here, we have A = (x + 5)² = x² + 10x + 25 square units. Incorporating algebra into geometry problems helps students connect different mathematical concepts. This collection of examples bridges the gap between basic geometry and more advanced mathematical thinking. By working with variables and expressions, students develop skills in both geometric reasoning and algebraic manipulation. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 20 | Math Example--Area and Perimeter--Quadrilaterals: Example 20TopicGeometry DescriptionThis example illustrates the calculation of a trapezoid's perimeter using algebraic expressions. The trapezoid ABCD has sides measuring x + 8, x + 6, x - 1, and x + 5 units. To find the perimeter, we add all four side lengths. In this case, P = (x + 8) + (x + 6) + (x - 1) + (x + 5) = 4x + 18 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 21 | Math Example--Area and Perimeter--Quadrilaterals: Example 21TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a rhombus. The rhombus ABCD has all sides measuring 35 units. To find the perimeter, we use the formula P = 4s, where s is the length of a side. In this case, P = 4 × 35 = 140 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 22 | Math Example--Area and Perimeter--Quadrilaterals: Example 22TopicGeometry DescriptionThis example illustrates the calculation of a rhombus's perimeter using an algebraic expression. The rhombus ABCD has all sides measuring x + 14 units. To find the perimeter, we use the formula P = 4s, where s is the side length. In this case, P = 4(x + 14) = 4x + 56 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 23 | Math Example--Area and Perimeter--Quadrilaterals: Example 23TopicGeometry DescriptionThis example demonstrates how to calculate the perimeter of a kite. The kite ABCD has two pairs of equal sides: AB and AD measure 22 units each, while BC and CD measure 11 units each. To find the perimeter, we add all four side lengths. In this case, P = 22 + 22 + 11 + 11 = 66 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 24 | Math Example--Area and Perimeter--Quadrilaterals: Example 24TopicGeometry DescriptionThis example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 24 | Math Example--Area and Perimeter--Quadrilaterals: Example 24TopicGeometry DescriptionThis example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 24 | Math Example--Area and Perimeter--Quadrilaterals: Example 24TopicGeometry DescriptionThis example illustrates the calculation of a kite's perimeter using algebraic expressions. The kite ABCD has two pairs of equal sides: AB and AD measure x + 11 units each, while BC and CD measure x - 5 units each. To find the perimeter, we add all four side lengths. In this case, P = (x + 11) + (x + 11) + (x - 5) + (x - 5) = 4x + 12 units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 3 | Math Example--Area and Perimeter--Quadrilaterals: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 3 | Math Example--Area and Perimeter--Quadrilaterals: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 3 | Math Example--Area and Perimeter--Quadrilaterals: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of a rectangle. The rectangle ABCD has a length of 12 units and a width of 8 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = 12 × 8 = 96 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 4 | Math Example--Area and Perimeter--Quadrilaterals: Example 4TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 4 | Math Example--Area and Perimeter--Quadrilaterals: Example 4TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 4 | Math Example--Area and Perimeter--Quadrilaterals: Example 4TopicGeometry DescriptionThis example demonstrates the calculation of a rectangle's area using algebraic expressions. The rectangle ABCD has a length of x + 10 units and a width of x - 3 units. To find the area, we use the formula A = l × w, where l is the length and w is the width. In this case, A = (x + 10)(x - 3) = x² + 7x - 30 square units. |
Area and Perimeter of Quadrilaterals |
|
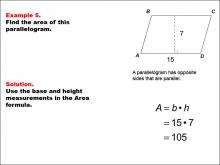
Math Example--Area and Perimeter--Quadrilaterals: Example 5 | Math Example--Area and Perimeter--Quadrilaterals: Example 5TopicGeometry DescriptionThis example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 5 | Math Example--Area and Perimeter--Quadrilaterals: Example 5TopicGeometry DescriptionThis example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 5 | Math Example--Area and Perimeter--Quadrilaterals: Example 5TopicGeometry DescriptionThis example illustrates how to calculate the area of a parallelogram. The parallelogram ABCD has a base of 15 units and a height of 7 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 15 × 7 = 105 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 6 | Math Example--Area and Perimeter--Quadrilaterals: Example 6TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 6 | Math Example--Area and Perimeter--Quadrilaterals: Example 6TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 6 | Math Example--Area and Perimeter--Quadrilaterals: Example 6TopicGeometry DescriptionThis example demonstrates the calculation of a parallelogram's area using algebraic expressions. The parallelogram ABCD has a base of x + 9 units and a height of x - 4 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 9)(x - 4) = x² + 5x - 36 square units. |
Area and Perimeter of Quadrilaterals |
|
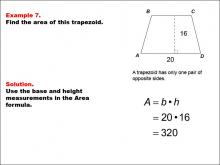
Math Example--Area and Perimeter--Quadrilaterals: Example 7 | Math Example--Area and Perimeter--Quadrilaterals: Example 7TopicGeometry DescriptionThis example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 7 | Math Example--Area and Perimeter--Quadrilaterals: Example 7TopicGeometry DescriptionThis example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 7 | Math Example--Area and Perimeter--Quadrilaterals: Example 7TopicGeometry DescriptionThis example illustrates how to calculate the area of a trapezoid. The trapezoid ABCD has a base of 20 units and a height of 16 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = 20 × 16 = 320 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 8 | Math Example--Area and Perimeter--Quadrilaterals: Example 8TopicGeometry DescriptionThis example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 8 | Math Example--Area and Perimeter--Quadrilaterals: Example 8TopicGeometry DescriptionThis example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 8 | Math Example--Area and Perimeter--Quadrilaterals: Example 8TopicGeometry DescriptionThis example demonstrates the calculation of a trapezoid's area using algebraic expressions. The trapezoid ABCD has a base of x + 12 units and a height of x - 5 units. To find the area, we use the formula A = b × h, where b is the base and h is the height. In this case, A = (x + 12)(x - 5) = x² + 7x - 60 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 9 | Math Example--Area and Perimeter--Quadrilaterals: Example 9TopicGeometry DescriptionThis example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 9 | Math Example--Area and Perimeter--Quadrilaterals: Example 9TopicGeometry DescriptionThis example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units. |
Area and Perimeter of Quadrilaterals |

|
Math Example--Area and Perimeter--Quadrilaterals: Example 9 | Math Example--Area and Perimeter--Quadrilaterals: Example 9TopicGeometry DescriptionThis example illustrates how to calculate the area of a rhombus. The rhombus ABCD has a side length of 25 units and a height (perpendicular distance between parallel sides) of 19 units. To find the area, we use the formula A = b × h, where b is the base (which is the same as the side length in a rhombus) and h is the height. In this case, A = 25 × 19 = 475 square units. |
Area and Perimeter of Quadrilaterals |
|
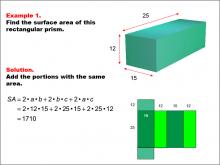
Math Example--Area and Perimeter--Surface Area: Example 1 | Math Example--Area and Perimeter--Surface Area: Example 1TopicSurface Area DescriptionThis example demonstrates the calculation of surface area for a rectangular prism. The prism has dimensions of 25, 15, and 12 units. The surface area is determined by summing the areas of all faces, which is represented by the formula SA = 2ab + 2bc + 2ac. For this specific prism, the calculation yields a surface area of 1710 square units. |
Surface Area |