Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 5: How Crowded Is this Neighborhood?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
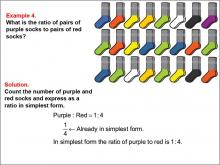
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
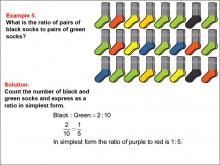
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
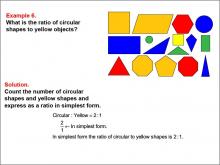
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
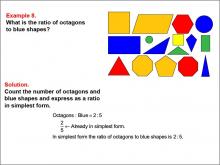
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
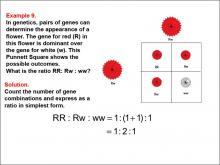
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
|
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17
This is part of a collection of math examples that focus on ratios, proportions, and percents. |
Proportions |
