
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 6: Fermi Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |
|
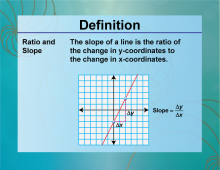
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios in Simplest Form | Ratios in Simplest FormTopicRatios, Proportions, and Percents DefinitionRatios in simplest form are ratios that have been reduced to their smallest whole number terms. DescriptionReducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1. For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities. |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals | Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions | Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |