Illustrative Math Alignment: Grade 7 Unit 9

Putting it All Together

Lesson 6: Fermi Problems

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
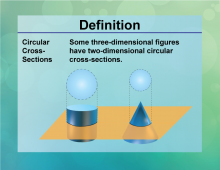
Definition--Circle Concepts--Circular Cross-Sections	Circular Cross-Sections Topic Circles Definition Circular cross-sections are the intersections of a plane with a solid that result in a circle.	Definition of a Circle
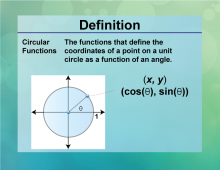
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Functions	Circular Functions Topic Circles Definition Circular functions are trigonometric functions that relate angles to ratios of sides in a right triangle.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
Definition--Circle Concepts--Circular Models	Circular Models Topic Circles Definition Circular models are representations of circular phenomena using mathematical equations and diagrams.	Definition of a Circle
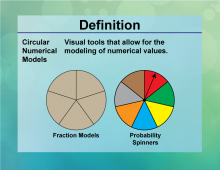
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
Definition--Circle Concepts--Circular Numerical Models	Circular Numerical Models Topic Circles Definition Circular numerical models use numerical methods to analyze and simulate circular phenomena.	Definition of a Circle
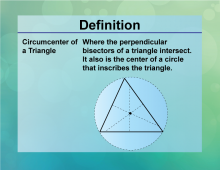
Definition--Circle Concepts--Circumcenter of Triangle	Circumcenter of Triangle Topic Circles Definition The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices.	Definition of a Circle
Definition--Circle Concepts--Circumcenter of Triangle	Circumcenter of Triangle Topic Circles Definition The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices.	Definition of a Circle
Definition--Circle Concepts--Circumcenter of Triangle	Circumcenter of Triangle Topic Circles Definition The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices.	Definition of a Circle
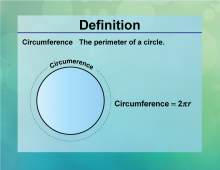
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
Definition--Circle Concepts--Circumference	Circumference Topic Circles Definition The circumference of a circle is the distance around the circle, calculated as C = 2πr. Description The circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr	Definition of a Circle
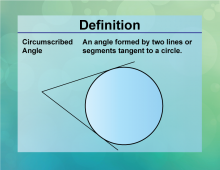
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Circumscribed Angle	Circumscribed Angle Topic Circles Definition A circumscribed angle is an angle formed outside a circle by two intersecting tangents.	Definition of a Circle
Definition--Circle Concepts--Concentric Circles	Concentric Circles Topic Circles Definition Concentric circles are circles that share the same center but have different radii.	Definition of a Circle
Definition--Circle Concepts--Concentric Circles	Concentric Circles Topic Circles Definition Concentric circles are circles that share the same center but have different radii.	Definition of a Circle
Definition--Circle Concepts--Concentric Circles	Concentric Circles Topic Circles Definition Concentric circles are circles that share the same center but have different radii.	Definition of a Circle
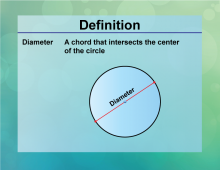
Definition--Circle Concepts--Diameter	Diameter Topic Circles Definition The diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. Description The diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr	Definition of a Circle
Definition--Circle Concepts--Diameter	Diameter Topic Circles Definition The diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. Description The diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr	Definition of a Circle
Definition--Circle Concepts--Diameter	Diameter Topic Circles Definition The diameter of a circle is a line segment that passes through the center and has its endpoints on the circle, calculated as D = 2πr. Description The diameter is a fundamental concept in geometry, representing the longest distance across a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula D = 2πr	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
Definition--Circle Concepts--Equation of a Circles	Equation of a Circle Topic Circles Definition The equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius.	Definition of a Circle
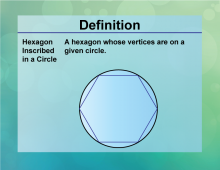
Definition--Circle Concepts--Hexagon Inscribed in a Circle	Hexagon Inscribed in a Circle Topic Circles Definition A hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle.	Definition of a Circle
Definition--Circle Concepts--Hexagon Inscribed in a Circle	Hexagon Inscribed in a Circle Topic Circles Definition A hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle.	Definition of a Circle
Definition--Circle Concepts--Hexagon Inscribed in a Circle	Hexagon Inscribed in a Circle Topic Circles Definition A hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle.	Definition of a Circle
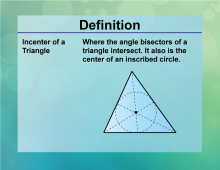
Definition--Circle Concepts--Incenter of a Triangle	Incenter of a Triangle Topic Circles Definition The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.	Definition of a Circle
Definition--Circle Concepts--Incenter of a Triangle	Incenter of a Triangle Topic Circles Definition The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.	Definition of a Circle
Definition--Circle Concepts--Incenter of a Triangle	Incenter of a Triangle Topic Circles Definition The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.	Definition of a Circle
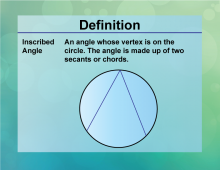
Definition--Circle Concepts--Inscribed Angle	Inscribed Angle Topic Circles Definition An inscribed angle is an angle formed by two chords in a circle that share an endpoint.	Definition of a Circle
Definition--Circle Concepts--Inscribed Angle	Inscribed Angle Topic Circles Definition An inscribed angle is an angle formed by two chords in a circle that share an endpoint.	Definition of a Circle
Definition--Circle Concepts--Inscribed Angle	Inscribed Angle Topic Circles Definition An inscribed angle is an angle formed by two chords in a circle that share an endpoint.	Definition of a Circle
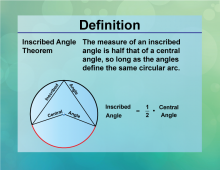
Definition--Circle Concepts--Inscribed Angle Theorem	Inscribed Angle Theorem Topic Circles Definition The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc.	Definition of a Circle
Definition--Circle Concepts--Inscribed Angle Theorem	Inscribed Angle Theorem Topic Circles Definition The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc.	Definition of a Circle
Definition--Circle Concepts--Inscribed Angle Theorem	Inscribed Angle Theorem Topic Circles Definition The inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc.	Definition of a Circle
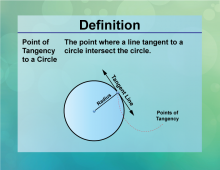
Definition--Circle Concepts--Point of Tangency to a Circle	Point of Tangency to a Circle Topic Circles Definition The point of tangency is the point where a tangent line touches the circle.	Definition of a Circle
Definition--Circle Concepts--Point of Tangency to a Circle	Point of Tangency to a Circle Topic Circles Definition The point of tangency is the point where a tangent line touches the circle.	Definition of a Circle
Definition--Circle Concepts--Point of Tangency to a Circle	Point of Tangency to a Circle Topic Circles Definition The point of tangency is the point where a tangent line touches the circle.	Definition of a Circle
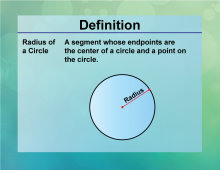
Definition--Circle Concepts--Radius of a Circle	Radius of a Circle Topic Circles Definition The radius of a circle is a line segment from the center to any point on the circle.	Definition of a Circle
Definition--Circle Concepts--Radius of a Circle	Radius of a Circle Topic Circles Definition The radius of a circle is a line segment from the center to any point on the circle.	Definition of a Circle
Definition--Circle Concepts--Radius of a Circle	Radius of a Circle Topic Circles Definition The radius of a circle is a line segment from the center to any point on the circle.	Definition of a Circle
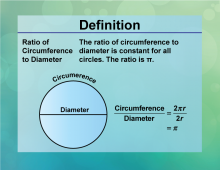
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle
Definition--Circle Concepts--Ratio of Circumference to Diameter	Ratio of Circumference to Diameter Topic Circles Definition The ratio of the circumference to the diameter of a circle is the constant π.	Definition of a Circle