
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 12: Solutions to Linear Equations
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Paper-and-Pencil Quiz: Equations with Percents (Easy) | Paper-and-Pencil Quiz: Equations with Percents (Easy)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Paper-and-Pencil Quiz: Equations with Percents (Hard) | Paper-and-Pencil Quiz: Equations with Percents (Hard)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Paper-and-Pencil Quiz: Equations with Percents (Medium) | Paper-and-Pencil Quiz: Equations with Percents (Medium)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Slope Formula (Easy) | Paper-and-Pencil Quiz: Slope Formula (Easy)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Paper-and-Pencil Quiz: Slope Formula (Hard) | Paper-and-Pencil Quiz: Slope Formula (Hard)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Paper-and-Pencil Quiz: Slope Formula (Medium) | Paper-and-Pencil Quiz: Slope Formula (Medium)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Promethean Flipchart: Algebra Applications: Honey Production | Honey bees not only produce a tasty treat, they also help pollinate flowering plants that provide much of the food throughout the world. So, when in 2006 bee colonies started dying out, scientists recognized a serious problem. Analyzing statistics from honey bee production allows for a mathematical analysis of the so-called Colony Collapse Disorder. Note: The download for this resources is the Promethean Flipchart. To access the full video [Algebra Applications: Variables and Equations, Segment 2: Honey Production]: https://www.media4math.com/library/algebra-applications-variables-and-equations-segment-2-honey-production |
Applications of Equations and Inequalities |

|
Promethean Flipchart: Algebra Jeopardy | In this Promethean Flipchart, review key concepts from linear functions using a Jeopardy-style game. Note: The download for this resources is the Promethean Flipchart. | Applications of Equations and Inequalities |

|
Promethean Flipchart: Algebra Nspirations: Variables and Equations | Ever since the mathematics of the Babylonians, equations have played a central role in the development of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video traces the history and evolution of equations. It explores the two principal equations encountered in an introductory algebra course – linear and quadratic – in an engaging way. The foundations of algebra are explored and fundamental questions about the nature of algebra are answered. In addition, problems involving linear and quadratic equations are solved using the TI-Nspire graphing calculator. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. |
Applications of Equations and Inequalities |

|
Quizlet Flash Cards: Slope Formula, Set 01 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 02 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 03 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 04 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 05 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 06 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 07 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 08 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 09 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 10 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 01 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 02 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 03 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 04 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 05 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 06 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 07 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 08 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 09 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |

|
Quizlet Flash Cards: Subtracting Variable Expressions, Set 10 | Subtract variable expressions in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3eUis7V |
Variable Expressions |
|
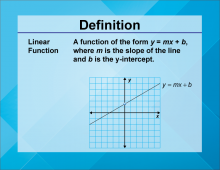
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |
|
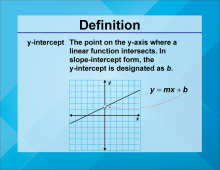
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |
|
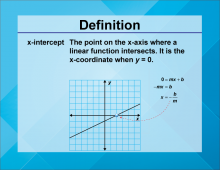
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |
|
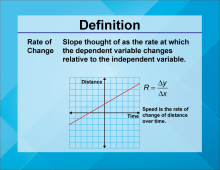
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing. |
Slope-Intercept Form |
|
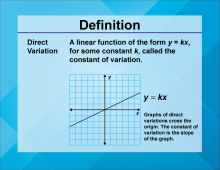
Video Definition 17--Linear Function Concepts--Direct Variation | Video Definition 17--Linear Function Concepts--Direct Variation
TopicLinear Functions DescriptionThe term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics. |
Slope-Intercept Form |
|
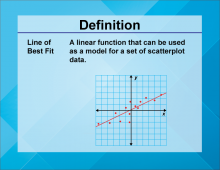
Video Definition 18--Linear Function Concepts--Line of Best Fit | Video Definition 18--Linear Function Concepts--Line of Best Fit
TopicLinear Functions DescriptionThe term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends. |
Graphs of Linear Functions |
|
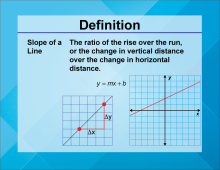
Video Definition 19--Linear Function Concepts--Slope | Video Definition 19--Linear Function Concepts--Slope
TopicLinear Functions DescriptionThe term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction. |
Slope |
|
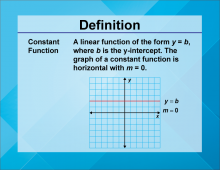
Video Definition 2--Linear Function Concepts--Constant Function | Video Definition 2--Linear Function Concepts--Constant Function
TopicLinear Functions DescriptionThe term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines. |
Slope-Intercept Form |

|
Video Definition 20--Linear Function Concepts--System of Linear Equations | Video Definition 20--Linear Function Concepts--System of Linear Equations
TopicLinear Functions DescriptionThe term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation | Video Definition 21--Linear Function Concepts--Solution to a Linear Equation
TopicLinear Functions DescriptionThe term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables. |
Solving Systems of Equations |

|
Video Definition 22--Linear Function Concepts--Proportional Relationship | Video Definition 22--Linear Function Concepts--Proportional Relationship
TopicLinear Functions DescriptionThe term is "Proportional Relationship," defined as a type of linear relationship where two variables maintain a constant ratio. Represented as y = kx, where k is the constant ratio. This term establishes the foundation for understanding direct variation and proportionality in linear relationships. |
Proportions |
|
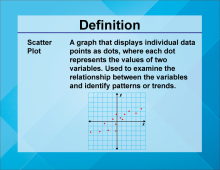
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |
|
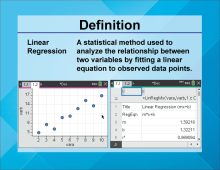
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |