Illustrative Math Alignment: Grade 8 Unit 3

Linear Relationships

Lesson 12: Solutions to Linear Equations

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Definition--Direct Variation	Direct Variation Topic Linear Functions Definition Direct variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. Description Direct variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering.	Applications of Linear Functions
Definition--Order of Operations	Definition--Order of Operations Watch the following video on Order of Operations. (The transcript is included.) Video Transcript A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division. Because addition is commutative, adding from left to right, or right to left, gives you the same result. The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations. Subtraction isn't commutative.	Numerical Expressions and Variable Expressions
Definition--Slope Concepts--Delta x	Delta x Topic Slope Definition Delta x is the change in the x-coordinate in a linear relationship. Description The term Delta x is fundamental to understanding slope as it represents the horizontal change in a line’s position. In real-world applications, Delta x can represent the distance traveled over time in physics and engineering contexts.	Slope
Definition--Slope Concepts--Delta y	Delta y Topic Slope Definition Delta y is the change in the y-coordinate in a linear relationship. Description The term Delta y signifies the vertical change, essential for calculating slope used in graphing and data interpretation. In practical scenarios, Delta y can illustrate changes in temperature over time or the rise in elevation in geography.	Slope
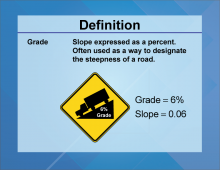
Definition--Slope Concepts--Grade	Grade Topic Slope Definition Grade is a ratio indicating the steepness of a slope. Description The term Grade commonly refers to the angle of elevation or slope expressed as a percentage. In engineering, grades are crucial for designing roads and railways, ensuring safety and efficiency.	Slope
Definition--Slope Concepts--Gradient	Gradient Topic Slope Definition Gradient represents the rate of change of a quantity. Description The Gradient measures how steep a line is, calculated by the ratio of the rise to run. This concept is significant in fields like physics and economics where gradients can represent relationships between variables.	Slope
Definition--Slope Concepts--Negative Slope	Negative Slope Topic Slope Definition Negative Slope indicates a decrease in value as x increases. Description The Negative Slope signifies that as one variable increases, the other decreases, often used in economics to depict inverse relationships. This term finds relevance in real-world scenarios like demand curves which slope downwards.	Slope
Definition--Slope Concepts--Pitch	Pitch Topic Slope Definition Pitch refers to the steepness of a slope in a real-world context. Description Pitch is commonly applied in construction and design fields to denote the angle of roofs and ramps. This is essential in architecture, especially when dealing with drainage and material use.	Slope
Definition--Slope Concepts--Point-Slope Form	Point-Slope Form Topic Slope Definition Point-Slope Form is a way to express linear equations given the slope and a point on the line. Description The Point-Slope Form is crucial in algebra for identifying linear relationships given the slope and a point on the line. Understanding this concept aids in graphing lines efficiently and is foundational in higher mathematics. For a complete collection of terms related to Slope click on this link: Slope Collection.	Point-Slope Form
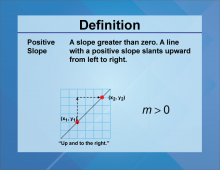
Definition--Slope Concepts--Positive Slope	Positive Slope Topic Slope Definition Positive Slope indicates an increase in value as x increases. Description The Positive Slope indicates that as x grows, y also rises, signifying direct relationships in data analysis. This principle enables predictions in various analytics and trends. For a complete collection of terms related to Slope click on this link: Slope Collection.	Slope
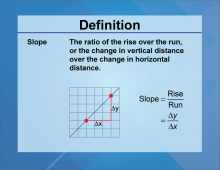
Definition--Slope Concepts--Slope	Slope Topic Slope Definition Slope measures the steepness of a line. Description Slope is a fundamental concept in mathematics, expressing the ratio of vertical rise to horizontal run. This is vital for understanding linear functions, essential in fields such as physics, economics, and data science. For a complete collection of terms related to Slope click on this link: Slope Collection.	Slope
Definition--Slope Concepts--Slope Formula	Slope Formula Topic Slope Definition The Slope Formula calculates the rate of change. Description The Slope Formula is typically represented as This formula is a cornerstone in algebra, enabling students to analyze linear equations effectively.	Slope
Definition--Slope Concepts--Slope-Intercept Form	Slope-Intercept Form Topic Slope Definition The slope-intercept form is an equation of a straight line represented as y = m x + b, where m is the slope and b is the y-intercept. Description The slope-intercept form is a fundamental concept in algebra, providing a straightforward way to graph linear equations. It is widely used in various fields, from economics to physics, to model linear relationships and predict outcomes based on given data. Understanding this form is crucial for students as it lays the foundation for more complex mathematical concepts and real-world applications.	Slope-Intercept Form
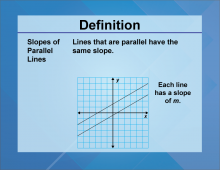
Definition--Slope Concepts--Slopes of Parallel Lines	Slopes of Parallel Lines Topic Slope Definition Parallel lines are lines in the same plane that never meet; they have equal slopes. Description Understanding the slopes of parallel lines is essential in geometry and algebra, as it helps in identifying and proving parallelism in shapes and graphs. This concept is applied in various fields, including architecture and engineering, where maintaining parallelism is crucial for structural integrity and design. In mathematics education, this concept aids in developing logical reasoning and problem-solving skills.	Slope
Definition--Slope Concepts--Slopes of Perpendicular Lines	Slopes of Perpendicular Lines Topic Slope Definition Perpendicular lines intersect at a right angle, and their slopes are negative reciprocals of each other. Description The concept of perpendicular slopes is vital in geometry, as it helps in determining the orthogonality of lines. This principle is used in various applications, such as designing perpendicular intersections in roadways and creating right-angle joints in construction. In education, it enhances students' understanding of geometric properties and their ability to solve related problems.	Slope
Definition--Slope Concepts--Steepness	Steepness Topic Slope Definition Steepness is a measure of how steep a line is, typically calculated as the absolute value of the slope. Description Steepness is a key concept in understanding the inclination of lines and surfaces. It is commonly used in fields like geology and civil engineering to assess the gradient of terrains and structures. In math education, learning about steepness helps students grasp the concept of slope and its practical implications, enhancing their analytical skills and understanding of real-world phenomena.	Slope
Definition--Slope Concepts--The Rise Over the Run	The Rise Over the Run Topic Slope Definition The rise over the run describes the change in y over the change in x in a linear relationship. Description The concept of "rise over run" is foundational in understanding how to calculate the slope of a line. It is used in various disciplines, such as physics and economics, to model relationships and predict trends. In education, mastering this concept is crucial for students as it forms the basis for graphing linear equations and understanding the behavior of lines in a coordinate plane.	Slope
Definition--Slope Concepts--Undefined Slope	Undefined Slope Topic Slope Definition Undefined slope occurs when a vertical line is present, meaning there is no change in x. Description An undefined slope is a critical concept in mathematics, particularly in graphing. It indicates a vertical line where the change in x is zero, making the slope calculation impossible. This concept is important in various fields, such as computer graphics and data analysis, where vertical lines can represent boundaries or limits. Understanding undefined slopes helps students in identifying and interpreting vertical lines in graphs.	Slope
Definition--Slope Concepts--Zero Slope	Zero Slope Topic Slope Definition Zero slope describes a horizontal line where there is no change in y as x changes. Description A zero slope is a key concept in algebra and geometry, representing a horizontal line. It is used in various applications, such as designing flat surfaces and analyzing constant relationships in data. In education, understanding zero slopes helps students in graphing and interpreting horizontal lines, enhancing their ability to analyze linear relationships. For a complete collection of terms related to Slope click on this link: Slope Collection.	Slope
Desmos Activity: Linear Equations in Point-Slope Form	In this graphing calculator activity, have your students explore how to convert linear equations in point-slope to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of coordinates of the point and the slope of the line. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.	Point-Slope Form
Desmos Activity: Linear Equations in Standard Form	Desmos Activity: Linear Equations in Standard Form In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link. The following section includes background information on slope. This background also includes video resources and accompanying transcripts.	Standard Form
Desmos Activity: Slope As Rate of Change	Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost.	Slope and Ratios and Rates
Desmos Activity: Slope As Rise Over Run	Desmos Activity: Slope As Rise Over Run This Desmos activity allows students to explore slope as the ratio of the rise over the run. Click Preview to launch the activity. In the activity students click on the points to create a line segment connecting two points. Use the background grid to determine the rise and the run and calculate the slope.	Slope
Desmos Activity: Slope As Rise Over Run 2	Desmos Activity: Slope As Rise Over Run 2 In this activity, students input different values for the coordinates to create a new line. They can then measure the rise and run to calculate the slope.	Slope
Formulas--Slope Formula	Formulas \| Slope Formula The formula for the Slope Formula. This is part of a collection of math formulas. —PRESS PREVIEW TO SEE THE IMAGE— To see the complete collection of formulas, click on this link. The following section includes background information on slope. This background also includes video resources and accompanying transcripts. What Is Slope? Watch this video to learn about the slope formula. (The transcript is also included.)	Slope
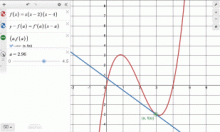
Instructional Resource--Strategy Pack--The Slope of a Line	Instructional Resource \| Strategy Pack \| The Slope of a Line Learn different strategies for finding the slope of a line. The Strategy Packs provide alternate ways of solving the same problem, giving your students different approaches to the same problem. The goal of the Strategy Packs is to encourage your students to think strategically when solving math problems. —PRESS PREVIEW TO LAUNCH THE PRESENTATION— To see the complete collection of Instructional Resources, click on this link. Note: The download is a PPT file.	Slope
Instructional Resource	Instructional Resource \| Using the Point-Slope Form in Calculus In this tutorial, learn how to use the point-slope form to find the equation of the line tangent to a function at a given point. —Click on Preview to see the tutorial—	Calculus Vocabulary
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + -b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Standard Form
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Standard Form
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Standard Form
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Standard Form
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Polynomial Functions and Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Polynomial Functions and Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0 In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Polynomial Functions and Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Polynomial Functions and Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d	INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Solving Two-Step Equations