
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 6: More Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Slope Concepts--Negative Slope | Negative SlopeTopicSlope DefinitionNegative Slope indicates a decrease in value as x increases. DescriptionThe Negative Slope signifies that as one variable increases, the other decreases, often used in economics to depict inverse relationships. This term finds relevance in real-world scenarios like demand curves which slope downwards. |
Slope |

|
Definition--Slope Concepts--Negative Slope | Negative SlopeTopicSlope DefinitionNegative Slope indicates a decrease in value as x increases. DescriptionThe Negative Slope signifies that as one variable increases, the other decreases, often used in economics to depict inverse relationships. This term finds relevance in real-world scenarios like demand curves which slope downwards. |
Slope |

|
Definition--Slope Concepts--Pitch | PitchTopicSlope DefinitionPitch refers to the steepness of a slope in a real-world context. DescriptionPitch is commonly applied in construction and design fields to denote the angle of roofs and ramps. This is essential in architecture, especially when dealing with drainage and material use. |
Slope |

|
Definition--Slope Concepts--Pitch | PitchTopicSlope DefinitionPitch refers to the steepness of a slope in a real-world context. DescriptionPitch is commonly applied in construction and design fields to denote the angle of roofs and ramps. This is essential in architecture, especially when dealing with drainage and material use. |
Slope |

|
Definition--Slope Concepts--Pitch | PitchTopicSlope DefinitionPitch refers to the steepness of a slope in a real-world context. DescriptionPitch is commonly applied in construction and design fields to denote the angle of roofs and ramps. This is essential in architecture, especially when dealing with drainage and material use. |
Slope |

|
Definition--Slope Concepts--Point-Slope Form | Point-Slope FormTopicSlope DefinitionPoint-Slope Form is a way to express linear equations given the slope and a point on the line. DescriptionThe Point-Slope Form is crucial in algebra for identifying linear relationships given the slope and a point on the line. Understanding this concept aids in graphing lines efficiently and is foundational in higher mathematics. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Point-Slope Form |

|
Definition--Slope Concepts--Point-Slope Form | Point-Slope FormTopicSlope DefinitionPoint-Slope Form is a way to express linear equations given the slope and a point on the line. DescriptionThe Point-Slope Form is crucial in algebra for identifying linear relationships given the slope and a point on the line. Understanding this concept aids in graphing lines efficiently and is foundational in higher mathematics. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Point-Slope Form |

|
Definition--Slope Concepts--Point-Slope Form | Point-Slope FormTopicSlope DefinitionPoint-Slope Form is a way to express linear equations given the slope and a point on the line. DescriptionThe Point-Slope Form is crucial in algebra for identifying linear relationships given the slope and a point on the line. Understanding this concept aids in graphing lines efficiently and is foundational in higher mathematics. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Point-Slope Form |
|
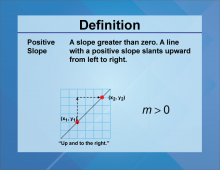
Definition--Slope Concepts--Positive Slope | Positive SlopeTopicSlope DefinitionPositive Slope indicates an increase in value as x increases. DescriptionThe Positive Slope indicates that as x grows, y also rises, signifying direct relationships in data analysis. This principle enables predictions in various analytics and trends. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Positive Slope | Positive SlopeTopicSlope DefinitionPositive Slope indicates an increase in value as x increases. DescriptionThe Positive Slope indicates that as x grows, y also rises, signifying direct relationships in data analysis. This principle enables predictions in various analytics and trends. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Positive Slope | Positive SlopeTopicSlope DefinitionPositive Slope indicates an increase in value as x increases. DescriptionThe Positive Slope indicates that as x grows, y also rises, signifying direct relationships in data analysis. This principle enables predictions in various analytics and trends. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |
|
Definition--Slope Concepts--Slope | SlopeTopicSlope DefinitionSlope measures the steepness of a line. DescriptionSlope is a fundamental concept in mathematics, expressing the ratio of vertical rise to horizontal run. This is vital for understanding linear functions, essential in fields such as physics, economics, and data science. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Slope | SlopeTopicSlope DefinitionSlope measures the steepness of a line. DescriptionSlope is a fundamental concept in mathematics, expressing the ratio of vertical rise to horizontal run. This is vital for understanding linear functions, essential in fields such as physics, economics, and data science. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Slope | SlopeTopicSlope DefinitionSlope measures the steepness of a line. DescriptionSlope is a fundamental concept in mathematics, expressing the ratio of vertical rise to horizontal run. This is vital for understanding linear functions, essential in fields such as physics, economics, and data science. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Slope Formula | Slope FormulaTopicSlope DefinitionThe Slope Formula calculates the rate of change. DescriptionThe Slope Formula is typically represented as This formula is a cornerstone in algebra, enabling students to analyze linear equations effectively. |
Slope |

|
Definition--Slope Concepts--Slope Formula | Slope FormulaTopicSlope DefinitionThe Slope Formula calculates the rate of change. DescriptionThe Slope Formula is typically represented as This formula is a cornerstone in algebra, enabling students to analyze linear equations effectively. |
Slope |

|
Definition--Slope Concepts--Slope Formula | Slope FormulaTopicSlope DefinitionThe Slope Formula calculates the rate of change. DescriptionThe Slope Formula is typically represented as This formula is a cornerstone in algebra, enabling students to analyze linear equations effectively. |
Slope |

|
Definition--Slope Concepts--Slope-Intercept Form | Slope-Intercept FormTopicSlope DefinitionThe slope-intercept form is an equation of a straight line represented as y = m x + b, where m is the slope and b is the y-intercept. DescriptionThe slope-intercept form is a fundamental concept in algebra, providing a straightforward way to graph linear equations. It is widely used in various fields, from economics to physics, to model linear relationships and predict outcomes based on given data. Understanding this form is crucial for students as it lays the foundation for more complex mathematical concepts and real-world applications. |
Slope-Intercept Form |

|
Definition--Slope Concepts--Slope-Intercept Form | Slope-Intercept FormTopicSlope DefinitionThe slope-intercept form is an equation of a straight line represented as y = m x + b, where m is the slope and b is the y-intercept. DescriptionThe slope-intercept form is a fundamental concept in algebra, providing a straightforward way to graph linear equations. It is widely used in various fields, from economics to physics, to model linear relationships and predict outcomes based on given data. Understanding this form is crucial for students as it lays the foundation for more complex mathematical concepts and real-world applications. |
Slope-Intercept Form |

|
Definition--Slope Concepts--Slope-Intercept Form | Slope-Intercept FormTopicSlope DefinitionThe slope-intercept form is an equation of a straight line represented as y = m x + b, where m is the slope and b is the y-intercept. DescriptionThe slope-intercept form is a fundamental concept in algebra, providing a straightforward way to graph linear equations. It is widely used in various fields, from economics to physics, to model linear relationships and predict outcomes based on given data. Understanding this form is crucial for students as it lays the foundation for more complex mathematical concepts and real-world applications. |
Slope-Intercept Form |
|
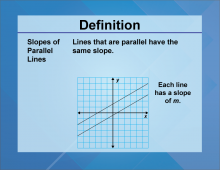
Definition--Slope Concepts--Slopes of Parallel Lines | Slopes of Parallel LinesTopicSlope DefinitionParallel lines are lines in the same plane that never meet; they have equal slopes. DescriptionUnderstanding the slopes of parallel lines is essential in geometry and algebra, as it helps in identifying and proving parallelism in shapes and graphs. This concept is applied in various fields, including architecture and engineering, where maintaining parallelism is crucial for structural integrity and design. In mathematics education, this concept aids in developing logical reasoning and problem-solving skills. |
Slope |

|
Definition--Slope Concepts--Slopes of Parallel Lines | Slopes of Parallel LinesTopicSlope DefinitionParallel lines are lines in the same plane that never meet; they have equal slopes. DescriptionUnderstanding the slopes of parallel lines is essential in geometry and algebra, as it helps in identifying and proving parallelism in shapes and graphs. This concept is applied in various fields, including architecture and engineering, where maintaining parallelism is crucial for structural integrity and design. In mathematics education, this concept aids in developing logical reasoning and problem-solving skills. |
Slope |

|
Definition--Slope Concepts--Slopes of Parallel Lines | Slopes of Parallel LinesTopicSlope DefinitionParallel lines are lines in the same plane that never meet; they have equal slopes. DescriptionUnderstanding the slopes of parallel lines is essential in geometry and algebra, as it helps in identifying and proving parallelism in shapes and graphs. This concept is applied in various fields, including architecture and engineering, where maintaining parallelism is crucial for structural integrity and design. In mathematics education, this concept aids in developing logical reasoning and problem-solving skills. |
Slope |

|
Definition--Slope Concepts--Slopes of Perpendicular Lines | Slopes of Perpendicular LinesTopicSlope DefinitionPerpendicular lines intersect at a right angle, and their slopes are negative reciprocals of each other. DescriptionThe concept of perpendicular slopes is vital in geometry, as it helps in determining the orthogonality of lines. This principle is used in various applications, such as designing perpendicular intersections in roadways and creating right-angle joints in construction. In education, it enhances students' understanding of geometric properties and their ability to solve related problems. |
Slope |

|
Definition--Slope Concepts--Slopes of Perpendicular Lines | Slopes of Perpendicular LinesTopicSlope DefinitionPerpendicular lines intersect at a right angle, and their slopes are negative reciprocals of each other. DescriptionThe concept of perpendicular slopes is vital in geometry, as it helps in determining the orthogonality of lines. This principle is used in various applications, such as designing perpendicular intersections in roadways and creating right-angle joints in construction. In education, it enhances students' understanding of geometric properties and their ability to solve related problems. |
Slope |

|
Definition--Slope Concepts--Slopes of Perpendicular Lines | Slopes of Perpendicular LinesTopicSlope DefinitionPerpendicular lines intersect at a right angle, and their slopes are negative reciprocals of each other. DescriptionThe concept of perpendicular slopes is vital in geometry, as it helps in determining the orthogonality of lines. This principle is used in various applications, such as designing perpendicular intersections in roadways and creating right-angle joints in construction. In education, it enhances students' understanding of geometric properties and their ability to solve related problems. |
Slope |

|
Definition--Slope Concepts--Steepness | SteepnessTopicSlope DefinitionSteepness is a measure of how steep a line is, typically calculated as the absolute value of the slope. DescriptionSteepness is a key concept in understanding the inclination of lines and surfaces. It is commonly used in fields like geology and civil engineering to assess the gradient of terrains and structures. In math education, learning about steepness helps students grasp the concept of slope and its practical implications, enhancing their analytical skills and understanding of real-world phenomena. |
Slope |

|
Definition--Slope Concepts--Steepness | SteepnessTopicSlope DefinitionSteepness is a measure of how steep a line is, typically calculated as the absolute value of the slope. DescriptionSteepness is a key concept in understanding the inclination of lines and surfaces. It is commonly used in fields like geology and civil engineering to assess the gradient of terrains and structures. In math education, learning about steepness helps students grasp the concept of slope and its practical implications, enhancing their analytical skills and understanding of real-world phenomena. |
Slope |

|
Definition--Slope Concepts--Steepness | SteepnessTopicSlope DefinitionSteepness is a measure of how steep a line is, typically calculated as the absolute value of the slope. DescriptionSteepness is a key concept in understanding the inclination of lines and surfaces. It is commonly used in fields like geology and civil engineering to assess the gradient of terrains and structures. In math education, learning about steepness helps students grasp the concept of slope and its practical implications, enhancing their analytical skills and understanding of real-world phenomena. |
Slope |

|
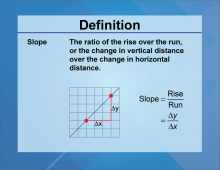
Definition--Slope Concepts--The Rise Over the Run | The Rise Over the RunTopicSlope DefinitionThe rise over the run describes the change in y over the change in x in a linear relationship. DescriptionThe concept of "rise over run" is foundational in understanding how to calculate the slope of a line. It is used in various disciplines, such as physics and economics, to model relationships and predict trends. In education, mastering this concept is crucial for students as it forms the basis for graphing linear equations and understanding the behavior of lines in a coordinate plane. |
Slope |

|
Definition--Slope Concepts--The Rise Over the Run | The Rise Over the RunTopicSlope DefinitionThe rise over the run describes the change in y over the change in x in a linear relationship. DescriptionThe concept of "rise over run" is foundational in understanding how to calculate the slope of a line. It is used in various disciplines, such as physics and economics, to model relationships and predict trends. In education, mastering this concept is crucial for students as it forms the basis for graphing linear equations and understanding the behavior of lines in a coordinate plane. |
Slope |

|
Definition--Slope Concepts--The Rise Over the Run | The Rise Over the RunTopicSlope DefinitionThe rise over the run describes the change in y over the change in x in a linear relationship. DescriptionThe concept of "rise over run" is foundational in understanding how to calculate the slope of a line. It is used in various disciplines, such as physics and economics, to model relationships and predict trends. In education, mastering this concept is crucial for students as it forms the basis for graphing linear equations and understanding the behavior of lines in a coordinate plane. |
Slope |

|
Definition--Slope Concepts--Undefined Slope | Undefined SlopeTopicSlope DefinitionUndefined slope occurs when a vertical line is present, meaning there is no change in x. DescriptionAn undefined slope is a critical concept in mathematics, particularly in graphing. It indicates a vertical line where the change in x is zero, making the slope calculation impossible. This concept is important in various fields, such as computer graphics and data analysis, where vertical lines can represent boundaries or limits. Understanding undefined slopes helps students in identifying and interpreting vertical lines in graphs. |
Slope |

|
Definition--Slope Concepts--Undefined Slope | Undefined SlopeTopicSlope DefinitionUndefined slope occurs when a vertical line is present, meaning there is no change in x. DescriptionAn undefined slope is a critical concept in mathematics, particularly in graphing. It indicates a vertical line where the change in x is zero, making the slope calculation impossible. This concept is important in various fields, such as computer graphics and data analysis, where vertical lines can represent boundaries or limits. Understanding undefined slopes helps students in identifying and interpreting vertical lines in graphs. |
Slope |

|
Definition--Slope Concepts--Undefined Slope | Undefined SlopeTopicSlope DefinitionUndefined slope occurs when a vertical line is present, meaning there is no change in x. DescriptionAn undefined slope is a critical concept in mathematics, particularly in graphing. It indicates a vertical line where the change in x is zero, making the slope calculation impossible. This concept is important in various fields, such as computer graphics and data analysis, where vertical lines can represent boundaries or limits. Understanding undefined slopes helps students in identifying and interpreting vertical lines in graphs. |
Slope |

|
Definition--Slope Concepts--Zero Slope | Zero SlopeTopicSlope DefinitionZero slope describes a horizontal line where there is no change in y as x changes. DescriptionA zero slope is a key concept in algebra and geometry, representing a horizontal line. It is used in various applications, such as designing flat surfaces and analyzing constant relationships in data. In education, understanding zero slopes helps students in graphing and interpreting horizontal lines, enhancing their ability to analyze linear relationships. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Zero Slope | Zero SlopeTopicSlope DefinitionZero slope describes a horizontal line where there is no change in y as x changes. DescriptionA zero slope is a key concept in algebra and geometry, representing a horizontal line. It is used in various applications, such as designing flat surfaces and analyzing constant relationships in data. In education, understanding zero slopes helps students in graphing and interpreting horizontal lines, enhancing their ability to analyze linear relationships. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Definition--Slope Concepts--Zero Slope | Zero SlopeTopicSlope DefinitionZero slope describes a horizontal line where there is no change in y as x changes. DescriptionA zero slope is a key concept in algebra and geometry, representing a horizontal line. It is used in various applications, such as designing flat surfaces and analyzing constant relationships in data. In education, understanding zero slopes helps students in graphing and interpreting horizontal lines, enhancing their ability to analyze linear relationships. For a complete collection of terms related to Slope click on this link: Slope Collection. |
Slope |

|
Desmos Activity: Exploring the Slope Formula | Desmos Activity: Exploring the Slope Formula
Click on this link to see the complete collection of Desmos resources.
Use a custom Desmos graphing calculator activity to explore the slope formula. The Desmos activity includes the slope formula equation. Students input the values for the two coordinates. They can also use the provided sliders to input the values. The Desmos interactive will calculate the slope of the line connecting the two points, as well as the graph of the line itself. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. |
Slope |

|
Desmos Activity: Exploring the Slope Formula | Desmos Activity: Exploring the Slope Formula
Click on this link to see the complete collection of Desmos resources.
Use a custom Desmos graphing calculator activity to explore the slope formula. The Desmos activity includes the slope formula equation. Students input the values for the two coordinates. They can also use the provided sliders to input the values. The Desmos interactive will calculate the slope of the line connecting the two points, as well as the graph of the line itself. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. |
Slope |

|
Desmos Activity: Exploring the Slope Formula | Desmos Activity: Exploring the Slope Formula
Click on this link to see the complete collection of Desmos resources.
Use a custom Desmos graphing calculator activity to explore the slope formula. The Desmos activity includes the slope formula equation. Students input the values for the two coordinates. They can also use the provided sliders to input the values. The Desmos interactive will calculate the slope of the line connecting the two points, as well as the graph of the line itself. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. |
Slope |

|
Desmos Activity: Exploring the Slope Formula | Desmos Activity: Exploring the Slope Formula
Click on this link to see the complete collection of Desmos resources.
Use a custom Desmos graphing calculator activity to explore the slope formula. The Desmos activity includes the slope formula equation. Students input the values for the two coordinates. They can also use the provided sliders to input the values. The Desmos interactive will calculate the slope of the line connecting the two points, as well as the graph of the line itself. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. |
Slope |

|
Desmos Activity: Exploring the Slope Formula | Desmos Activity: Exploring the Slope Formula
Click on this link to see the complete collection of Desmos resources.
Use a custom Desmos graphing calculator activity to explore the slope formula. The Desmos activity includes the slope formula equation. Students input the values for the two coordinates. They can also use the provided sliders to input the values. The Desmos interactive will calculate the slope of the line connecting the two points, as well as the graph of the line itself. There is a companion worksheet for this activity, which subscribers can download. The worksheet is a PDF file. |
Slope |

|
Desmos Activity: Slope As Rate of Change | Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost. |
Slope and Ratios and Rates |

|
Desmos Activity: Slope As Rate of Change | Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost. |
Slope and Ratios and Rates |

|
Desmos Activity: Slope As Rise Over Run | Desmos Activity: Slope As Rise Over Run This Desmos activity allows students to explore slope as the ratio of the rise over the run. Click Preview to launch the activity. In the activity students click on the points to create a line segment connecting two points. Use the background grid to determine the rise and the run and calculate the slope. |
Slope |

|
Desmos Activity: Slope As Rise Over Run | Desmos Activity: Slope As Rise Over Run This Desmos activity allows students to explore slope as the ratio of the rise over the run. Click Preview to launch the activity. In the activity students click on the points to create a line segment connecting two points. Use the background grid to determine the rise and the run and calculate the slope. |
Slope |

|
Desmos Activity: Slope As Rise Over Run | Desmos Activity: Slope As Rise Over Run This Desmos activity allows students to explore slope as the ratio of the rise over the run. Click Preview to launch the activity. In the activity students click on the points to create a line segment connecting two points. Use the background grid to determine the rise and the run and calculate the slope. |
Slope |

|
Desmos Activity: Slope As Rise Over Run 2 | Desmos Activity: Slope As Rise Over Run 2 In this activity, students input different values for the coordinates to create a new line. They can then measure the rise and run to calculate the slope. |
Slope |

|
Desmos Activity: Slope As Rise Over Run 2 | Desmos Activity: Slope As Rise Over Run 2 In this activity, students input different values for the coordinates to create a new line. They can then measure the rise and run to calculate the slope. |
Slope |