IXL Ad

Illustrative Math-Media4Math Alignment

 

 

Illustrative Math Alignment: Grade 8 Unit 3

Linear Relationships

Lesson 8: Translating to y = mx + b

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image Title Body Curriculum Topic
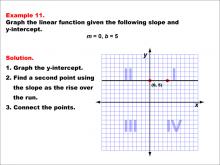
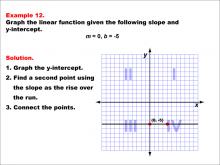
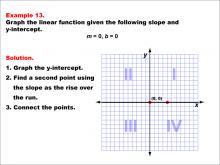
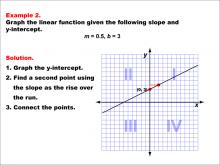
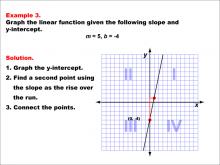
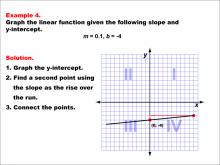
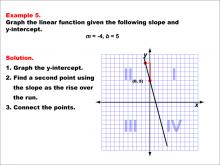
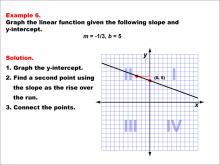
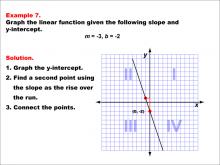
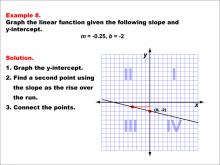
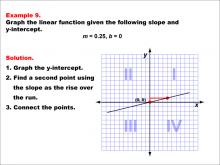
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13

Topic

Linear Functions

Description

This example illustrates the process of converting the linear equation -x + y = 1 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = x + 1. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -x - y = -1 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -x + 1. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15

Topic

Linear Functions

Description

This example showcases the transformation of the linear equation -x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y, resulting in y = -x - 1. This step-by-step conversion clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line.

Linear functions are fundamental mathematical concepts that describe relationships between two variables. The examples in this collection, such as showing step-by-step transformations from standard form to slope-intercept form, help in understanding how each part of the equation affects the graph and the relationship itself.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17

Topic

Linear Functions

Description

This example illustrates the conversion of the linear equation x - y = -1 from standard form to slope-intercept form. The solution involves isolating y, resulting in y = x + 1. This process clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -x - y = 1 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = -x - 1. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19

Topic

Linear Functions

Description

This example illustrates the conversion of the linear equation 12x + 28y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -3/7 x. This process clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2

Topic

Linear Functions

Description

This example illustrates the conversion of the linear equation 3x + 6y = -18 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -1/2 x - 3. This process clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -14x - 35y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = -2/5 x. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21

Topic

Linear Functions

Description

This example showcases the transformation of the linear equation 28x - 21y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 4/3 x. This step-by-step solution clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22

Topic

Linear Functions

Description

This example illustrates the conversion of the linear equation -13x + 39y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = 1/3 x. This process clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3

Topic

Linear Functions

Description

This example showcases the transformation of the linear equation 5x - 2y = 12 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 2.5x - 6. This step-by-step solution clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -6x + 10y = 20 from standard form to slope-intercept form. The solution process involves isolating y and dividing by its coefficient, resulting in y = 0.6x + 2. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5

Topic

Linear Functions

Description

This example illustrates the process of converting the linear equation -9x - 15y = -45 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = 3/5 x + 3. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6

Topic

Linear Functions

Description

This example demonstrates the conversion of the linear equation -8x - 12y = 25 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -2/3 x - 25/12. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7

Topic

Linear Functions

Description

This example illustrates the transformation of the linear equation -2x + 16y = -36 from standard form to slope-intercept form. The solution process involves solving for y, resulting in y = 1/8 x - 9/4. This step-by-step conversion clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8

Topic

Linear Functions

Description

This example showcases the conversion of the linear equation -7x + 21y = 63 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = 1/3 x + 3. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9 Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9

Topic

Linear Functions

Description

This example demonstrates the process of converting the linear equation 10x - 28y = 56 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = (5/14)x - 2. This transformation clearly reveals the slope and y-intercept of the line.

 Standard Form
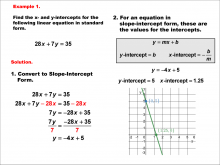
Math Example--Linear Function Concepts--Linear Intercepts: Example 1 Math Example--Linear Function Concepts--Linear Intercepts: Example 1 Math Example--Linear Function Concepts--Linear Intercepts: Example 1

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
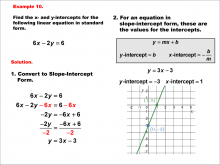
Math Example--Linear Function Concepts--Linear Intercepts: Example 10 Math Example--Linear Function Concepts--Linear Intercepts: Example 10 Math Example--Linear Function Concepts--Linear Intercepts: Example 10

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
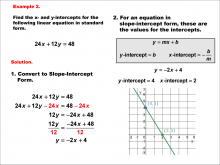
Math Example--Linear Function Concepts--Linear Intercepts: Example 2 Math Example--Linear Function Concepts--Linear Intercepts: Example 2 Math Example--Linear Function Concepts--Linear Intercepts: Example 2

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
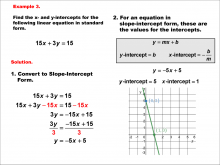
Math Example--Linear Function Concepts--Linear Intercepts: Example 3 Math Example--Linear Function Concepts--Linear Intercepts: Example 3 Math Example--Linear Function Concepts--Linear Intercepts: Example 3

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
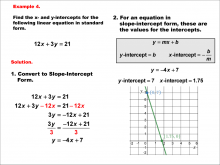
Math Example--Linear Function Concepts--Linear Intercepts: Example 4 Math Example--Linear Function Concepts--Linear Intercepts: Example 4 Math Example--Linear Function Concepts--Linear Intercepts: Example 4

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
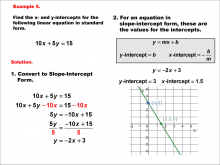
Math Example--Linear Function Concepts--Linear Intercepts: Example 5 Math Example--Linear Function Concepts--Linear Intercepts: Example 5 Math Example--Linear Function Concepts--Linear Intercepts: Example 5

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
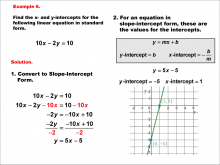
Math Example--Linear Function Concepts--Linear Intercepts: Example 6 Math Example--Linear Function Concepts--Linear Intercepts: Example 6 Math Example--Linear Function Concepts--Linear Intercepts: Example 6

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
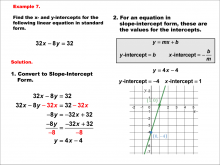
Math Example--Linear Function Concepts--Linear Intercepts: Example 7 Math Example--Linear Function Concepts--Linear Intercepts: Example 7 Math Example--Linear Function Concepts--Linear Intercepts: Example 7

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
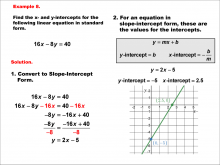
Math Example--Linear Function Concepts--Linear Intercepts: Example 8 Math Example--Linear Function Concepts--Linear Intercepts: Example 8 Math Example--Linear Function Concepts--Linear Intercepts: Example 8

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
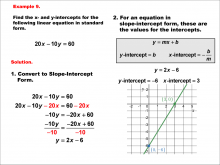
Math Example--Linear Function Concepts--Linear Intercepts: Example 9 Math Example--Linear Function Concepts--Linear Intercepts: Example 9 Math Example--Linear Function Concepts--Linear Intercepts: Example 9

This is part of a collection of math examples that focus on linear function concepts.

 Slope-Intercept Form and Standard Form
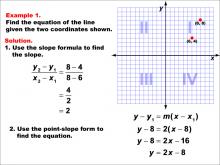
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
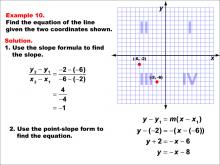
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
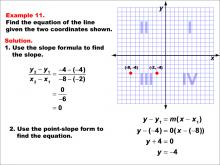
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 11 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 11 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 11

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
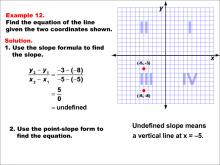
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 12 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 12 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 12

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
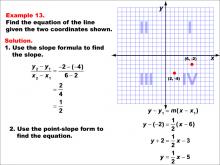
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
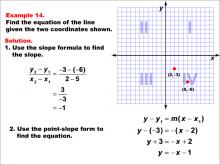
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
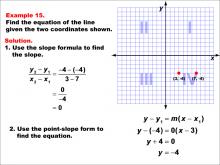
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29

This is part of a collection of math examples that focus on linear function concepts.

 Point-Slope Form and Slope-Intercept Form