
Illustrative Math Alignment: Grade 8 Unit 3
Linear Equations and Linear Systems
Lesson 1: Number Puzzles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 5 | Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 5
In this video learn the mechanics of solving a two-step equation involving addition and multiplication. In this variation, the x-term has a negative coefficient. . |
Solving Two-Step Equations |

|
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 6 | Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 6
In this video learn the mechanics of solving a two-step equation involving addition and multiplication. In this variation, the x-term has a negative coefficient and the term on the other side of the equals sign is negative. . |
Solving Two-Step Equations |

|
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 7 | Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 7
In this video learn the mechanics of solving a two-step equation involving subtraction and multiplication. In this variation, the x-term has a negative coefficient. . |
Solving Two-Step Equations |

|
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 8 | Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 8
In this video learn the mechanics of solving a two-step equation involving subtraction and multiplication. In this variation, the x-term has a negative coefficient and the term on the other side of the equals sign is negative. . |
Solving Two-Step Equations |

|
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 9 | Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 9
In this video learn the mechanics of solving a two-step equation involving addition and division. . |
Solving Two-Step Equations |

|
Closed Captioned Video: One-Step Equations: Addition | Closed Captioned Video: One-Step Equations: Addition
Video Tutorial: One-Step Equations: Addition. In this video, get an overview of one-step equations and how to solve them. In particular, look at one-step addition equations. |
Solving One-Step Equations |

|
Closed Captioned Video: One-Step Equations: Division | Closed Captioned Video: One-Step Equations: Division
Video Tutorial: One-Step Equations: Division. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step division equations. |
Solving One-Step Equations |

|
Closed Captioned Video: One-Step Equations: Multiplication | Closed Captioned Video: One-Step Equations: Multiplication
Video Tutorial: One-Step Equations: Multiplication. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step multiplication equations. |
Solving One-Step Equations |

|
Closed Captioned Video: One-Step Equations: Subtraction | Closed Captioned Video: One-Step Equations: Subtraction
Video Tutorial: One-Step Equations: Subtraction. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step subtraction equations. |
Solving One-Step Equations |

|
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negative
Video Tutorial: The Distributive Property: a(-x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x + b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positive
Video Tutorial: The Distributive Property: a(-x + b), a negative, b positive. In this video use the distributive property with an expression of the form a(-x + b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x + b), all constants positive | Closed Captioned Video: The Distributive Property: a(-x + b), all constants positive
Video Tutorial: The Distributive Property: a(-x + b), all constants positive. In this video use the distributive property with an expression of the form a(-x + b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negative
Video Tutorial: The Distributive Property: a(-x - b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x - b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positive
Video Tutorial: The Distributive Property: a(-x - b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(-x - b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), all constants positive | Closed Captioned Video: The Distributive Property: a(-x - b), all constants positive
Video Tutorial: The Distributive Property: a(-x - b), all constants positive. In this video use the distributive property with an expression of the form a(-x - b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positive | Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positive
Video Tutorial: The Distributive Property: a(bx + c), a negative, b and c positive. In this video, we will use the distributive property with an expression of the form a(bx + c), a negative, b and c positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), all constants negative | Closed Captioned Video: The Distributive Property: a(bx + c), all constants negative
Video Tutorial: The Distributive Property: a(bx + c), all constants negative. In this video use the distributive property with an expression of the form a(bx + c), all negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), all constants positive | Closed Captioned Video: The Distributive Property: a(bx + c), all constants positive
Video Tutorial: The Distributive Property: a(bx + c), all constants positive. In this video use the distributive property with an expression of the form a(bx + c), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positive | Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positive
Video Tutorial: The Distributive Property: a(bx - c), a negative, b and c positive. In this video use the distributive property with an expression of the form a(bx - c), a negative, b and c positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), all constants negative | Closed Captioned Video: The Distributive Property: a(bx - c), all constants negative
Video Tutorial: The Distributive Property: a(bx - c), all constants negative. In this video, we will use the distributive property with an expression of the form a(bx - c), all negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), all constants positive | Closed Captioned Video: The Distributive Property: a(bx - c), all constants positive
Video Tutorial: The Distributive Property: a(bx - c), all constants positive. In this video use the distributive property with an expression of the form a(bx - c), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negative
Video Tutorial: The Distributive Property: a(x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(x + b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positive
Video Tutorial: The Distributive Property: a(x + b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(x + b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), all constants positive | Closed Captioned Video: The Distributive Property: a(x + b), all constants positive
Video Tutorial: The Distributive Property: a(x + b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x + b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negative
Video Tutorial: The Distributive Property: a(x - b), a negative, b negative. In this video, we will use the distributive property with an expression of the form a(x - b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positive
Video Tutorial: The Distributive Property: a(x - b), a negative, b positive. In this video use the distributive property with an expression of the form a(x - b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), all constants positive | Closed Captioned Video: The Distributive Property: a(x - b), all constants positive
Video Tutorial: The Distributive Property: a(x - b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x - b), all constants positive. |
Numerical and Algebraic Expressions |

|
Definition--Order of Operations | Definition--Order of Operations
Watch the following video on Order of Operations. (The transcript is included.) Video Transcript
A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division. Because addition is commutative, adding from left to right, or right to left, gives you the same result. The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations. Subtraction isn't commutative. |
Numerical Expressions and Variable Expressions |

|
Desmos Activity: Linear Equations in Point-Slope Form | In this graphing calculator activity, have your students explore how to convert linear equations in point-slope to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of coordinates of the point and the slope of the line. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link. |
Point-Slope Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |

|
Factor Bingo Game | A bingo-style game where students identify the factors of numbers I the range 1-20. Note: The download is a PDF file. Related ResourcesTo see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library |
Numerical and Algebraic Expressions |

|
Factor Table, 1-10 | A table that lists all the factors for the numbers 1-10. Note: The download is a PDF file. Related ResourcesTo see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library |
Numerical and Algebraic Expressions |

|
Factor Table, 1-20 | A table that lists all the factors for the numbers 1-20. Note: The download is a PDF file. Related ResourcesTo see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library |
Numerical and Algebraic Expressions |

|
Factor Table, 1-5 | A table that lists all the factors for the numbers 1-5. Note: The download is a PDF file. Related ResourcesTo see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library |
Numerical and Algebraic Expressions |
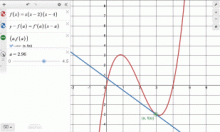
|
Instructional Resource | Instructional Resource | Using the Point-Slope Form in Calculus
In this tutorial, learn how to use the point-slope form to find the equation of the line tangent to a function at a given point. —Click on Preview to see the tutorial— |
Calculus Vocabulary |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + -b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |