
Illustrative Math Alignment: Grade 8 Unit 3
Linear Equations and Linear Systems
Lesson 4: More Balanced Moves
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Equation Concepts--Multiplication Property of Equality | Multiplication Property of EqualityTopicEquations DefinitionThe Multiplication Property of Equality states that if you multiply both sides of an equation by the same nonzero value, the equality remains true. DescriptionThe Multiplication Property of Equality is a fundamental principle in algebra. It states that for any real numbers a, b, and c (where 𝑐 ≠ 0), if a = b, then ac = bc This property is used to solve equations by isolating variables. For example, to solve x/3 = 4 you multiply both sides by 3 to get x = 12. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Nonlinear Equation | Nonlinear EquationTopicEquations DefinitionA nonlinear equation is an equation that graphs as a curve and does not form a straight line. DescriptionNonlinear equations are equations that involve variables raised to powers other than one or involve products of variables. For example, the equation y = x2 is nonlinear because it graphs as a parabola. These equations are used to model more complex relationships than linear equations. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Numerical Expression | Numerical ExpressionTopicEquations DefinitionA numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables. DescriptionNumerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 3 + 4 × 2 is a numerical expression. These expressions are evaluated to find their value. In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills. |
Numerical Expressions |

|
Definition--Equation Concepts--One-Step Equation | One-Step EquationTopicEquations DefinitionA one-step equation requires only one operation to solve. DescriptionOne-step equations are the simplest type of equations in algebra. They involve a single operation to isolate the variable. For example, solving x + 3 = 7 requires subtracting 3 from both sides to find x = 4. These equations are used in basic problem-solving scenarios and form the foundation for understanding more complex equations. Understanding one-step equations helps students develop confidence in solving algebraic problems and prepares them for advanced algebraic concepts. |
Solving One-Step Equations |

|
Definition--Equation Concepts--Polynomial Equation | Polynomial EquationTopicEquations DefinitionA polynomial equation is an equation that involves a polynomial expression. DescriptionPolynomial equations involve expressions that include terms with variables raised to whole-number exponents. For example, the equation x2 − 4x + 4 = 0 is a polynomial equation. These equations can be linear, quadratic, cubic, etc., depending on the highest power of the variable. |
Polynomial Functions and Equations |

|
Definition--Equation Concepts--Quadratic Equation | Quadratic EquationTopicEquations DefinitionA quadratic equation is a polynomial equation of degree 2, typically in the form ax2 + bx + c = 0. DescriptionQuadratic equations are fundamental in algebra and involve variables raised to the second power. For example, the equation x2 − 4x + 4 = 0 is quadratic. These equations can be solved using methods such as factoring, completing the square, and the quadratic formula. |
Quadratic Equations and Functions |

|
Definition--Equation Concepts--Reflexive Property of Equality | Reflexive Property of EqualityTopicEquations DefinitionThe Reflexive Property of Equality states that any value is equal to itself. DescriptionThe Reflexive Property of Equality is a basic principle in mathematics. It states that for any value a, a = a This property is used to justify steps in solving equations and proving mathematical statements. In real-world applications, the reflexive property underlies the concept of identity and is fundamental in logical reasoning and proofs. Understanding this property helps students build a strong foundation in algebra and develop rigorous mathematical arguments. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Right Side of the Equation | Right Side of the EquationTopicEquations DefinitionThe right side of the equation refers to the expression on the right side of the equals sign. DescriptionThe right side of an equation is the part of the equation that appears after the equals sign. For example, in the equation 2x + 3 = 7 the right side is 7. Understanding the right side of the equation is crucial for solving and balancing equations. |
Applications of Equations and Inequalities |
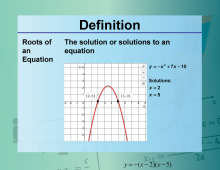
|
Definition--Equation Concepts--Roots of an Equation | Roots of an EquationTopicEquations DefinitionThe roots of an equation are the values of the variable that satisfy the equation. DescriptionThe roots of an equation are the solutions that make the equation true. For example, the roots of the quadratic equation x2 − 4x + 4 = 0 are x = 2 because substituting 2 into the equation satisfies it. Finding roots is a fundamental task in algebra. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Solution | SolutionTopicEquations DefinitionA solution is the value(s) of the variable(s) that satisfy an equation. DescriptionThe concept of solution is fundamental in equations, referring to the values that make the equation true. For example, in the equation x + 2 = 5 the solution is x = 3 because substituting 3 in place of x results in a true statement. Solutions can exist for various types of equations, whether single-variable, multi-variable, linear, or nonlinear. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Solving an Equation | Solving an EquationTopicEquations DefinitionSolving an equation involves finding the value(s) of the variable(s) that make the equation true. DescriptionSolving an equation is a key skill in algebra, where one determines the values of variables that satisfy the equation. For example, in the equation 2x + 3 = 7 one can find that x = 2 by isolating the variable through algebraic manipulations. Different techniques such as substitution, factoring, or using the quadratic formula may apply depending on the complexity of the equation. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Subtraction Property of Equality | Subtraction Property of EqualityTopicEquations DefinitionThe Subtraction Property of Equality states that if you subtract the same value from both sides of an equation, the equality remains true. DescriptionThe Subtraction Property of Equality is a fundamental principle in algebra. It states that for any real numbers a, b, and c, if a = b, then a − c = b − c This property is used to solve equations by isolating variables. For example, to solve x + 3 = 7 you subtract 3 from both sides to get x = 4. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Symmetric Property of Equality | Symmetric Property of EqualityTopicEquations DefinitionThe Symmetric Property of Equality states that if a = b, then b = a. DescriptionThe Symmetric Property of Equality is a basic principle in mathematics. It asserts that the equality relation is symmetric, meaning that if one quantity equals another, then the second quantity equals the first. For example, if x = y then y = x This property is used to justify steps in solving equations and proving mathematical statements. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--The Unknown | The UnknownTopicEquations DefinitionThe unknown is the variable in an equation that needs to be solved for. DescriptionThe unknown in an equation represents the value that needs to be determined. For example, in the equation x + 3 = 7 x is the unknown. Identifying and solving for the unknown is a core aspect of algebra. In real-world applications, finding the unknown is crucial for solving problems in various fields such as science, engineering, and finance. Understanding how to identify and solve for the unknown helps students develop problem-solving skills and apply mathematical concepts to real-life situations. |
Variables and Unknowns |

|
Definition--Equation Concepts--Transitive Property of Equality | Transitive Property of EqualityTopicEquations DefinitionThe Transitive Property of Equality states that if a = b and b = c, then a = c. DescriptionThe Transitive Property of Equality is a fundamental principle in mathematics. It states that if one quantity equals a second quantity, and the second quantity equals a third, then the first and third quantities are equal. For example, if x = y and y = z then x = z This property is used to justify steps in solving equations and proving mathematical statements. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--True Equation | True EquationTopicEquations DefinitionA true equation is an equation that holds true for the given values of the variable(s). DescriptionA true equation is an equation that is valid for specific values of the variable(s). For example, the equation 2 + 3 = 5 is true because both sides are equal. Identifying true equations is important in verifying the correctness of mathematical statements. In real-world applications, recognizing true equations helps in ensuring the accuracy of mathematical models and solutions. Understanding true equations helps students develop critical thinking and analytical skills. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Two-Step Equation | Two-Step EquationTopicEquations DefinitionA two-step equation requires two operations to solve. DescriptionTwo-step equations involve performing two operations to isolate the variable. For example, solving 2x + 3 = 7 requires subtracting 3 from both sides and then dividing by 2 to find x = 2. These equations are common in algebra and require a systematic approach to solve. In real-world applications, two-step equations are used in problem-solving scenarios such as calculating costs or determining measurements. Understanding how to solve two-step equations helps students develop critical thinking and problem-solving skills. |
Solving Two-Step Equations |

|
Definition--Equation Concepts--Variable Expression | Variable ExpressionTopicEquations DefinitionA variable expression is a mathematical phrase involving variables, numbers, and operation symbols. DescriptionVariable expressions consist of variables, numbers, and operations such as addition, subtraction, multiplication, and division. For example, 3x + 4 is a variable expression. These expressions are used to represent quantities and relationships in algebra. |
Variable Expressions |
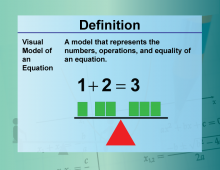
|
Definition--Equation Concepts--Visual Models for Equations | Visual Models for EquationsTopicEquations DefinitionVisual models for equations use graphical representations to illustrate the relationships between variables. DescriptionVisual models for equations include graphs, charts, and diagrams that represent the relationships between variables. For example, a graph of the equation y = 2x + 3 shows a straight line with a slope of 2 and a y-intercept of 3. These models help in understanding and interpreting equations. |
Applications of Equations and Inequalities |

|
Definition--Order of Operations | Definition--Order of Operations
Watch the following video on Order of Operations. (The transcript is included.) Video Transcript
A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division. Because addition is commutative, adding from left to right, or right to left, gives you the same result. The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations. Subtraction isn't commutative. |
Numerical Expressions and Variable Expressions |

|
Desmos Activity: Linear Equations in Point-Slope Form | In this graphing calculator activity, have your students explore how to convert linear equations in point-slope to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of coordinates of the point and the slope of the line. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link. |
Point-Slope Form |

|
Desmos Activity: Linear Equations in Standard Form | Desmos Activity: Linear Equations in Standard Form
In this graphing calculator activity, have your students explore how to convert linear equations in standard form to a linear function in slope-intercept form. This Desmos template allows students to explore the effect of changes in the values of A, B, and C in the standard form and m and b in the slope-intercept form. A companion downloadable worksheet uses the graphing calculator template to explore the properties of these linear equations and functions. Note: The download is a PDF worksheet. —PRESS PREVIEW TO SEE THE ACTIVITY— To see the complete collection of Desmos activities, click on this link.The following section includes background information on slope. This background also includes video resources and accompanying transcripts. |
Standard Form |
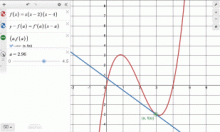
|
Instructional Resource | Instructional Resource | Using the Point-Slope Form in Calculus
In this tutorial, learn how to use the point-slope form to find the equation of the line tangent to a function at a given point. —Click on Preview to see the tutorial— |
Calculus Vocabulary |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + -b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + -b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax + b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX + By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX + By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax - b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: -ax - b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -AX - By = C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: -AX - By = C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx + c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 + bx - c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 + bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0 | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx + c = 0
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx + c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: -ax^2 - bx - c
In this PowerPoint presentation, analyze the steps in solving a quadratic equation with two roots. In this Interactive we work with this version of the quadratic equation: -ax^2 - bx - c = 0. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Polynomial Functions and Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = -cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = -cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = c | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = c
In this interactive, look at the solution to a two-step equation by clicking on various hot spots. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx + d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx + d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = cx + d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx - d | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: ax + b = cx - d
In this PowerPoint presentation, analyze the solution to a multi-step equation of the form: ax + b = cx - d. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Solving Two-Step Equations |

|
INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = -C | INSTRUCTIONAL RESOURCE: Anatomy of an Equation: AX + By = -C
In this PowerPoint Presentation, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this Interactive we work with this version of the Standard Form: AX + By = -C. This is part of a collection of tutorials for solving different types of equations. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Standard Form |