
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 16: Finding Cone Dimensions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Animated Math Clip Art--Equations--Solving One-Step Multiplication Equations 3 | Animated Math Clip Art--Equations--Solving One-Step Multiplication Equations 3TopicEquations DescriptionThis animated clip art illustrates the process of solving one-step multiplication equations. The animation demonstrates dividing both sides of the equation by the same value to isolate the variable, highlighting the concept of maintaining equation balance. This visual resource is effective for teaching the concept of solving equations. It helps students visualize the abstract process of balancing equations through a clear, step-by-step example. This clip art can be used in lessons to provide multiple perspectives on solving equations, enhancing understanding. |
Solving One-Step Equations |

|
Animated Math Clip Art--Equations--Solving One-Step Multiplication Equations 4 | Animated Math Clip Art--Equations--Solving One-Step Multiplication Equations 4TopicEquations DescriptionThis animated clip art illustrates the process of solving one-step multiplication equations. The animation demonstrates dividing both sides of the equation by the same value to isolate the variable, highlighting the concept of maintaining equation balance. This visual resource is effective for teaching the concept of solving equations. It helps students visualize the abstract process of balancing equations through a clear, step-by-step example. This clip art can be used in lessons to provide multiple perspectives on solving equations, enhancing understanding. |
Solving One-Step Equations |
|
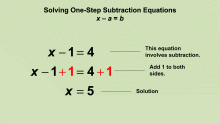
Animated Math Clip Art--Equations--Solving One-Step Subtraction Equations 1 | Animated Math Clip Art--Equations--Solving One-Step Division Equations 1TopicEquations DescriptionThis animated clip art demonstrates solving one-step division equations. The animation shows multiplying both sides of the equation by the same number to isolate the variable, emphasizing the principle of maintaining equation balance. This visual tool is valuable for teaching students the concept of solving equations. It helps students visualize the abstract process of balancing equations by providing a clear, step-by-step example. This clip art can be part of a comprehensive lesson plan that uses multiple animations to reinforce understanding. |
Solving One-Step Equations |

|
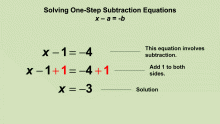
Animated Math Clip Art--Equations--Solving One-Step Subtraction Equations 2 | Animated Math Clip Art--Equations--Solving One-Step Division Equations 2TopicEquations DescriptionThis animated clip art demonstrates solving one-step division equations. The animation shows multiplying both sides of the equation by the same number to isolate the variable, emphasizing the principle of maintaining equation balance. This visual tool is valuable for teaching students the concept of solving equations. It helps students visualize the abstract process of balancing equations by providing a clear, step-by-step example. This clip art can be part of a comprehensive lesson plan that uses multiple animations to reinforce understanding. |
Solving One-Step Equations |
|
Animated Math Clip Art--Equations--Solving One-Step Subtraction Equations 3 | Animated Math Clip Art--Equations--Solving One-Step Division Equations 3TopicEquations DescriptionThis animated clip art demonstrates solving one-step division equations. The animation shows multplying both sides of the equation by the same number to isolate the variable, emphasizing the principle of maintaining equation balance. This visual tool is valuable for teaching students the concept of solving equations. It helps students visualize the abstract process of balancing equations by providing a clear, step-by-step example. This clip art can be part of a comprehensive lesson plan that uses multiple animations to reinforce understanding. |
Solving One-Step Equations |

|
Animated Math Clip Art--Equations--Solving One-Step Subtraction Equations 4 | Animated Math Clip Art--Equations--Solving One-Step Division Equations 4TopicEquations DescriptionThis animated clip art demonstrates solving one-step division equations. The animation shows multiplying both sides of the equation by the same number to isolate the variable, emphasizing the principle of maintaining equation balance. This visual tool is valuable for teaching students the concept of solving equations. It helps students visualize the abstract process of balancing equations by providing a clear, step-by-step example. This clip art can be part of a comprehensive lesson plan that uses multiple animations to reinforce understanding. |
Solving One-Step Equations |

|
Closed Captioned Video: Linear Inequality | Closed Captioned Video: Linear Inequality
In this TI Nspire tutorial, the Graph window is used to graph a linear inequality. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Inequalities |

|
Closed Captioned Video: Linear Inequality Using Sliders | Closed Captioned Video: Linear Inequality Using Sliders
In this TI Nspire tutorial, the Graph window is used to graph a linear inequality in slope-intercept form using sliders. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. |
Inequalities |

|
Closed Captioned Video: Quadratic Inequality | Closed Captioned Video: Quadratic Inequality
In this TI Nspire tutorial for the TI-Nspire CAS, the Graph Window is used to graph quadratic inequalities. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Inequalities |

|
Closed Captioned Video: Algebra Applications: Inequalities | Closed Captioned Video: Algebra Applications: InequalitiesTopicInequalities |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Applications: Inequalities, 1 | Closed Captioned Video: Algebra Applications: Inequalities, 2TopicInequalities DescriptionThis video models an inequality to explain how floodgates in Venice prevent flooding during storms. The key concept is the activation threshold, where the water level exceeds a critical value. Vocabulary includes inequality, threshold, variable, and model. Using a TI-Nspire, the video demonstrates creating a random variable for water levels and a function to evaluate if floodgates should activate. It illustrates real-world applications in engineering and environmental management. |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Applications: Inequalities, 2 | Closed Captioned Video: Algebra Applications: Inequalities, 1TopicInequalities |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Nspirations: Inequalities | Closed Captioned Video: Algebra Nspirations: Inequalities
Used in just about any industry, inequalities, like equations, are fundamental building blocks of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video explores inequalities—concepts, properties, solutions, and notations— connects them to real-world contexts, and uses the TI-Nspire to make the algebra meaningful. The focus of this program is on linear inequalities in one and two variables. Concepts explored: Equations, inequalities. |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Nspirations: Inequalities, 1 | Closed Captioned Video: Algebra Nspirations: Inequalities, Segment 1
In this Investigation we explore linear inequalities in one variable. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Inequalities. Segments 1 and 2 are grouped together. |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Nspirations: Inequalities, 3 | Closed Captioned Video: Algebra Nspirations: Inequalities, Segment 3
In this Investigation we look at linear inequalities in two variables. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Inequalities. Segments 3 and 4 are grouped together. |
Applications of Equations and Inequalities and Inequalities |

|
Closed Captioned Video: Algebra Tiles: Adding Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Adding Integers Using Algebra Tiles
Video Tutorial: Algebra Tiles: Adding Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to add integers using algebra tiles. DescriptionVideo Tutorial: Algebra Tiles: Dividing Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to divide integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Dividing Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Dividing Integers Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Dividing Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to divide integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Equations Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Equations Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model equations using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Multi-Step Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Multi-Step Equations Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Multi-Step Equations Using Algebra Tiles. In this tutorial, students review the basics of how to use algebra tiles to model equations. Then the video focuses on how to model multi-step equations using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Negative Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Negative Integers Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Negative Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model negative integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling One-Step Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling One-Step Equations Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling One-Step Equations Using Algebra Tiles. In this tutorial, review the basics of how to use algebra tiles to model equations. Then the video focuses on how to model one-step equations using algebra tiles. —CLICK PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of the video tutorials on this topic, click on this link.The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Positive Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Positive Integers Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Positive Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model positive integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Quadratic Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Quadratic Equations Using Algebra Tiles
Video Tutorial: Algebra Tiles: Modeling Quadratic Equations Using Algebra Tiles. In this tutorial, review the basics of how to use algebra tiles to model equations. Then the video focuses on how to model quadratic equations using algebra tiles. DescriptionVideo Tutorial: Algebra Tiles: Dividing Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to divide integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Variable Expressions Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Variable Expressions Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Variable Expressions Using Algebra Tiles. In this tutorial, students review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model variable expressions using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Variables Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Variables Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Variables Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model variables using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Modeling Zero Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Modeling Zero Using Algebra Tiles
DescriptionVideo Tutorial: Algebra Tiles: Modeling Zero Using Algebra Tiles. In this tutorial, students review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to model zero using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Multiplying Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Multiplying Integers Using Algebra Tiles
DescriptionThis is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. —CLICK PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of the video tutorials on this topic, click on this link.The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Simplifying Variable Expressions Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Simplifying Variable Expressions Using Algebra Tiles
DescriptionThis is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. —CLICK PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of the video tutorials on this topic, click on this link.The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles
Video Tutorial: Algebra Tiles: Solving Multi-Step Equations Using Algebra Tiles. In this tutorial, students review how to model equations with algebra tiles. Then the video focuses on how to solve multi-step equations with algebra tiles. DescriptionThis is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Solving One-Step Equations Using Algebra Tiles
DescriptionThis is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. —CLICK PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of the video tutorials on this topic, click on this link.The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: Subtracting Integers Using Algebra Tiles | Closed Captioned Video: Algebra Tiles: Subtracting Integers Using Algebra Tiles
Video Tutorial: Algebra Tiles: Subtracting Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to subtract integers using algebra tiles. DescriptionVideo Tutorial: Algebra Tiles: Dividing Integers Using Algebra Tiles. In this tutorial, review the basic definition of what algebra tiles are and how they are used. Then the video focuses on how to divide integers using algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Algebra Tiles: What Are Algebra Tiles? | Closed Captioned Video: Algebra Tiles: What Are Algebra Tiles?
DescriptionVideo Tutorial: Algebra Tiles: What Are Algebra Tiles? In this tutorial, learn the basics of what algebra tiles are and how they are used. Use this video segment when first introducing algebra tiles. This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction. |
Algebra Tiles--Expressions and Equations |

|
Closed Captioned Video: Exp the Slope-Intercept form | Closed Captioned Video: Exp the Slope-Intercept form
In this TI Nspire tutorial, the Graph window is used to create a slider-based graph of a linear function in slope-intercept form. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Slope-Intercept Form |

|
Closed Captioned Video: Geometry Applications: 3D Geometry | Closed Captioned Video: Geometry Applications: 3D GeometryTopic3D Geometry |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 1 | Closed Captioned Video: Geometry Applications: 3D Geometry, 1Topic3D Geometry DescriptionDescription: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 2 | Closed Captioned Video: Geometry Applications: 3D Geometry, 2Topic3D Geometry DescriptionDescription: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences. |
3-Dimensional Figures, Pyramids and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 3 | Closed Captioned Video: Geometry Applications: 3D Geometry, 3Topic3D Geometry DescriptionDescription: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency. |
3-Dimensional Figures, Cylinders and Applications of 3D Geometry |

|
Closed Captioned Video: Slope of a Line Connecting Two Points | Closed Captioned Video: Slope of a Line Connecting Two Points
In this TI Nspire tutorial, the Graph window is to find the slope of two points connected by a line. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Slope |

|
Definition--Equation Concepts--"Not Equal To" | Not Equal ToTopicEquations DefinitionThe "Not Equal To" symbol (≠) is used to indicate that two values are not equal. DescriptionThe "Not Equal To" symbol is crucial in mathematics as it denotes inequality between two expressions. This symbol is used in various mathematical contexts, such as solving inequalities, comparing numbers, and expressing conditions in algebraic equations. For example, in the inequality 𝑥 ≠ 5, it means that x can be any number except 5. |
Numerical and Algebraic Expressions |

|
Definition--Equation Concepts--Addition Property of Equality | Addition Property of EqualityTopicEquations DefinitionThe Addition Property of Equality states that if you add the same value to both sides of an equation, the equality remains true. DescriptionThe Addition Property of Equality is a fundamental principle in algebra. It asserts that for any real numbers a, b, and c, if a = b, then a + c = b + c. This property is used to solve equations and maintain balance. For example, to solve x − 3 = 7, you add 3 to both sides to get x = 10. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Algebraic Equation | Algebraic EquationTopicEquations DefinitionAn algebraic equation is a mathematical statement that shows the equality of two algebraic expressions. It's also another way of referring to a polynomial equation. DescriptionAlgebraic equations are central to algebra and involve variables, constants, and arithmetic operations. They are used to represent relationships and solve problems. For instance, the equation 2x + 3 = 7 can be solved to find x. Algebraic equations come in various forms, including linear, quadratic, and polynomial equations. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Algebraic Expression | Algebraic ExpressionTopicEquations DefinitionAn algebraic expression is a combination of variables, constants, and arithmetic operations, without an equality sign. DescriptionAlgebraic expressions are fundamental components of algebra. They represent quantities and relationships without asserting equality. Examples include 3x + 4 and 5y − 2. Unlike equations, expressions cannot be solved but can be simplified or evaluated for given variable values. |
Numerical and Algebraic Expressions |

|
Definition--Equation Concepts--Assigning Values to Variables | Assigning Values to VariablesTopicEquations DefinitionAssigning values to variables involves giving specific values to variables in an equation or expression. DescriptionAssigning values to variables is a fundamental process in algebra. It involves substituting variables with specific numbers to evaluate expressions or solve equations. For example, in the equation y = 2x + 3 assigning x = 4 gives y = 11. |
Variable Expressions |

|
Definition--Equation Concepts--Conditional Equation | Conditional EquationTopicEquations DefinitionA conditional equation is true only for specific values of the variable(s). DescriptionConditional equations are equations that hold true only under certain conditions or for specific variable values. For example, the equation x2 = 4 is true only when x = 2 or x = −2. These equations contrast with identities, which are true for all variable values. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Constant Term | Constant TermTopicEquations DefinitionA constant term is a term in an algebraic expression that does not contain any variables. DescriptionConstant terms are fixed values in algebraic expressions and equations. They do not change because they lack variables. For example, in the expression 3x + 4 the number 4 is a constant term. Constant terms are essential in forming and solving equations. |
Variables and Unknowns |

|
Definition--Equation Concepts--Division Property of Equality | Division Property of EqualityTopicEquations DefinitionThe Division Property of Equality states that if you divide both sides of an equation by the same nonzero value, the equality remains true. DescriptionThe Division Property of Equality is a key principle in algebra. It states that for any real numbers a, b, and c (where 𝑐 ≠ 0), if a = b, then a ÷ c = b ÷ c This property is used to solve equations by isolating variables. For example, to solve 3x = 12 divide both sides by 3 to get x = 4. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Equality | EqualityTopicEquations DefinitionEquality is a mathematical statement that asserts that two expressions are equal. DescriptionEquality is a foundational concept in mathematics. It indicates that two expressions have the same value, represented by the symbol "=". For example, in the equation 2 + 3 = 5, both sides are equal. Equality is used to form equations and solve problems. In real-world applications, equality is used in accounting, engineering, and data analysis to ensure balance and accuracy. Understanding equality helps students develop logical reasoning and problem-solving skills. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Equation | EquationTopicEquations DefinitionAn equation is a mathematical statement that asserts the equality of two expressions. DescriptionEquations are central to mathematics, representing relationships between quantities. They consist of two expressions separated by an equals sign. For example, 2x + 3 = 7 is an equation that can be solved to find x. Equations can be linear, quadratic, or polynomial, among others. |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Equations in One Variable | Equations in One VariableTopicEquations DefinitionEquations in one variable involve a single variable and can be solved to find its value. DescriptionEquations in one variable are fundamental in algebra. They typically take the form of ax + b = 0, where x is the variable. Solving these equations involves isolating the variable to determine its value. For example, solving 2x + 3 = 7 yields x = 2 |
Applications of Equations and Inequalities |

|
Definition--Equation Concepts--Equations in Two Variables | Equations in Two VariablesTopicEquations DefinitionEquations in two variables involve two variables and describe a relationship between them. DescriptionEquations in two variables are essential in algebra and coordinate geometry. They typically take the form of ax + by = c and represent lines in a coordinate plane. For example, the equation 2x + 3y = 6 can be graphed as a line. |
Applications of Equations and Inequalities |