
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 16: Finding Cone Dimensions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
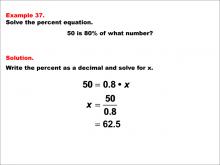
|
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
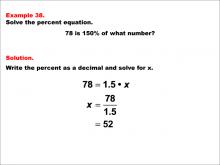
|
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
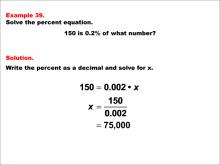
|
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
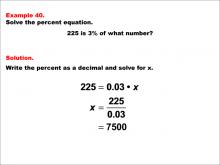
|
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |
|
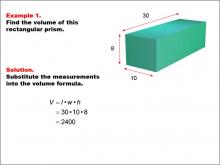
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
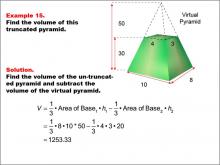
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
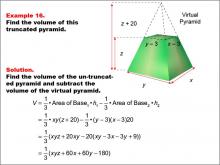
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |
|
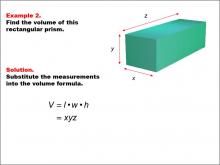
Math Example--Volume Concepts--Calculating Volume: Example 2 | Math Example--Volume Concepts--Calculating Volume: Example 2TopicVolume DescriptionA rectangular prism with dimensions labeled as x, y, and z. The image shows a general example of calculating the volume of a rectangular prism using variables instead of specific numbers. This image illustrates Example 2: The caption describes how to find the volume of a rectangular prism using variables for length (x), width (y), and height (z). The formula is given as V = x * y * z, but no specific values are provided. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 4 | Math Example--Volume Concepts--Calculating Volume: Example 4TopicVolume DescriptionA hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2). |
Volume |
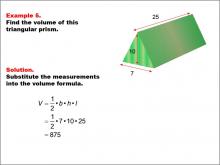
|
Math Example--Volume Concepts--Calculating Volume: Example 5 | Math Example--Volume Concepts--Calculating Volume: Example 5TopicVolume DescriptionThe image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875. |
Volume |
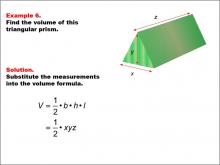
|
Math Example--Volume Concepts--Calculating Volume: Example 6 | Math Example--Volume Concepts--Calculating Volume: Example 6TopicVolume DescriptionThe image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 7 | Math Example--Volume Concepts--Calculating Volume: Example 7TopicVolume DescriptionThe image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 8 | Math Example--Volume Concepts--Calculating Volume: Example 8TopicVolume DescriptionThis image shows a hollow triangular prism with outer dimensions labeled as x, y, and z, and inner dimensions reduced by 2 units each. It demonstrates how to calculate the volume by subtracting the hollow region from the full prism. This image illustrates Example 8: "Find the volume of this hollow triangular prism." The solution uses V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = z(xy - (x - 2)(y - 2)) = z(x + y - 2).. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 9 | Math Example--Volume Concepts--Calculating Volume: Example 9TopicVolume Description
A green cylinder with a radius of 10 units and a height of 8 units. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 9: The task is to find the volume of the cylinder. The volume formula V = πr2h is used. Substituting the values r = 10 and h = 8, the volume is calculated as V= 800π. |
Volume |

|
Math Example: Algebra Tiles: Example 1 | Math Example: Algebra Tiles: Example 1TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the addition of 7 and 12 using algebra tiles. Two groups of yellow tiles, one with 7 tiles and another with 12 tiles, are combined to show a total of 19 tiles. This visual representation helps students understand the concept of addition with positive integers. |
Numerical Expressions |
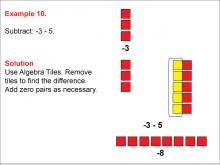
|
Math Example: Algebra Tiles: Example 10 | Math Example: Algebra Tiles: Example 10TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the subtraction of 5 from -3 using algebra tiles. The image shows 3 red tiles representing -3, and 5 yellow tiles are added to create zero pairs. After removing the zero pairs, 2 additional red tiles remain, illustrating that -3 - 5 = -8. |
Algebra Tiles--Expressions and Equations |
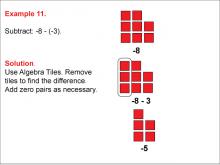
|
Math Example: Algebra Tiles: Example 11 | Math Example: Algebra Tiles: Example 11TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the subtraction of -3 from -8 using algebra tiles. The image shows 8 red tiles representing -8, and 3 red tiles are removed to demonstrate the subtraction of -3. The result is 5 red tiles, visually showing that -8 - (-3) = -5. |
Algebra Tiles--Expressions and Equations |
|
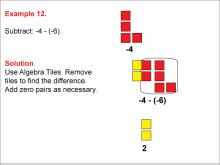
Math Example: Algebra Tiles: Example 12 | Math Example: Algebra Tiles: Example 12TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates the subtraction of -6 from -4 using algebra tiles. The image shows 4 red tiles representing -4, and 6 yellow tiles are added to form zero pairs. After removing these pairs, 2 yellow tiles remain, illustrating that -4 - (-6) = 2. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 13 | Math Example: Algebra Tiles: Example 13TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the subtraction of -7 from -7 using algebra tiles. The image shows 7 red tiles representing -7, and 7 red tiles are removed to demonstrate the subtraction of -7. The result is zero tiles remaining, visually showing that -7 - (-7) = 0. |
Algebra Tiles--Expressions and Equations |
|
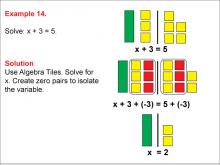
Math Example: Algebra Tiles: Example 14 | Math Example: Algebra Tiles: Example 14TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 3 = 5 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By creating zero pairs and isolating the variable, the solution x = 2 is visually represented. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 15 | Math Example: Algebra Tiles: Example 15TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + 4 = 2 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, the solution x = -2 is visually demonstrated. |
Algebra Tiles--Expressions and Equations |
|
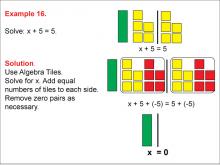
Math Example: Algebra Tiles: Example 16 | Math Example: Algebra Tiles: Example 16TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 5 = 5 using algebra tiles. The image shows green tiles representing the variable x, and yellow tiles representing positive integers. By manipulating the tiles, students can visually see that x = 0. |
Algebra Tiles--Expressions and Equations |
|
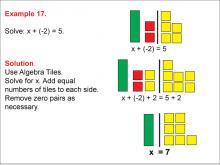
Math Example: Algebra Tiles: Example 17 | Math Example: Algebra Tiles: Example 17TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + (-2) = 5 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By strategically moving pieces and creating zero pairs, students can visually determine that x = 7. |
Algebra Tiles--Expressions and Equations |

|
Math Example: Algebra Tiles: Example 18 | Math Example: Algebra Tiles: Example 18TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + 3 = -2 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually see that x = -5. |
Algebra Tiles--Expressions and Equations |
|
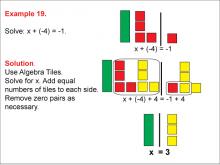
Math Example: Algebra Tiles: Example 19 | Math Example: Algebra Tiles: Example 19TopicNumerical and Algebraic Expressions DescriptionThis example illustrates solving the equation x + (-4) = -1 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually determine that x = 3. |
Algebra Tiles--Expressions and Equations |
|
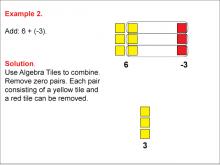
Math Example: Algebra Tiles: Example 2 | Math Example: Algebra Tiles: Example 2TopicNumerical and Algebraic Expressions DescriptionThis example illustrates the addition of 6 and -3 using algebra tiles. It shows 6 yellow tiles representing positive integers and 3 red tiles representing negative integers. After removing zero pairs (one yellow tile cancels out one red tile), the result is 3 yellow tiles, demonstrating that 6 + (-3) = 3. |
Algebra Tiles--Expressions and Equations |
|
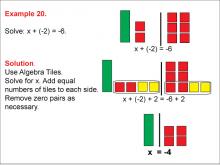
Math Example: Algebra Tiles: Example 20 | Math Example: Algebra Tiles: Example 20TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x + (-2) = -6 using algebra tiles. The image shows green tiles representing the variable x, yellow tiles representing positive integers, and red tiles representing negative integers. By manipulating the tiles and creating zero pairs, students can visually see that x = -4. |
Algebra Tiles--Expressions and Equations |
|
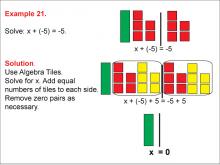
Math Example: Algebra Tiles: Example 21 | Math Example: Algebra Tiles: Example 21TopicNumerical and Algebraic Expressions DescriptionThis example demonstrates solving the equation x+(-5) = -5 using algebra tiles. The image depicts green tiles representing the variable x, red tiles representing negative integers, and yellow tiles representing positive integers. By manipulating these tiles, students can visually see that x = 0. |
Algebra Tiles--Expressions and Equations |