
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 9: Linear Models
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Quizlet Flash Cards: Evaluating Linear Functions, Set 10 | Description Evaluate linear functions of the form f(x) = ax + b in this 20-flash card set. The values of a and b are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Applications of Linear Functions |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 01 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 02 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 03 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 04 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 05 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 06 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 07 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 08 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 09 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Inverse Linear Functions, Set 10 | Description In this set of interactive flash cards, find the inverse of a given linear function. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Functions and Their Inverses |

|
Quizlet Flash Cards: Point-Slope Form | In this set of Quizlet flash cards test understanding of the point-slope form. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete Quizlet Flash Card Library, click on this link: https://media4math.com/Quizlet-Resources |
Point-Slope Form |

|
Quizlet Flash Cards: Slope-Intercept Form | In this set of Quizlet flash cards test understanding of the slope-intercept form. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete Quizlet Flash Card Library, click on this link: https://media4math.com/Quizlet-Resources |
Slope-Intercept Form |

|
SAT Math Lesson Plan 1: Linear Equations and Expressions | SAT Math Lesson Plan 1: Linear Equations and Expressions Mastering linear equations is essential for success on the SAT Math test, where the Heart of Algebra category makes up approximately 35% of the exam. This comprehensive lesson guides students through solving linear equations, simplifying algebraic expressions, and understanding slope-intercept and point-slope form. Step-by-step examples help students learn how to graph equations, recognize parallel and perpendicular lines, and interpret slope and intercepts in real-world scenarios. |
Slope-Intercept Form and Solving Two-Step Equations |

|
Test Prep Interactive Quiz--Linear Functions | Test Prep Interactive Quiz--Linear Functions
This is part of a collection of self-scoring interactive math quizzes on a variety of topics. To see the complete of these quizzes, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Graphs of Linear Functions, Slope and Slope-Intercept Form |

|
TI-84 Tutorial: Linear Functions | TI-84 Tutorial: Linear Functions
In this TI-84 tutorial we show how to graph linear functions and trace their coordinates. Note: The download is a PPT file. |
Graphs of Linear Functions |
|
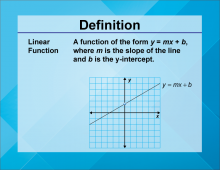
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |
|
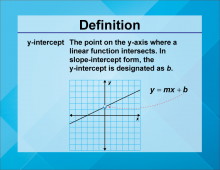
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |
|
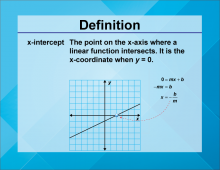
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |
|
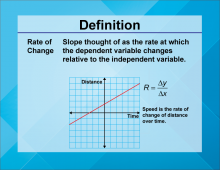
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing. |
Slope-Intercept Form |
|
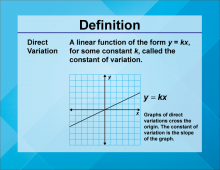
Video Definition 17--Linear Function Concepts--Direct Variation | Video Definition 17--Linear Function Concepts--Direct Variation
TopicLinear Functions DescriptionThe term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics. |
Slope-Intercept Form |
|
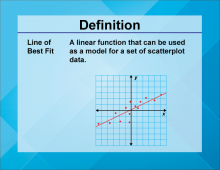
Video Definition 18--Linear Function Concepts--Line of Best Fit | Video Definition 18--Linear Function Concepts--Line of Best Fit
TopicLinear Functions DescriptionThe term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends. |
Graphs of Linear Functions |
|
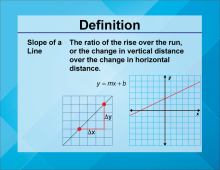
Video Definition 19--Linear Function Concepts--Slope | Video Definition 19--Linear Function Concepts--Slope
TopicLinear Functions DescriptionThe term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction. |
Slope |
|
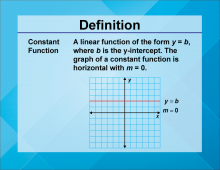
Video Definition 2--Linear Function Concepts--Constant Function | Video Definition 2--Linear Function Concepts--Constant Function
TopicLinear Functions DescriptionThe term is "Constant Function," defined as a linear function of the form y = b, where b is the y-intercept. The graph of a constant function is horizontal with a slope of m = 0. An example graph is shown with a horizontal line at y = b. This term demonstrates a special case of linear functions, emphasizing the role of constant values and their graphical representation as horizontal lines. |
Slope-Intercept Form |

|
Video Definition 20--Linear Function Concepts--System of Linear Equations | Video Definition 20--Linear Function Concepts--System of Linear Equations
TopicLinear Functions DescriptionThe term is "System of Linear Equations," defined as a collection of linear equations where the number of equations matches the number of variables, allowing for an algebraic solution. Examples include 2-variable and 3-variable systems. This term introduces the concept of interacting linear equations, paving the way for multi-variable problem-solving. |
Applications of Linear Functions and Graphs of Linear Functions |

|
Video Definition 21--Linear Function Concepts--Solution to a Linear Equation | Video Definition 21--Linear Function Concepts--Solution to a Linear Equation
TopicLinear Functions DescriptionThe term is "Solution to a Linear Equation," defined as finding the value(s) of a variable that make the equation true. An example includes solving 2x + 5 = 15 step-by-step to find x = 5. This term explains how linear equations are solved, demonstrating the logical process of isolating variables. |
Solving Systems of Equations |

|
Video Definition 22--Linear Function Concepts--Proportional Relationship | Video Definition 22--Linear Function Concepts--Proportional Relationship
TopicLinear Functions DescriptionThe term is "Proportional Relationship," defined as a type of linear relationship where two variables maintain a constant ratio. Represented as y = kx, where k is the constant ratio. This term establishes the foundation for understanding direct variation and proportionality in linear relationships. |
Proportions |
|
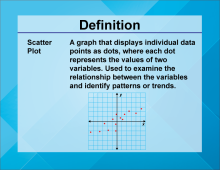
Video Definition 23--Linear Function Concepts--Scatter Plot | Video Definition 23--Linear Function Concepts--Scatter Plot
TopicLinear Functions DescriptionThe term is "Scatter Plot," defined as a graph displaying individual data points as dots, where each dot represents the values of two variables. Used to examine relationships and identify patterns or trends. This term provides a graphical tool to visualize and analyze linear relationships in data. |
Data Analysis |

|
Video Definition 24--Linear Function Concepts--Least Squares Regression Line | Video Definition 24--Linear Function Concepts--Least Squares Regression Line
TopicLinear Functions DescriptionThe term is "Least Squares Regression Line," defined as the best fit to a set of data points on a scatter plot. It minimizes the sum of the squares of the vertical distances between the data points and the line. This term links linear functions to data analysis, providing a method to model relationships in data. |
Data Analysis |
|
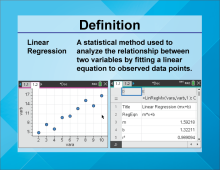
Video Definition 25--Linear Function Concepts--Linear Regression | Video Definition 25--Linear Function Concepts--Linear Regression
TopicLinear Functions DescriptionThe term is "Linear Regression," defined as a statistical method used to analyze the relationship between two variables by fitting a linear equation to observed data points. An example includes using LinReg to calculate slope (m), intercept (b), and r-squared values. This term links linear functions with statistical applications, particularly in modeling and predictions based on data. |
Data Analysis |

|
Video Definition 26--Linear Function Concepts--Correlation Coefficient | Video Definition 26--Linear Function Concepts--Correlation Coefficient
TopicLinear Functions DescriptionThe term is "Correlation Coefficient," defined as a numerical measure quantifying the strength and direction of the linear relationship between two variables, ranging from -1 to 1. A scatterplot and calculation examples are provided to illustrate this concept. This term connects linear functions to data analysis, showing how linear relationships are quantified in statistics. |
Data Analysis |

|
Video Definition 27--Linear Function Concepts--Linear Expression | Video Definition 27--Linear Function Concepts--Linear Expression
TopicLinear Functions DescriptionThe term is "Linear Expression," defined as an algebraic expression consisting of at least one term where the variable has an exponent of 1. Examples include x, 2x - 3, and -4x + 8. This term establishes the foundation of linear algebra by focusing on the simplest forms of linear relationships. |
Variable Expressions |

|
Video Definition 28--Linear Function Concepts--Inverse of a Linear Function | Video Definition 28--Linear Function Concepts--Inverse of a Linear Function
TopicLinear Functions DescriptionThe term is "Inverse of a Linear Function," defined as the function f-1(x) such that its graph is the mirror image of f(x) across the line y = x. An example is f(x) = -3x + 3 and its inverse f-1(x) = -1/3 * x + 1. This term introduces the concept of function inverses, showing symmetry in linear functions. |
Functions and Their Inverses |

|
Video Definition 29--Linear Function Concepts--Piecewise Linear Functions | Video Definition 29--Linear Function Concepts--Piecewise Linear Functions
TopicLinear Functions DescriptionThe term is "Piecewise Linear Functions," defined as special functions composed of linear function segments. Examples include step functions and absolute value functions. This term extends the scope of linear functions to piecewise and segmented applications, showcasing broader versatility. |
Special Functions |
|
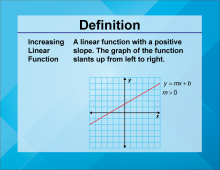
Video Definition 3--Linear Function Concepts--Increasing Linear Function | Video Definition 3--Linear Function Concepts--Increasing Linear Function
TopicLinear Functions DescriptionThe term is "Increasing Linear Function," defined as a linear function with a positive slope. The graph of the function slants up from left to right, represented as y = mx + b with m > 0. This term complements the concept of decreasing linear functions by focusing on positive slope behavior. |
Slope-Intercept Form |

|
Video Definition 30--Linear Function Concepts--Discrete Linear Functions | Video Definition 30--Linear Function Concepts--Discrete Linear Functions
TopicLinear Functions DescriptionThe term is "Discrete Linear Functions," defined as discontinuous functions made up of linear function parts. Examples include step functions, illustrated with a piecewise graph. This term extends the concept of linearity to piecewise or segmented functions, bridging the gap between continuous and discrete representations. |
Special Functions |
|
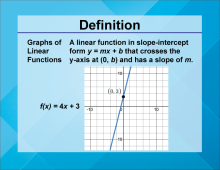
Video Definition 31--Linear Function Concepts--Graph of a Linear Function | Video Definition 31--Linear Function Concepts--Graph of a Linear Function
TopicLinear Functions DescriptionThe term is "Graphs of Linear Functions," defined as a linear function in slope-intercept form y = mx + b that crosses the y-axis at (0, b) and has a slope of m. An example graph shows f(x) = 4x + 3 crossing the y-axis at (0, 3). This term visualizes how linear functions are represented on a graph, providing insight into slope and y-intercept properties. |
Graphs of Linear Functions |

|
Video Definition 32--Linear Function Concepts--Linear Binomial | Video Definition 32--Linear Function Concepts--Linear Binomial
TopicLinear Functions DescriptionThe term is "Linear Binomial," defined as a linear polynomial consisting of two terms. Examples include x + 1, -3x + 2, and (x + 2)(x - 2) = x^2 - 4, demonstrating how linear binomials can factor into higher-order polynomials. This term builds on linear expressions by focusing on binomial cases, important for algebraic manipulation. |
Polynomial Expressions |

|
Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term | Video Definition 33--Linear Function Concepts--Coefficient of the Linear Term
TopicLinear Functions DescriptionThe term is "Coefficient of the Linear Term," defined as the numerical factor of the variable in a linear expression, equation, or function. Examples provided include x + 3, where the coefficient is 1; y = -3x + 4, where the coefficient is -3; and 7x - 6 = 15, where the coefficient is 7. This term introduces the concept of coefficients in linear expressions, forming the foundation for understanding how variables scale in linear equations. |
Variable Expressions |

|
Video Definition 34--Linear Function Concepts--Constant Term | Video Definition 34--Linear Function Concepts--Constant Term
TopicLinear Functions DescriptionThe term is "Constant Term," defined as the numerical term of a linear expression, equation, or function. Examples include x + 5, where the constant is 5; y = 5x + 2, where the constant is 2; and 3x - 2y = 10, where the constant is 10. This term explains the role of constants in linear equations, showing how they affect the y-intercept in graphing linear functions. |
Numerical Expressions |
|
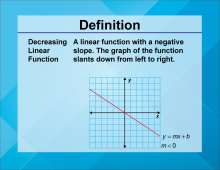
Video Definition 4--Linear Function Concepts--Decreasing Linear Function | Video Definition 4--Linear Function Concepts--Decreasing Linear Function
TopicLinear Functions DescriptionThe term is "Decreasing Linear Function," defined as a linear function with a negative slope. The graph of the function slants down from left to right, represented as y = mx + b with m < 0. This term explores a specific behavior of linear functions, illustrating how slope affects the direction of a graph. |
Slope-Intercept Form |

|
Video Definition 5--Linear Function Concepts--Identity Function | Video Definition 5--Linear Function Concepts--Identity Function
TopicLinear Functions DescriptionThe term is "Identity Function," defined as a linear function of the form y = x, where input values equal the output values. The graph is a line of slope 1. This term explains the simplest linear function and its unique property where the input equals the output. |
Slope-Intercept Form |

|
Video Definition 6--Linear Function Concepts--Slope-Intercept Form | Video Definition 6--Linear Function Concepts--Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Slope-Intercept Form," defined as the equation of a linear function written in a form that easily identifies the slope (m) and y-intercept (b). Represented as y = mx + b. This term focuses on the most common representation of linear equations, simplifying analysis and graphing. |
Slope-Intercept Form |
|
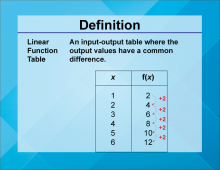
Video Definition 7--Linear Function Concepts--Linear Function Tables | Video Definition 7--Linear Function Concepts--Linear Function Tables
TopicLinear Functions DescriptionThe term is "Linear Function Table," defined as an input-output table where the output values have a common difference. An example shows a table with x-values increasing by 1 and f(x)-values increasing by 2. This term ties numerical patterns to linear functions, highlighting their consistent rate of change. |
Applications of Linear Functions and Graphs of Linear Functions |
|
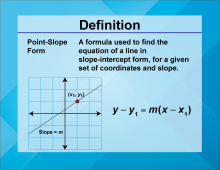
Video Definition 8--Linear Function Concepts--Point-Slope Form | Video Definition 8--Linear Function Concepts--Point-Slope Form
TopicLinear Functions DescriptionThe term is "Point-Slope Form," defined as a formula used to find the equation of a line in slope-intercept form for a given set of coordinates and slope. The formula is y - y1 = m(x - x1). This term provides a useful tool for transitioning between graph-based data and algebraic representations of linear functions. |
Point-Slope Form |

|
Video Definition 9--Linear Function Concepts--The Equation of a Line From Two Coordinates | Video Definition 9--Linear Function Concepts--The Equation of a Line From Two Coordinates
TopicLinear Functions DescriptionThe term is "The Equation of a Line from Two Coordinates," defined as deriving the equation of a line in slope-intercept form from two given points. The slope is calculated as m = (y2 - y1) / (x2 - x1), and the equation is written as y - y1 = m(x - x1). This term builds the connection between points on a graph and their corresponding linear equation, demonstrating practical derivations. |
Point-Slope Form |