
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 9: Linear Models
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
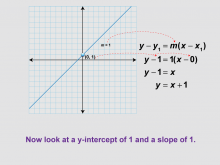
Math Clip Art--Linear Functions Concepts--Point-Slope Form 8 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 8TopicLinear Functions DescriptionThis image presents a variation of the previous example, now with the coordinate (0, 1) and a slope of 1. It demonstrates how to use the point-slope form when the y-intercept is not at the origin. By incorporating this visual aid, teachers can help students understand how the point-slope form can be used with different y-intercepts. This image is particularly useful for showing how the form adapts to different scenarios while maintaining its basic structure. |
Graphs of Linear Functions and Slope-Intercept Form |
|
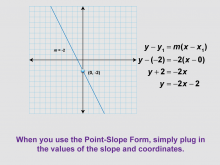
Math Clip Art--Linear Functions Concepts--Point-Slope Form 9 | Math Clip Art--Linear Functions Concepts--Point-Slope Form 9TopicLinear Functions DescriptionThis image shows a variation of the previous example, now with a line having a negative slope of -2 and crossing the y-axis at (0, -2). It demonstrates how to use the point-slope form with negative slopes and y-intercepts. By using this visual aid, teachers can help students understand how the point-slope form accommodates negative values. This image is particularly useful for expanding students' understanding of the form's versatility. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 1 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 1TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + 1, where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 10 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 10TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 9x + (-2), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 2 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 2TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 6x + (-10), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 3 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 3TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -x + (-8), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 4 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 4TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 5 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 5TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -6x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 6 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 6TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -3x + 1, where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 7 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 7TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = -10x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 8 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 8TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + (-9), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 9 | Math Example--Linear Function Concepts--Evaluating Linear Functions: Example 9TopicLinear Functions DescriptionThis example demonstrates how to evaluate a linear function at a specific value. The function in this example is the function f(x) = 7x + (-3), where x is replaced with a given value to determine the corresponding f(x) value. The process includes substitution and arithmetic simplification. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x + y = 1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x + 1. This simple transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x - 1. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y and changing the sign of both sides, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -x + y = 1 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = -1 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation -x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y, resulting in y = -x - 1. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. Linear functions are fundamental mathematical concepts that describe relationships between two variables. The examples in this collection, such as showing step-by-step transformations from standard form to slope-intercept form, help in understanding how each part of the equation affects the graph and the relationship itself. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x - y = -1 from standard form to slope-intercept form. The solution involves isolating y, resulting in y = x + 1. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = 1 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = -x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 12x + 28y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -3/7 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 3x + 6y = -18 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -1/2 x - 3. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -14x - 35y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = -2/5 x. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 28x - 21y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 4/3 x. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation -13x + 39y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = 1/3 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 5x - 2y = 12 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 2.5x - 6. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -6x + 10y = 20 from standard form to slope-intercept form. The solution process involves isolating y and dividing by its coefficient, resulting in y = 0.6x + 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -9x - 15y = -45 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = 3/5 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -8x - 12y = 25 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -2/3 x - 25/12. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7TopicLinear Functions DescriptionThis example illustrates the transformation of the linear equation -2x + 16y = -36 from standard form to slope-intercept form. The solution process involves solving for y, resulting in y = 1/8 x - 9/4. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8TopicLinear Functions DescriptionThis example showcases the conversion of the linear equation -7x + 21y = 63 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = 1/3 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9TopicLinear Functions DescriptionThis example demonstrates the process of converting the linear equation 10x - 28y = 56 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = (5/14)x - 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 1 | Math Example--Linear Function Concepts--Linear Function Machines--Example 1TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 2x. This involves creating a table of values for x and f(x) using f(x) = 2x. The output for each x is calculated by multiplying x by 2. The results are f(x) = -4, -2, 0, 2, and 4 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 10 | Math Example--Linear Function Concepts--Linear Function Machines--Example 10TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x + 1. This involves creating a table of values for x and f(x) using f(x) = 3x + 1. The output for each x is calculated by tripling x and then adding 1. The results are f(x) = -5, -2, 1, 4, and 7 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 11 | Math Example--Linear Function Concepts--Linear Function Machines--Example 11TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 4 * x + 1. This involves a table created for x and f(x) values. By substituting each x value into f(x) = 4 * x + 1, the outputs are calculated as follows: -2 gives -7, -1 gives -3, 0 gives 1, 1 gives 5, and 2 gives 9. The common difference between successive outputs is +4, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 12 | Math Example--Linear Function Concepts--Linear Function Machines--Example 12TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = 5 * x + 1. This involves a table created for x and f(x) values. substituting each x into f(x) = 5 * x + 1, the outputs are calculated: -2 gives -9, -1 gives -4, 0 gives 1, 1 gives 6, and 2 gives 11. the common difference between outputs is +5, confirming a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
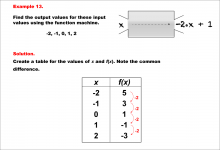
Math Example--Linear Function Concepts--Linear Function Machines--Example 13 | Math Example--Linear Function Concepts--Linear Function Machines--Example 13TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -2 * x + 1. This involves a table created for x and f(x) values. Substituting each x into f(x) = -2 * x + 1, the outputs are: -2 gives 5, -1 gives 3, 0 gives 1, 1 gives -1, and 2 gives -3. The common difference is -2, indicating a linear function. |
Graphs of Linear Functions and Slope-Intercept Form |
|
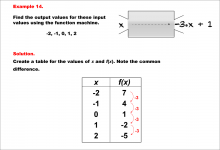
Math Example--Linear Function Concepts--Linear Function Machines--Example 14 | Math Example--Linear Function Concepts--Linear Function Machines--Example 14TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -3 * x + 1. This involves a table created for x and f(x) values. Each x substituted into f(x) = -3 * x + 1 yields: -2 gives 7, -1 gives 4, 0 gives 1, 1 gives -2, and 2 gives -5. The common difference is -3, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |
|
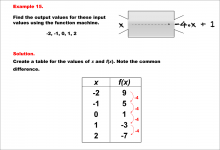
Math Example--Linear Function Concepts--Linear Function Machines--Example 15 | Math Example--Linear Function Concepts--Linear Function Machines--Example 15TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -4 * x + 1. This involves a table is created for x and f(x) values. Calculating for each x: -2 gives 9, -1 gives 5, 0 gives 1, 1 gives -3, and 2 gives -7. The common difference is -4, indicating linearity. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |
|
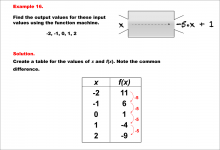
Math Example--Linear Function Concepts--Linear Function Machines--Example 16 | Math Example--Linear Function Concepts--Linear Function Machines--Example 16TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the equation f(x) = -5 * x + 1. This involves a table created for x and f(x) values. Substituting into f(x) = -5 * x + 1, the outputs are: -2 gives 11, -1 gives 6, 0 gives 1, 1 gives -4, and 2 gives -9. The common difference is -5, confirming linearity. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 17 | Math Example--Linear Function Concepts--Linear Function Machines--Example 17TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 2. This involves a table created for x and f(x) values, where f(x) = 2 for all x values, resulting in outputs of 2, 2, 2, 2, and 2. The common difference is 0, indicating a constant function: y = 2. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 18 | Math Example--Linear Function Concepts--Linear Function Machines--Example 18TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = 0. This involves a table created for x and f(x) values, where f(x) = 0 for all x values, giving outputs of 0, 0, 0, 0, and 0. The common difference is 0, indicating a constant function: y = 0. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 19 | Math Example--Linear Function Concepts--Linear Function Machines--Example 19TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using the function machine represented by the constant function f(x) = -1. This involves a table created for x and f(x) values, where f(x) = -1 for all x values, resulting in outputs of -1, -1, -1, -1, and -1. The common difference is 0, indicating a constant function: y = -1. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 2 | Math Example--Linear Function Concepts--Linear Function Machines--Example 2TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 3x. This involves creating a table of values for x and f(x) using f(x) = 3x. The output for each x is calculated by multiplying x by 3. the results are f(x) = -6, -3, 0, 3, and 6 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 3 | Math Example--Linear Function Concepts--Linear Function Machines--Example 3TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 4x. This involves creating a table of values for x and f(x) using f(x) = 4x. The output for each x is calculated by multiplying x by 4. The results are f(x) = -8, -4, 0, 4, and 8 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 4 | Math Example--Linear Function Concepts--Linear Function Machines--Example 4TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = 5x. This involves creating a table of values for x and f(x) using f(x) = 5x. The output for each x is calculated by multiplying x by 5. The results are f(x) = -10, -5, 0, 5, and 10 for x = -2, -1, 0, 1, and 2, respectively. Linear Functions are a key concept in mathematics that involves understanding the relationship between input and output values based on a given rule. Examples like this one help students visualize and analyze patterns, making it easier to comprehend linear relationships. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 5 | Math Example--Linear Function Concepts--Linear Function Machines--Example 5TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -2x. This involves creating a table of values for x and f(x) using f(x) = -2x. The output for each x is calculated by multiplying x by -2. The results are f(x) = 4, 2, 0, -2, and -4 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Function Machines--Example 6 | Math Example--Linear Function Concepts--Linear Function Machines--Example 6TopicLinear Functions DescriptionFind the output values for the input values -2, -1, 0, 1, 2 using a function machine with the rule f(x) = -3x. This involves creating a table of values for x and f(x) using f(x) = -3x. The output for each x is calculated by multiplying x by -3. The results are f(x) = 6, 3, 0, -3, and -6 for x = -2, -1, 0, 1, and 2, respectively. |
Graphs of Linear Functions and Slope-Intercept Form |