Lesson Plan: Graphing and Interpreting Proportional Relationships

Lesson Objectives

This lesson can be completed in one 50-minute class period. 

• Graph proportional relationships
• Interpret the unit rate as the slope of a graph
• Compare two different proportional relationships using graphs
• Explain the meaning of points on a proportional relationship graph
• Analyze real-world data to understand relationships in various contexts

Common Core Standards

CCSS.MATH.CONTENT.7.RP.A.2.A
Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.

CCSS.MATH.CONTENT.7.RP.A.2.D
Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.

CCSS.MATH.CONTENT.8.EE.B.5
Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.

Prerequisite Skills

• Plotting points on a coordinate plane
• Understanding of unit rate

Key Vocabulary

• Slope
• Origin
• Linear relationship
• Coordinate plane

Warm-up Activity (10 minutes)

Present students with the following data table showing hours worked and total pay for a part-time job:

Ask students to:

1. Plot these points on a coordinate plane
2. Determine if they form a straight line through the origin
3. Calculate the hourly wage (slope of the line)

Use this Desmos activity:

https://www.desmos.com/calculator/utzva5dltc

Teach (25 minutes)

Definitions

• Proportional Relationship: A relationship between two quantities where one quantity is a constant multiple of the other.
• Slope: The steepness of a line, calculated as the change in y divided by the change in x.
• Unit Rate: The rate per one unit of the independent variable.
• Origin: The point (0,0) on a coordinate plane.
• Linear Relationship: A relationship that forms a straight line when graphed.
• Coordinate Plane: A two-dimensional plane using x and y axes to determine the position of points.

Use this slide show to review these and other definitions:

https://www.media4math.com/library/slideshow/definitions-graphing-and-interpreting-proportional-relationships

Instruction

Demonstrate how to graph proportional relationships, explain how the unit rate relates to the slope of the graph, and show how to compare different proportional relationships using graphs.

Example 1: Graphing a Cell Phone Plan

A cell phone plan charges $0.10 per minute of talk time.

• Create a table of values for minutes used and cost.
• Graph the relationship.
• Identify the unit rate and explain its meaning in context.

Solution:

Graph: A straight line passing through these points and the origin.

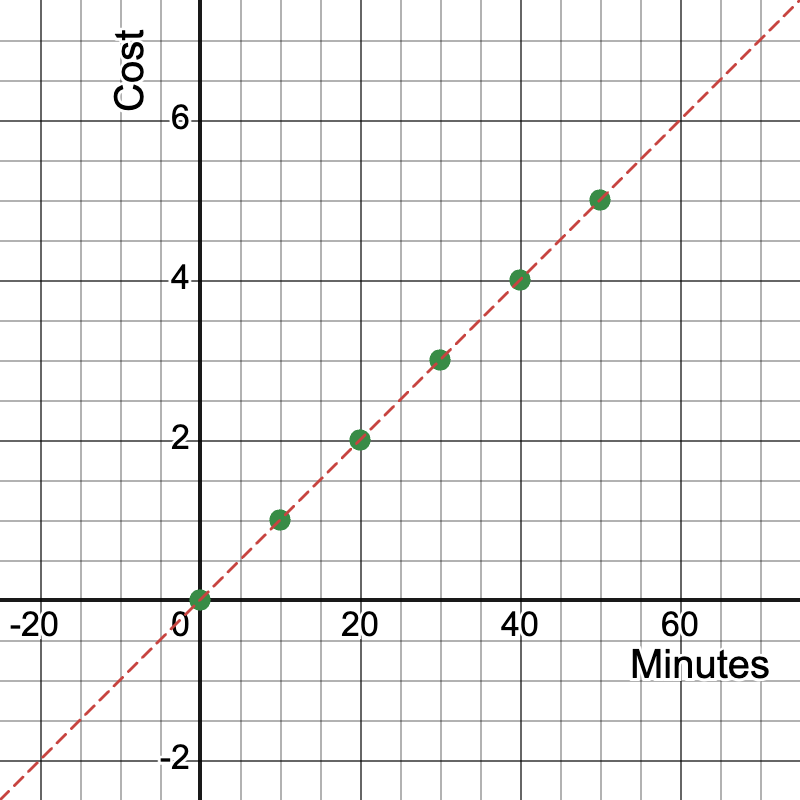
Unit rate: $0.10 per minute, represented by the slope of the line.
Slope calculation: Slope = (y2 - y1) / (x2 - x1) = (5 - 0) / (50 - 0) = 5/50 = 0.10

Use this Desmos activity:

https://www.desmos.com/calculator/kamtpaelpc 

Example 2: Comparing Running Speeds

Runner A covers 6 miles in 1 hour. 

Runner B covers 10 miles in 2 hours.

• Create a table of values for both runners.
• Graph both relationships on the same coordinate plane.
• Compare the speeds of the two runners.

Solution:

Graph: Plot both sets of points on the same coordinate plane.

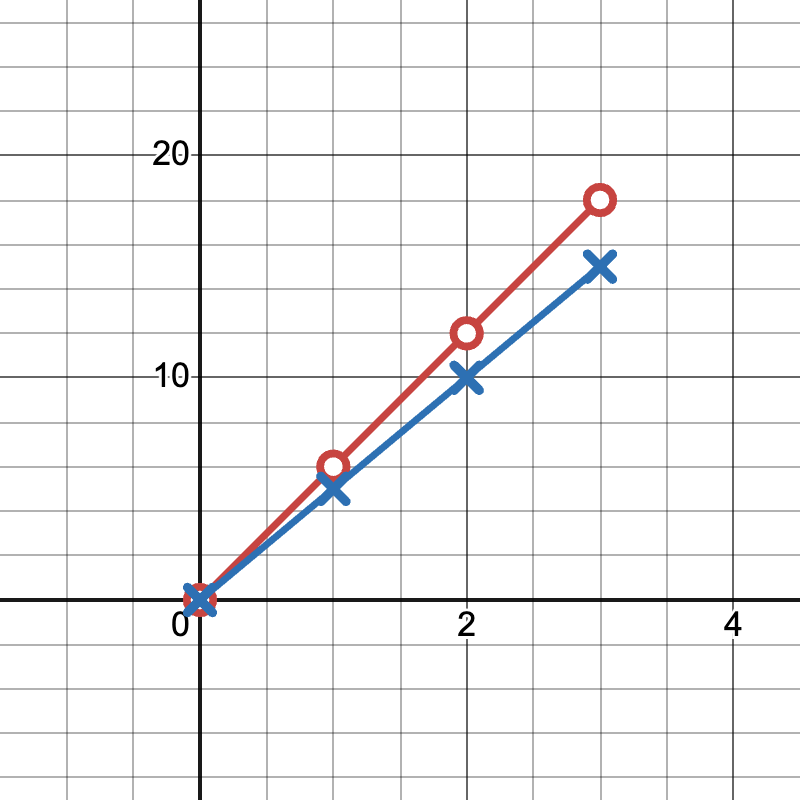
Runner A's line is y = 6x, Runner B's line is y = 5x
Runner A is faster as their line has a steeper slope (6 vs 5).

Use this Desmos activity:

https://www.desmos.com/calculator/owuxtaevo1

Example 3: Sales Growth in a Startup Business

A tech startup's monthly revenue growth is shown in the following data:

• Graph this relationship on a coordinate plane.
• What does the point (3, 60) represent?
• What is the meaning of the slope in this context?

Solution:

• Graph: A straight line passing through these points and the origin.
   

  

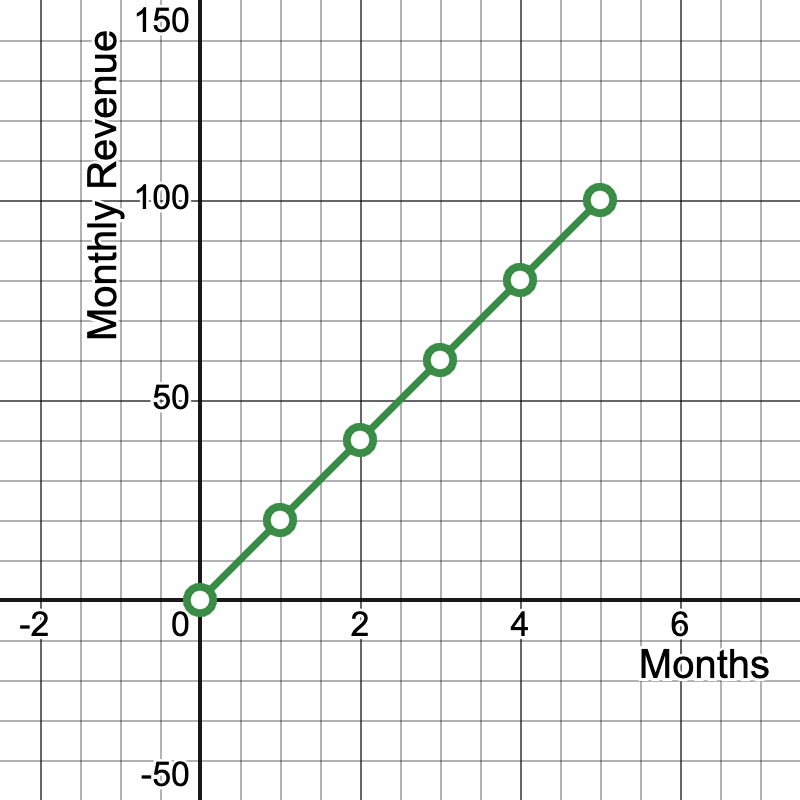
• The point (3, 60) represents that after 3 months since launch, the company's monthly revenue was $60,000.
• Slope calculation: Slope = (100 - 0) / (5 - 0) = 20
• The slope of 20 means the company's revenue is growing by $20,000 per month.
• This linear relationship indicates a consistent growth rate, which is a positive sign for the startup.

Use this Desmos activity:

https://www.desmos.com/calculator/pmft2bgx4q

Example 4: Education and Income Relationship

Let's examine the relationship between years of education and median weekly earnings using real data from the U.S. Bureau of Labor Statistics (2020):

• Graph this relationship on a coordinate plane.
• What does the point (16, 1305) represent?
• Is this a proportional relationship? Why or why not?

Solution:

• Graph: Plot the points on a coordinate plane. The resulting line will not pass through the origin. (Note: The graph is a linear regression line.)
   

  

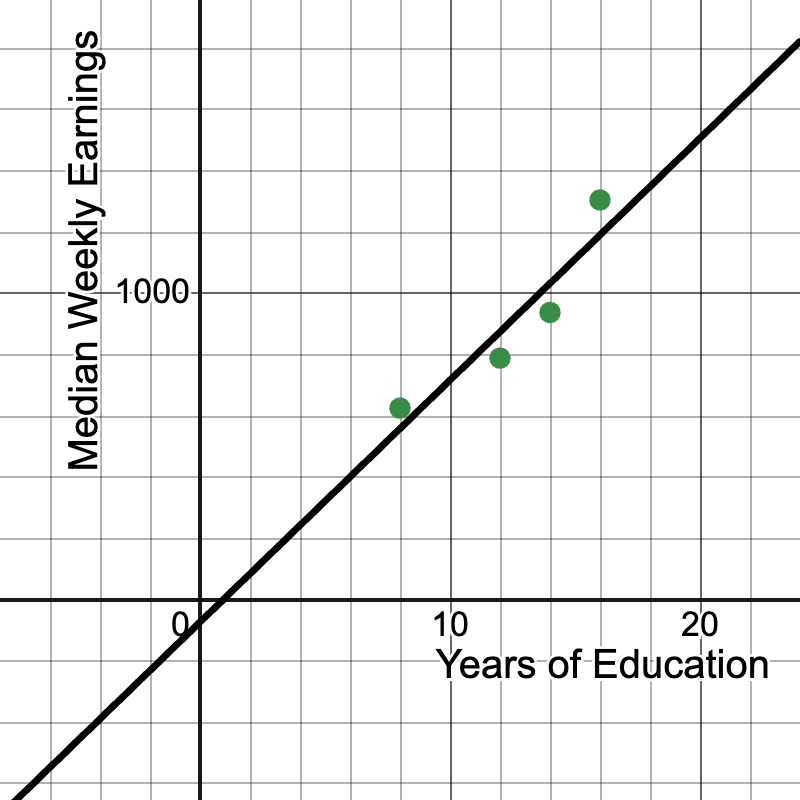
• The point (16, 1305) represents that individuals with 16 years of education (typically a bachelor's degree) had median weekly earnings of $1,305.
• This is not a proportional relationship because:
  1. The graph does not pass through the origin (0, 0).
  2. The rate of change (slope) is not constant between all points.
  3. The range of this graph would be for x ≥ 0, since it makes no sense that 0 years of education resulting in any earnings.
• However, there is a clear positive correlation between years of education and median weekly earnings.
• We can calculate the average rate of change: Slope = (1305 - 626) / (16 - 8) = 679 / 8 ≈ 84.88 This means that, on average, each additional year of education is associated with an increase of about $84.88 in median weekly earnings.

Use this Desmos activity, which includes a regression line:

https://www.desmos.com/calculator/q2gs51jf5f 

Review (10 minutes)

Group activity: Students analyze and graph real-world data from arts, technology, and sports. Use this slide show to support the following three examples, which include data sets and lines of best fit. The slope as a unit rate can potentially be used to make predictions:

https://www.media4math.com/library/slideshow/applications-proportional-reasoning-linear-graphs

Example 1. Arts: Broadway Show Ticket Prices (2010-2019)

This data set shows the changing price of Broadway theater ticket prices. 

Data from The Broadway League:

Students graph this data and interpret the slope as the average yearly increase in ticket prices. Here is a Desmos activity you can use as a companion to this review activity. Note that it includes a line of best fit, which you can briefly explain to students:

https://www.desmos.com/calculator/mc1y6t4jwe

Example 2. Technology: Global Smartphone Sales (2016-2019)

This data set on Smartphone sales can be used to generate a line of best fit. 

Data from Statista:

Students graph this data and discuss why this relationship might not be proportional. Use this Desmos activity, which includes a regression line. Discuss the advantages and disadvantages of this linear model:

https://www.desmos.com/calculator/t6nctgqhcp 

Example 3. Sports: NBA Player Height vs. Points per Game (2020-2021 season)

This data set looks at the relationship between height and average points per game for NBA players.

Data from NBA statistics:

Students graph this data and interpret the slope as the average increase in points scored per inch of height. Here is a Desmos activity to use:

https://www.desmos.com/calculator/1hsko7f67q

Assess (5 minutes)

Administer this 10-question quiz.

Quiz

1. Graph the proportional relationship y = 3x. What is the slope of this line?
   
    
2. If a line passes through the points (0,0) and (4,12), what is the unit rate?
   
    
3. Compare the steepness of y = 2x and y = 0.5x. Which has a greater rate of change?
   
    
4. What does the point (1, 5) represent on a graph of a proportional relationship?
   
    
5. Graph y = 4x and y = 2x on the same coordinate plane. How do they compare?
   
    
6. If a car travels 240 miles in 4 hours at a constant speed, what is the slope?
   
    
7. Does the graph of y = 3x + 2 represent a proportional relationship? Why or why not?
   
    
8. On a graph of distance vs. time for a constant speed, what does the slope represent?
   
    
9. If two people are running at different constant speeds, how would their distance-time graphs compare?
   
    
10. What is the y-intercept of all proportional relationships when graphed?
    
     

Answer Key

1. 3
2. 3
3. y = 2x has a greater rate of change
4. For every 1 unit of x, y increases by 5 units
5. y = 4x has a steeper slope
6. Slope is 60 (miles per hour)
7. No, because it doesn't pass through (0,0)
8. Speed or velocity
9. Different slopes, steeper slope indicates faster speed
10. (0,0)

Purchase the lesson plan bundle. Click here.