Lesson Plan: Graphing Linear Equations

Lesson Objectives:

  • Graph linear equations using various methods
  • Use slope-intercept form
  • Use x and y intercepts
  • Interpret slope and y-intercept in real-world contexts

Florida BEST Standards:

  • MA.8.AR.2.1: Recognize slope and y-intercept in y = mx + b; interpret in real-world context.
  • MA.8.AR.2.3: Determine slope from table, graph, or description.
  • MA.8.AR.3.2: Write equation in slope-intercept form from table, graph, or description.
  • MA.8.AR.3.4: Determine and interpret rate of change as slope.
  • MA.8.AR.3.5: Solve real-world problems with linear equations in two variables.
  • MA.8.F.1.1: Determine if a relation is a function; identify domain and range.
  • MA.8.F.1.2: Determine if a function is linear from graph, equation, or table.

Prerequisite Skills:

  • Plotting points on the coordinate plane
  • Understanding of slope and y-intercept concepts

Key Vocabulary:

  • Coordinate plane
  • Ordered pair
  • Slope
  • y-intercept
  • Slope-intercept form

Warm-up Activity (5 minutes)

For students that need to review graphing points on the coordinate plane review the first example from this video:

https://www.media4math.com/library/39514/asset-preview

Engage students by asking them to plot the following points on a coordinate plane: 

(1, 2)

(2, 4)

(3, 6). 

Use this Desmos activity to graph the points and ask students to notice any patterns. 

https://www.desmos.com/calculator/cq834lfyfp

Then ask them to find additional coordinates that continue the pattern.

Teach (20 minutes)

Definitions

Use the following video definitions to define key terms:

Examples

Demonstrate how to identify the slope and y-intercept from a given linear equation.

Review (10 minutes)

Assess (10 minutes)

Administer a 10-question quiz to assess students' understanding of graphing linear equations. The quiz should include questions on plotting points, identifying slope and y-intercept, graphing linear equations, and interpreting slope and y-intercept in real-life situations.

Quiz

  1. Plot the points (1, 2), (-2, -1), and (3, 4) on the coordinate plane.
    Coordinate grid

     
  2. Identify the slope and y-intercept of the equation y = 2x + 3.

     
  3. Graph the equation y = -1/2x + 4 on the coordinate plane.
    Coordinate grid

     
  4. If the slope of a linear equation is 3 and the y-intercept is -2, what is the equation?

     
  5. Interpret the meaning of the slope and y-intercept in the equation y = 0.5x + 10. You save fifty cents a day in a piggy bank that already has an amount of money in it.

     
  6. A line passes through the origin and through (4, 9). What is its equation?

     
  7. Determine if the point (3, -1) lies on the line represented by the equation y = 2x - 5.

     
  8. Graph the equation 3y = 6x - 9 on the coordinate plane.
    Coordinate grid

     
  9. Explain the relationship between the slope of a line and its steepness.

     
  10. This equation represents a car slowing down every second at a constant speed (in miles per hour): y = -5x +50. What is the car's initial speed? What does the slope represent?

     

Answer Key

  1. Coordinate grid
  2. Slope = 2, y-intercept = 3
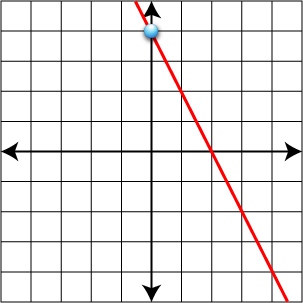
  3. Linear graph
  4. y = 3x - 2
  5. The slope represents the 50 cents saved a day. The y-intercept is the amount of money initially in the piggy bank (\$10).
  6. y = 9/4x
  7. No, the point (3, -1) does not lie on the line.
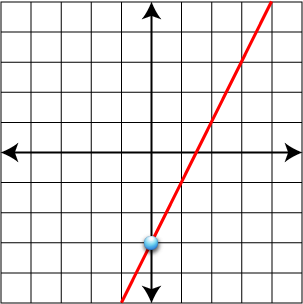
  8. Linear graph
  9. The steeper the line, the greater the slope value (positive or negative).
  10. Initial speed is 50 mph. The car slows down by 5 mph every second.

 

Purchase the lesson plan bundle. Click here.