 Lesson Plan: Linear Inequalities
Lesson Plan: Linear Inequalities
Lesson Objectives
- Represent inequalities on a number line
- Solve inequalities algebraically
- Graph solutions of inequalities
- Apply linear inequalities to real-world situations
Florida BEST Standards
- MA.8.AR.2.4: Graph inequalities on a number line in context.
- MA.8.AR.2.5: Solve one-variable inequalities; represent solutions algebraically and graphically.
- MA.8.AR.3.5: Solve real-world problems with linear equations in two variables.
- MA.7.AR.2.2: Write and solve two-step equations in one variable with rational numbers.
Prerequisite Skills
- Understanding of linear equations
- Graphing linear equations
- Solving linear equations algebraically
Key Vocabulary
- Linear inequality
- Solution set
- Inequality symbol (≤, ≥, <, >)
- Boundary line
Warm-up Activity (10 minutes)
Introduce the concept of inequalities by asking students to compare two quantities using inequality symbols (e.g., 5 < 7, 10 ≥ 8). Discuss how inequalities are different from equations and how they represent a range of values rather than a single value.
Use this slide show to go over math examples of inequalities in one variable graphed on a number line:
https://www.media4math.com/library/slideshow/math-examples-one-variable-inequalities
Teach (20 minutes)
Introduction to Linear Inequalities
Use this slide show to review these definitions of inequalities:
https://www.media4math.com/library/slideshow/definitions-inequalities
Provide examples of linear inequalities and discuss their meaning (e.g., 2x + 3 ≤ 7 means that the value of 2x + 3 must be less than or equal to 7).
Graphing Linear Inequalities
Demonstrate how to graph a linear inequality on the coordinate plane by graphing the boundary line and shading the appropriate region. Emphasize the importance of the inequality symbol in determining which region to shade.
Use this selection of clip art images to show the contrast between equations and inequalities with one and two variables:
https://www.media4math.com/library/75525/asset-preview
Use this Desmos activity to explore graphs of linear inequalities:
https://www.desmos.com/calculator/vhqsry1h6b
Use this slide show to look at examples of graphs of linear inequalities:
https://www.media4math.com/library/slideshow/math-examples-linear-inequalities
Solving Linear Inequalities Algebraically
Introduce the process of solving linear inequalities algebraically, similar to solving linear equations. Emphasize the importance of reversing the inequality symbol when multiplying or dividing by a negative number.
Use this slide show to demonstrate how to solve one-step inequalities algebraically:
https://www.media4math.com/library/slideshow/solving-one-step-inequalities
Use this set of math clip art images to demonstrate how to solve linear inequalities:
https://www.media4math.com/library/75527/asset-preview
Review (5 minutes)
Review the key concepts covered in the lesson, including the definition of linear inequalities, graphing linear inequalities, and solving linear inequalities algebraically.
Use this video to see an application of linear inequalities in the context of business:
https://www.media4math.com/library/39668/asset-preview
The first few minutes of this video sets up the scenario and you will see the resulting inequality:
y > -2/3x + 20
While the video shows how to graph this inequality on a TI-Nspire graphing calculator, you can also use Desmos.
Assess (10 minutes)
Administer the following quiz.
Quiz
- Graph the linear inequality: 2x - 3y ≥ 6
- Solve the linear inequality: 4x + 2y < 10
- Which of the following points does not satisfy the inequality 3x - 2y ≤ 12?
a) (2, 3)
b) (5, 1)
c) (1, 4)
d) (3, 2)
- Write an inequality to represent the situation: The cost of a movie ticket is \$8 for adults and \$6 for children, and you have \$50 to spend. What combination of tickets can you purchase?
- Graph the linear inequality: y ≥ 2x - 4

- Which of the following points does not satisfy the inequality 2x + y ≤ 6?
a) (1, 2)
b) (2, 0)
c) (0, 4)
d) (3, 1)
Answer Key
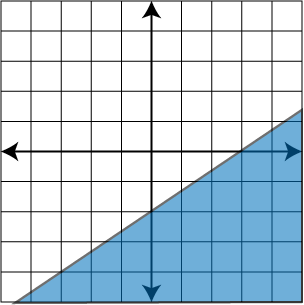
- y < -2x + 5
- b
- 8x + 6y ≤ 50
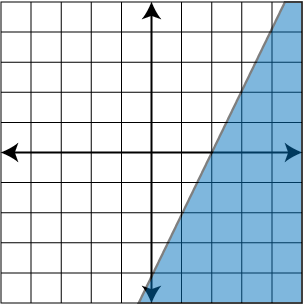
- d
![]() Purchase the lesson plan bundle. Click here.
Purchase the lesson plan bundle. Click here.